Всем привет! Меня зовут Гриша и я основатель CGDevs. Сегодня мне бы хотелось продолжить тему математики в разработке игр.
В предыдущая статья Были показаны базовые примеры использования векторов и интегралов в проектах Unity, а теперь поговорим о матрицах и аффинных преобразованиях.
Если вы хорошо разбираетесь в матричной арифметике; знать, что такое TRS и как с ним работать; Что такое трансформация Домохозяина? Возможно, вы не найдете для себя ничего нового.
Мы будем говорить в контексте 3D-графики.
Если вам интересна эта тема, добро пожаловать под кат. 
Начнем с одного из самых важных понятий в контексте статьи – аффинные преобразования .
Аффинные преобразования По сути, это преобразование системы координат (или пространства) путем умножения вектора на специальную матрицу.
Например, такие преобразования, как движение, вращение, масштабирование, отражение и т. д. Основные свойства аффинных преобразований заключаются в том, что вы остаетесь в том же пространстве (невозможно сделать двумерный вектор из трехмерного) и что если до трансформации линии пересекались/были параллельны/пересеклись, то это свойство сохранится и после трансформации.
Кроме того, они обладают множеством математических свойств, требующих знаний теории групп, теории множеств и линейной алгебры, что упрощает работу с ними.
TRS-матрица
Вторым важным понятием компьютерной графики является TRS-матрица .С его помощью можно описать наиболее распространенные операции, используемые при работе с компьютерной графикой.
TRS-матрица представляет собой композицию трех матриц преобразования.
Матрицы перевода (Translation), вращения по каждой оси (Rotation) и масштабирования (Scale).
Она выглядит вот так.
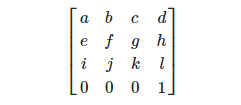
Где: Движущийся - Этот т = новый Vector3(d, h, l).
Масштабирование – с = новый Vector3(новый Vector3(a, e, i).
величина, новый Vector3(b, f, j).
величина, новый Vector3(c, g, k).
величина); Повернуть представляет собой матрицу вида: 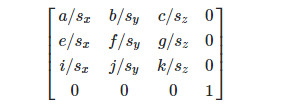
Теперь давайте немного углубимся в контекст Unity. Начнем с того, что матрица TRS — вещь очень удобная, но ее не следует использовать везде.
Так как просто указать положение или добавить векторы в Unity будет работать быстрее, но во многих математических алгоритмах матрицы в разы удобнее векторов.
Функциональность TRS в Unity во многом реализована в классе Матрица4x4 , но это не удобно с точки зрения применения.
Поскольку помимо использования матрицы посредством умножения она вообще может хранить информацию об ориентации объекта, а также при некоторых преобразованиях, я хочу иметь возможность вычислять не только положение, но и менять ориентацию объекта как целое (например, отражение, которое не реализовано в Unity) Все примеры ниже приведены для локальной системы координат (началом координат является положение GameObject, внутри которого находится объект. Если объект является корнем иерархии в юните, то началом координат является мир ( 0,0,0)).
Поскольку с помощью TRS-матрицы в принципе можно описать положение объекта в пространстве, нам нужна декомпозиция из TRS на конкретные значения положения, поворота и масштаба для Unity. Для этого можно написать методы расширения класса Matrix4x4. Получение положения, вращения и масштаба
Теги: #игры #Разработка игр #математика #программирование #gamedev #gamedevelopment #C++ #unity #.public static Vector3 ExtractPosition(this Matrix4x4 matrix) {
NET #gamedev #Matrix #algorithms #matrices #unity3d #math #unity
-
Кольбе, Адольф Вильгельм Герман
19 Oct, 24 -
Кто Станет Интернет-Президентом?
19 Oct, 24 -
Еще Одно Решение Highloadcup На Go
19 Oct, 24 -
Евросеть - Консультанты Просто Вау!
19 Oct, 24 -
Тесты Производительности Ebs
19 Oct, 24


