Введение 
Я математик и программист. Самый большой скачок в моей карьере произошел, когда я научился говорить: "Я ничего не понимаю!" Теперь мне не стыдно сказать светилу науки, что он читает мне лекцию, что я не понимаю, что он, светило, мне говорит. И это очень сложно.
Да, признать свое невежество сложно и стыдно.
Кому понравится признавать, что он чего-то не знает? В силу моей профессии мне приходится посещать большое количество презентаций и лекций, на которых, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю.
Но я не понимаю, потому что огромная проблема нынешней ситуации в науке заключается в математике.
Предполагается, что все слушатели знакомы абсолютно со всеми разделами математики (что абсурдно).
Признаться в том, что вы не знаете, что такое производная (о том, что это такое, мы поговорим чуть позже), стыдно.
Но я научился говорить, что не знаю, что такое умножение.
Да, я не знаю, что такое подалгебра над алгеброй Ли.
Да, я не знаю, зачем в жизни нужны квадратные уравнения.
Кстати, если вы уверены, что знаете, то нам есть о чем поговорить! Математика — это набор трюков.
Математики пытаются запутать и запугать публику; где нет путаницы, нет репутации, нет авторитета.
Да, престижно говорить на максимально абстрактном языке, а это полная чушь.
Знаете ли вы, что такое производная? Скорее всего вы мне расскажете о пределе соотношения разностей.
На первом курсе математики и механики в СПбГУ Виктор Петрович Хавин мне определенный производная как коэффициент при первом члене ряда Тейлора функции в точке (это была отдельная гимнастика по определению ряда Тейлора без производных).
Я долго смеялся над этим определением, пока наконец не понял, о чем оно.
Производная — это не что иное, как простая мера того, насколько похожа функция, которую мы дифференцируем, на функцию y=x, y=x^2, y=x^3. Теперь я имею честь читать лекции студентам, которые испуганный математика.
Если вы боитесь математики, мы идем по тому же пути.
Как только вы попытаетесь прочитать какой-то текст и вам покажется, что он слишком сложен, то знайте, что он плохо написан.
Я утверждаю, что нет ни одной области математики, которую нельзя было бы обсуждать «на пальцах» без потери точности.
Задача на ближайшее время: Я поставил перед учениками задачу понять, что линейно-квадратичный регулятор .
Не стесняйтесь, потратьте три минуты своей жизни и перейдите по ссылке.
Если вы ничего не понимаете, то мы на одном пути.
Я (профессиональный математик-программист) тоже ничего не понял.
И уверяю вас, в этом можно разобраться «на пальцах».
На данный момент я не знаю, что это такое, но уверяю вас, что мы сможем в этом разобраться.
Итак, первая лекция, которую я собираюсь прочесть своим студентам после того, как они в ужасе прибегут ко мне и скажут, что линейно-квадратичный регулятор — это ужасная вещь, которую вы никогда в жизни не освоите: методы наименьших квадратов .
Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то, скорее всего, нет.
Итак, по двум точкам (x0, y0), (x1, y1), например (1,1) и (3,2), задача состоит в том, чтобы найти уравнение прямой, проходящей через эти две точки: иллюстрация 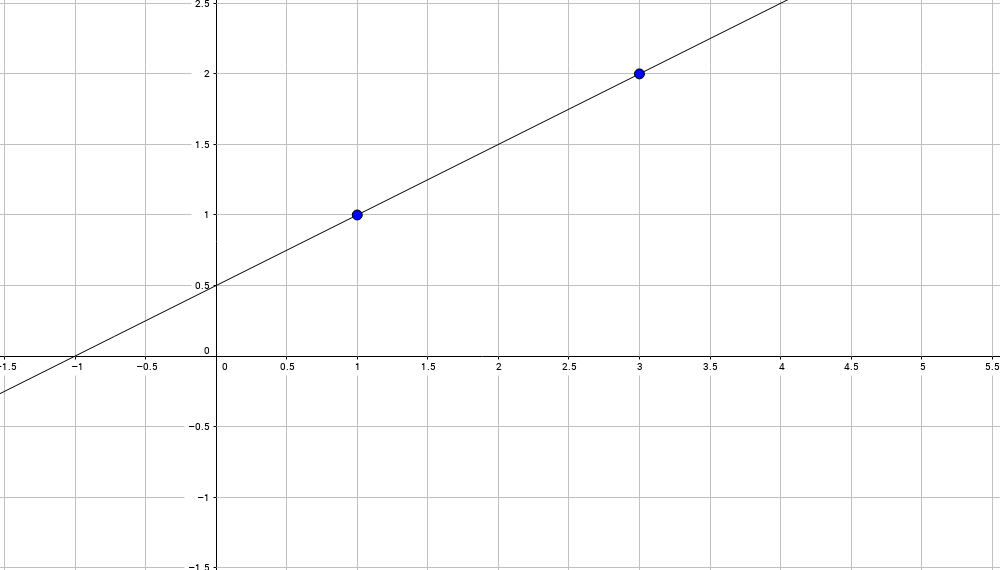
Эта строка должна иметь уравнение, подобное следующему:
Здесь альфа и бета нам неизвестны, но известны две точки этой линии:
Мы можем записать это уравнение в матричной форме:
Здесь следует сделать лирическое отступление: что такое матрица? Матрица — это не что иное, как двумерный массив.
Это способ хранения данных; к нему не следует придавать никаких дополнительных значений.
От нас зависит, как именно интерпретировать ту или иную матрицу.
Периодически я буду интерпретировать его как линейное отображение, периодически как квадратичную форму, а иногда просто как набор векторов.
Все это будет разъяснено в контексте.
Заменим конкретные матрицы их символическим представлением:
Тогда (альфа, бета) можно легко найти:
Более конкретно для наших предыдущих данных:
Что приводит к следующему уравнению линии, проходящей через точки (1,1) и (3,2):
Ладно, здесь все ясно.
Найдем уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):
Ой-ой-ой, а ведь у нас есть три уравнения с двумя неизвестными! Обычный математик скажет, что решения нет. Что скажет программист? И сначала перепишет предыдущую систему уравнений в следующем виде:
А затем попытается найти решение, минимально отклоняющееся от заданных равенств.
Назовем вектор (x0,x1,x2) вектором i, (1,1,1) вектором j и (y0,y1,y2) вектором b:
В нашем случае векторы i, j, b трехмерны, поэтому (в общем случае) решения у этой системы нет. Любой вектор (alpha\*i + beta\*j) лежит в плоскости, натянутой векторами (i, j).
Если b не принадлежит этой плоскости, то решения нет (в уравнении невозможно добиться равенства).
Что делать? Давайте искать компромисс.
Обозначим через е(альфа, бета) насколько именно мы не добились равенства:
И мы постараемся минимизировать эту ошибку:
Почему квадратный? Мы ищем не просто минимум нормы, а минимум квадрата нормы.
Почему? Сама точка минимума совпадает, и квадрат дает гладкую функцию (квадратическую функцию аргументов (альфа, бета)), а просто длина дает конусообразную функцию, недифференцируемую в точке минимума.
Брр.
Квадрат удобнее.
Очевидно, что ошибка минимизируется, если вектор е ортогонально плоскости, натянутой векторами я И дж .
Иллюстрация 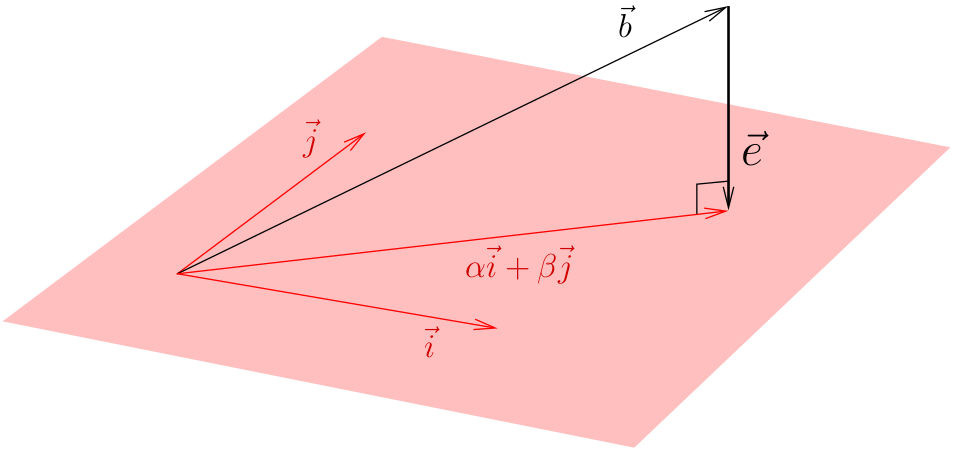
Другими словами: мы ищем такую прямую, чтобы сумма квадратов длин расстояний от всех точек до этой прямой была минимальна: ОБНОВЛЕНИЕ: у меня проблема: расстояние до прямой должно измеряться по вертикали, а не по ортогональной проекции.
Этот Комментатор прав.
Иллюстрация 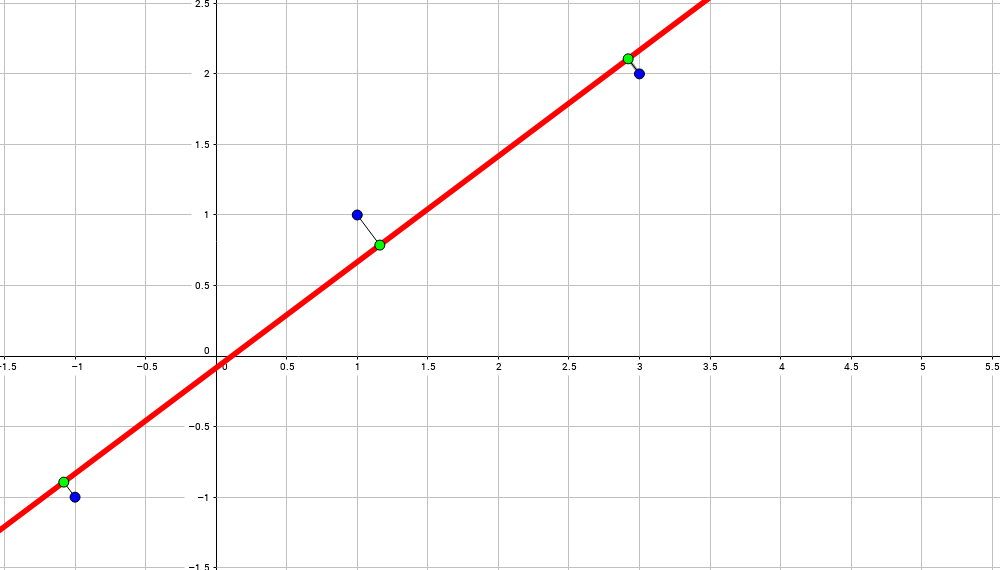
Совсем другими словами (осторожно, плохо формализовано, но должно быть понятно): берем все возможные линии между всеми парами точек и ищем среднюю линию между всеми: Иллюстрация 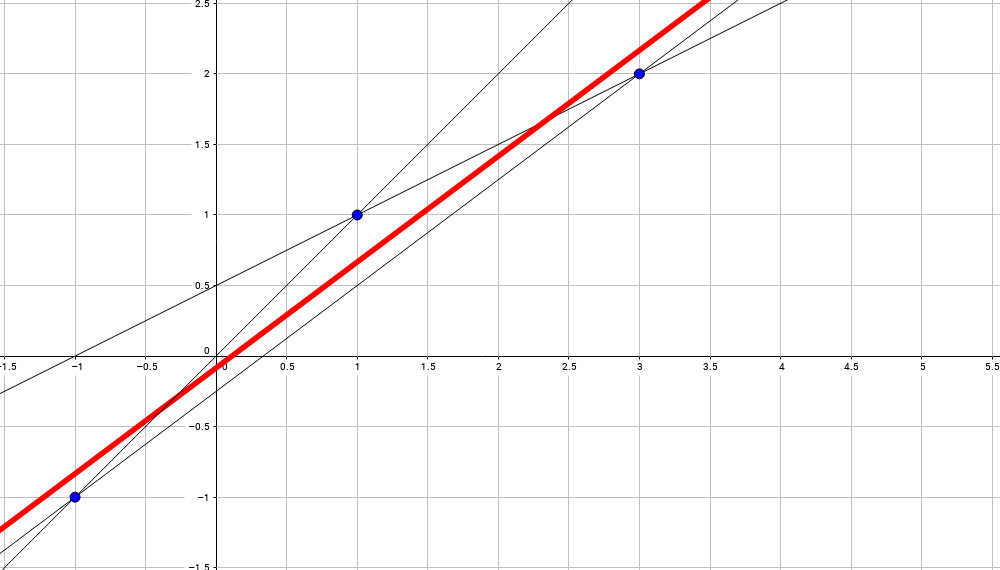
Другое объяснение простое: мы прикрепляем пружину между всеми точками данных (здесь их три) и прямой линией, которую ищем, и прямая линия состояния равновесия — это именно то, что мы ищем.
Минимальная квадратичная форма
Итак, учитывая этот вектор б и плоскость, натянутая на векторы-столбцы матрицы А (в данном случае (x0,x1,x2) и (1,1,1)), ищем вектор е с минимальным квадратом длины.
Очевидно, минимум достижим только для вектора е , ортогональный плоскости, натянутой векторами-столбцами матрицы А :
Другими словами, мы ищем вектор x=(альфа, бета) такой, что:
Напомню, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:
Здесь было бы полезно вспомнить, что матрицу можно интерпретировать и как квадратичную форму, например, единичную матрицу ((1,0),(0,1)) можно интерпретировать как функцию x^2 + y^ 2:
квадратичная форма 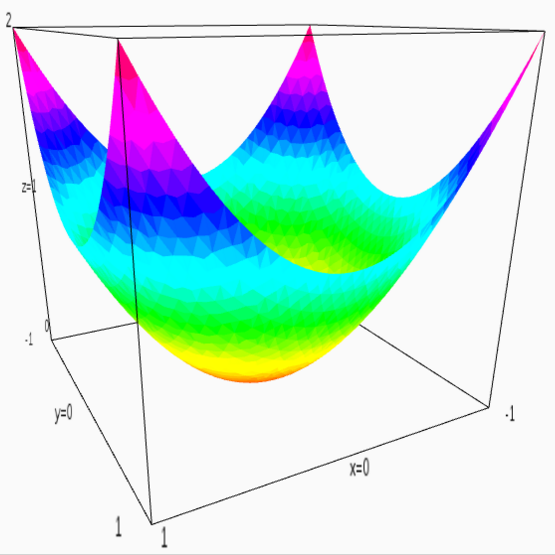
Вся эта гимнастика известна под названием линейная регрессия .
Уравнение Лапласа с граничным условием Дирихле Теперь самая простая реальная задача: есть некая триангулированная поверхность, надо ее сгладить.
Например, давайте загрузим модель моего лица: 
Исходный коммит доступен Здесь .
Чтобы минимизировать внешние зависимости, я взял код своего программного рендерера, уже подробно описано на хабе.
Для решения линейной системы я использую ОпенНЛ , это отличный решатель, который, однако, очень сложен в установке: нужно скопировать два файла (.
h+.
c) в папку с вашим проектом.
Все сглаживание выполняется с помощью следующего кода:
Координаты X, Y и Z разделимы, я сглаживаю их отдельно.for (int d=0; d<3; d++) { nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, verts.size()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<(int)verts.size(); i++) { nlBegin(NL_ROW); nlCoefficient(i, 1); nlRightHandSide(verts[i][d]); nlEnd(NL_ROW); } for (unsigned int i=0; i<faces.size(); i++) { std::vector<int> &face = faces[i]; for (int j=0; j<3; j++) { nlBegin(NL_ROW); nlCoefficient(face[ j ], 1); nlCoefficient(face[(j+1)%3], -1); nlEnd(NL_ROW); } } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<(int)verts.size(); i++) { verts[i][d] = nlGetVariable(i); } }
То есть я решаю три системы линейных уравнений, каждая с количеством переменных, равным количеству вершин в моей модели.
Первые n строк матрицы A содержат только одну единицу в каждой строке, а первые n строк вектора b имеют исходные координаты модели.
То есть я привязываю пружину между новым положением вершины и старым положением вершины — новые не должны отходить слишком далеко от старых.
Все последующие строки матрицы A (faces.size()*3 = количество ребер всех треугольников в сетке) имеют одно вхождение 1 и одно вхождение -1, при этом вектор b имеет нулевые противоположные компоненты.
Это означает, что я поместил пружину на каждый край нашей треугольной сетки: все края пытаются получить ту же самую вершину, что и их начальная и конечная точки.
Еще раз: все вершины являются переменными, и они не могут далеко уйти от исходного положения, но при этом стараются стать похожими друг на друга.
Вот результат: 
Все бы ничего, модель действительно сглажена, но отошла от первоначального края.
Немного изменим код: for (int i=0; i<(int)verts.size(); i++) {
float scale = border[i] ? 1000 : 1;
nlBegin(NL_ROW);
nlCoefficient(i, scale);
nlRightHandSide(scale*verts[i][d]);
nlEnd(NL_ROW);
}
В нашей матрице A для вершин, находящихся на ребре, я добавляю не строку из категории v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d].
Что это меняет? И это меняет нашу квадратичную форму ошибки.
Теперь единичное отклонение от вершины у края будет стоить не одну единицу, как раньше, а 1000*1000 единиц.
То есть на крайние вершины мы повесили более мощную пружину, решение предпочтет сильнее растянуть остальные.
Вот результат: 
Давайте удвоим силу пружины между вершинами: nlCoefficient(face[ j ], 2);
nlCoefficient(face[(j+1)%3], -2);
Логично, что поверхность стала более гладкой: 
А теперь еще во сто крат сильнее: 
Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду.
В результате полученная мыльная пленка будет стараться иметь как можно меньше кривизны, касаясь границы – нашего проволочного кольца.
Это именно то, что мы получили, исправив бордюр и попросив гладкую поверхность внутри.
Поздравляем, мы только что решили Уравнение Лапласа с граничными условиями Дирихле.
Звучит круто? Но на самом деле вам нужно решить всего лишь одну систему линейных уравнений.
Уравнение Пуассона Давай сделаем что-нибудь круче Давайте вспомним имя.
Допустим, у меня есть такое изображение: 
Всем нравится, но мне стул не нравится.
Я разрезаю картинку пополам: 

А стул я выберу руками: 
Затем я перетяну все, что белое в маске, в левую часть картинки, и при этом по всей картинке буду говорить, что разница между двумя соседними пикселями должна быть равна разнице между двумя соседними пикселями справа.
картина: for (int i=0; i<w*h; i++) {
if (m.get(i%w, i/w)[0]<128) continue;
nlBegin(NL_ROW);
nlCoefficient(i, 1);
nlRightHandSide(a.get(i%w, i/w)[0]);
nlScaleRow(100);
nlEnd(NL_ROW);
}
for (int i=0; i<w-1; i++) {
for (int j=0; j<h-1; j++) {
for (int d=0; d<2; d++) {
nlBegin(NL_ROW);
int v1 = b.get(i, j )[0];
int v2 = b.get(i+d, j+1-d)[0];
nlCoefficient( i + j *w, 1);
nlCoefficient((i+d)+(j+1-d)*w, -1);
nlRightHandSide(v1-v2);
nlScaleRow(10);
nlEnd(NL_ROW);
}
}
}
Вот результат: 
Код и изображения доступны.
Пример из жизни Я сознательно не стал делать вылизанные результаты, потому что.
Я просто хотел показать, как именно можно применять методы наименьших квадратов, это обучающий код. Теперь приведу пример из жизни:
У меня есть несколько фотографий таких образцов ткани: 
Моя задача — сделать бесшовные текстуры из фотографий такого качества.
Для начала я (автоматически) ищу повторяющийся узор: 
Если я вырежу этот четырехугольник прямо, то из-за искажения края не сойдутся, вот пример узора, повторенного четыре раза: Скрытый текст 
Вот фрагмент, где хорошо виден шов: 
Поэтому я не буду резать по прямой, вот линия разреза: Скрытый текст 
А вот шаблон, повторенный четыре раза: Скрытый текст 
И фрагмент, чтобы было понятнее: 
Уже лучше, срез прошел не по прямой, избегая всяких завитков, но шов все равно виден из-за неравномерного освещения на исходной фотографии.
Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона.
Вот конечный результат после выравнивания освещения: 
Текстура получилась идеально бесшовной, и все это автоматически с фотографии весьма посредственного качества.
Не бойтесь математики, ищите простые объяснения, и будет вам счастье в технике.
Теги: #математика на пальцах #геометрия для пятого класса #геометрия для пятого класса #наименьшие квадраты #уравнение Лапласа #уравнение Пуассона #математика для программистов #программирование #C++ #Алгоритмы #математика

-
Порошковая Металлургия
19 Oct, 24 -
Вредоносное Программное Обеспечение
19 Oct, 24 -
Эмулятор Ритм-Студии Jdrum
19 Oct, 24 -
Структурные Сборки В Nanocad Design Bim
19 Oct, 24


