Массивы, Коллекции: алгоритмический минимум
Массивы и списки
Недавно во время собеседования в крупной компании на должность Java-разработчика меня попросили реализовать стандартный алгоритм сортировки.Поскольку я никогда не реализовал самодельные алгоритмы сортировки, а всегда использовал готовые решения, у меня возникли трудности с реализацией.
После интервью я решил разобраться в вопросе и подготовить список основных алгоритмов сортировки и поиска, которые используются в стандартном java-пакете — Java Collections Framework (JCF).
Для этого я изучил источники Oracle JDK 7.80 ( УПД : ссылка добавлена).
В самом общем виде результат исследования представлен на рисунке.
Подробности в основном тексте.
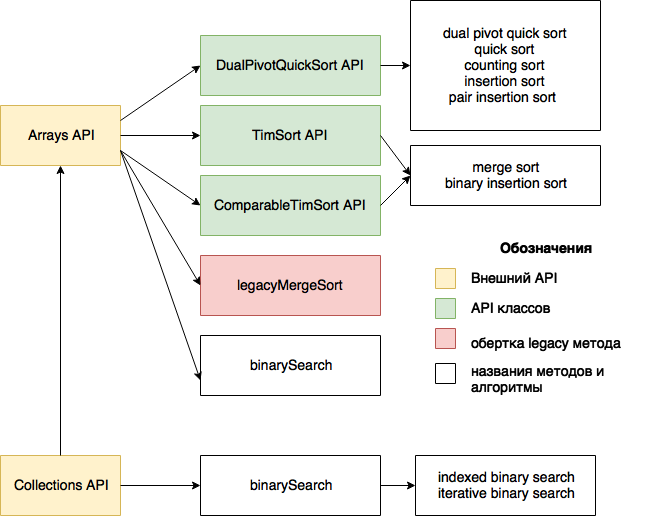
Рисунок 1. Методы Массивы, Коллекции и алгоритмы, которые они реализуют.
Первое, что меня поразило в алгоритмах, реализованных в Arrays and Collections, это то, что их можно буквально пересчитать по пальцам — по сути, это два алгоритма сортировки и один алгоритм поиска.
Во-вторых, сортировка списка использует сортировку массива.
В-третьих, один из алгоритмов сортировки портирован с Python. Алгоритм быстрой сортировки с двумя эталонными элементами был разработан нашим соотечественником Владимиром Ярославским и реализован при участии Джона Бентли и Джошуа Блоха.
Алгоритм сортировки слиянием, являющийся основным алгоритмом сортировки массивов ссылочных типов, назван буквально в честь своего создателя Тима Питерса — TimSort. Этот алгоритм был адаптирован Джошуа Блохом на основе алгоритма сортировки списков, реализованного на Python Тимом Питерсом.
Кратко подводя итоги, стоит отметить, что:
- Можно условно выделить три слоя методов:
- Методы API
- Методы базовых (основных) алгоритмов
- Методы (блоки) дополнительных алгоритмов
- Используются три основных алгоритма.
Два алгоритма сортировки: быстрая сортировка, сортировка слиянием.
Один алгоритм поиска: бинарный поиск.
- Для оптимизации «основные» алгоритмы заменяются на «дополнительные», более подходящие на данный момент (полный список алгоритмов и условий переключения приведен в конце)
- Для определения того, какой из «дополнительных» алгоритмов будет использоваться, можно использовать:
- сигнатуры методов (типы аргументов, логические переменные)
- Флаги виртуальной машины
- Пороги длины массива/списка, хранящиеся в переменных частного класса
В качестве основного сервиса они предоставляют методы сортировки и поиска.
Для совместимости API коллекций и API массивов унифицированы.
Пользователю предоставляется сортировка статических перегрузок и бинарный поиск.
Разница в том, что методы API Arrays принимают массивы примитивных и ссылочных типов, а методы API sort иbinarySearch Collections принимают только списки.
Итак, чтобы узнать, какие основные и дополнительные алгоритмы используются в пакете util, нужно проанализировать реализацию 4-х методов из Collections API и Arrays API. Таблица 1. Массивы API и коллекции API
| Метод | API массивов | API коллекций |
|---|---|---|
| Метод сортировки | Массивы.
сортировать |
Коллекции.
сортировать |
| Метод поиска | Массивы.
binarySearch |
Коллекции.
binarySearch |
Массивы.
сортировать Массивы примитивных типов Базовый алгоритм сортировки массивов примитивных типов в Arrays: быстрая сортировка .
Для реализации этой сортировки предоставляется последний класс DualPivotQuickSort, который предоставляет общедоступные методы сортировки для сортировки массивов всех примитивных типов данных.
Методы API массивов вызывают эти методы и передают в них ссылку на массив.
Если вам нужно отсортировать определенный диапазон массива, то также передаются индексы начала и конца диапазона.
Временная сложность алгоритма быстрой сортировки составляет O(n log n) в лучшем и среднем случае.
В некоторых случаях (например, на небольших массивах) алгоритм быстрой сортировки не обладает лучшей производительностью и деградирует до квадратичной сложности.
Поэтому имеет смысл использовать вместо него другие алгоритмы, которые в целом проигрывают, но в конкретных случаях могут дать выигрыш.
В качестве дополнительных алгоритмов были выбраны: сортировка вставками, «обычная» быстрая сортировка (с одной контрольной точкой), сортировка по подсчету .
Инженеры Oracle эмпирически рассчитали оптимальные размеры массивов для каждого дополнительного алгоритма сортировки.
Эти значения записываются в приватные поля класса DualPivotQuickSort. Для наглядности я свел их в таблицу 2. Таблица 2. Дополнительные алгоритмы в DualPivotQuickSort.sort
| Типы данных | Размер массива, n | Предпочтительный алгоритм | Временная сложность в лучшем случае |
|---|---|---|---|
| int, long, short, char, float, double | н < 47 | сортировка вставкой сортировка парной вставкой | На) |
| int, long, short, char, float, double | н < 286 | быстрая сортировка | О (п журнал п) |
| байт | 29 < n | сортировка по подсчету | О(п+к) |
| короче, персонаж | 3200 < n | сортировка по подсчету | О(п+к) |
Массивы примитивных типов.
Выбор алгоритма и крайний левый логический параметр Самый левый параметр дополнительно передается методу сортировки и указывает, является ли указанная часть самой левой в диапазоне.
Если да, то применяется «обычный» алгоритм сортировки вставками.
Если нет, то применяется попарная сортировка вставками.
Вы можете прочитать еще одно объяснение о выборе дополнительных алгоритмов.
Здесь .
Массивы ссылочных типов Для массивов ссылочных типов алгоритм сортировки слиянием предусмотрен как основной; реализован в трёх вариантах.
Две текущие реализации помещены в специальные классы: TimSort, ComparableTimSort. TimSort предназначен для сортировки объектов с помощью компараторов.
ComparableTimSort — это версия TimSort, предназначенная для сортировки объектов, поддерживающих Comparable. Подробности о реализации сортировки TimSort см.
Класс TimSort содержит единственное пороговое значение, при сравнении с которым принимается решение о переходе на дополнительный алгоритм.
Это значение называется MIN_MERGE и хранит минимальную длину массива, при которой будет выполняться сортировка слиянием.
Если длина массива меньше MIN_MERGE, то есть 32, то будет использоваться двоичная сортировка вставкой.
Как сказано в документации, это мини-TimSort, т.е.
без использования слияний.
Таблица 3. Дополнительные алгоритмы в TimSort.sort и ComparableTimSort.sort
| Тип данных | Размер массива, n | Предпочтительный алгоритм | Временная сложность в лучшем случае |
|---|---|---|---|
| Т[] | н < 32 | двоичная сортировка вставкой | На) |
Устаревшая сортировка заключена в методе HeritageMergeSort и непосредственно реализована в методе Arrays.mergeSort. Чтобы использовать его, перед запуском виртуальной машины необходимо установить флаг -Djava.util.Arrays.useLegacyMergeSort=true. Для хранения значения этой переменной в Arrays имеется внутренний статический класс LegacyMergeSort (см.
листинг 1).
Листинг 1. Статический внутренний класс LegacyMergeSort в Arrays
При вызове Arrays.sort с массивом ссылочного типа выполняется проверка, установлен ли флаг на использование устаревшей сортировки.static final class LegacyMergeSort { private static final boolean userRequested = java.security.AccessController.doPrivileged( new sun.security.action.GetBooleanAction( "java.util.Arrays.useLegacyMergeSort")).booleanValue(); }
Затем выполняется вызов либо устаревшей сортировки, либо одной из базовых (см.
листинг 2).
Листинг 2. Реализация метода Arrays.sort для массива ссылочного типа с компаратором public static <T> void sort(T[] a, Comparator<? super T> c) {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, c);
else
TimSort.sort(a, c);
}
Массивы.
binarySearch Бинарный поиск предусмотрен для массивов как примитивного, так и ссылочного типов.
Перед поиском массив необходимо отсортировать.
Сложность алгоритма бинарного поиска в среднем и в худшем случае составляет O(log n).
Никаких дополнительных алгоритмов не предусмотрено.
Коллекции.
сортировать Коллекции обеспечивают сортировку только для списков.
Интересно, что сначала список преобразуется в массив, а затем сортируется слиянием массивов ссылочных типов.
Сортировка выполняется вызовом метода Arrays.sort.
Коллекции.
binarySearch Как и в случае с сортировкой, Collections реализует двоичный поиск только для списков.
Переменная BINARYSEARCH_THRESHOLD устанавливает ограничение размера списка на 5000 элементов.
Поэтому, если вам нужно выполнить поиск по большей выборке, вам придется подумать, как лучше всего это сделать.
Списки поддерживают либо произвольный доступ, либо последовательный .
Если список поддерживает произвольный доступ, то он будет обработан алгоритмом индексированный бинарный поиск .
Если список поддерживает последовательный доступ, то он будет обработан по алгоритму итеративный двоичный поиск .
Как видите, в обоих случаях будет использоваться двоичный поиск.
Всего интерфейс List в JDK 7.8 реализован 10 классами, 2 из которых — абстрактные AbstractList и AbstractSequentialList. Последовательный доступ реализуется только LinkedList и всеми потомками AbstractSequentialList. Поэтому они будут обработаны алгоритмом iteratorBinarySearch. Остальные списки, такие как ArrayList, CopyOnWriteArrayList, будут обрабатываться алгоритмом indexedBinarySearch. УПД.
Как выяснилось из личной беседы с Замыслов , необходимо уточнить, как BINARYSEARCH_THRESHOLD участвует в определении типа алгоритма сортировки.
Этот порог влияет только на последовательные списки.
Список, поддерживающий произвольный доступ, всегда будет обрабатываться Collections.indexedBinarySearch. А список, поддерживающий последовательный доступ, будет обрабатываться Collections.iteratorBinarySearch только в том случае, если он превышает значение BINARYSEARCH_THRESHOLD (см.
листинг 3), в противном случае он также будет обрабатываться Collections.indexedBinarySearch.
Листинг 3. Влияние типов списков и константы BINARYSEARCH_THRESHOLD на определение алгоритмов обработки списков int binarySearch(List<? extends Comparable<? super T>> list, T key) {
if (list instanceof RandomAccess || list.size()<BINARYSEARCH_THRESHOLD)
return Collections.indexedBinarySearch(list, key);
else
return Collections.iteratorBinarySearch(list, key);
}
Подведем итог тому, что мы узнали
Теперь, когда основные методы и условия перехода к дополнительным методам рассмотрены, можно обобщить полученные данные.Для максимальной наглядности детализируем рисунок 1, выделив основные методы и добавив условия перехода к дополнительным методам.
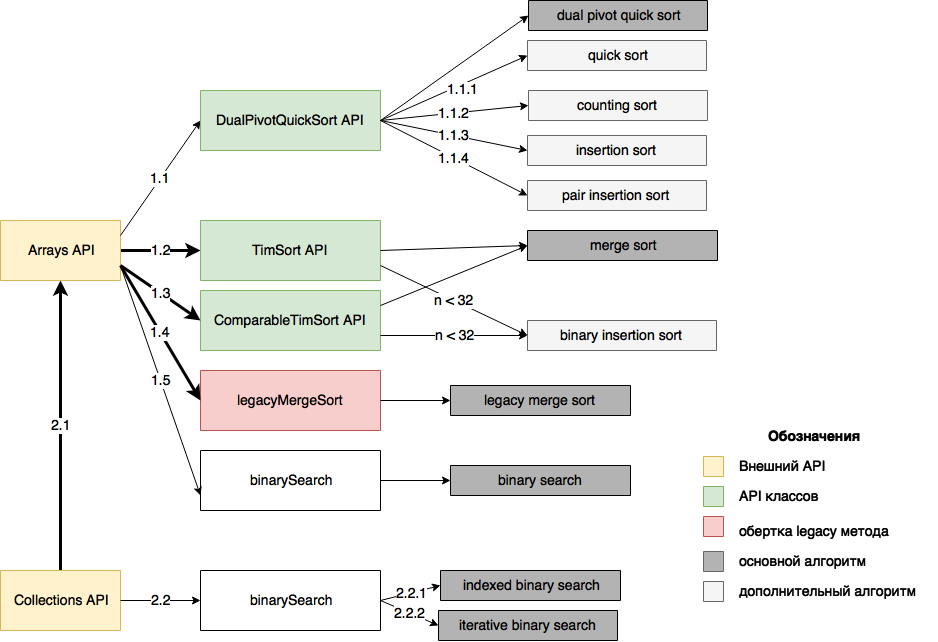
Рисунок 2. Основные и дополнительные алгоритмы Массивы, Коллекции
Пояснения к цифрам на стрелках на рисунке 2 содержатся в сводной таблице.
Цифры обозначают условия перехода.
Основные алгоритмы выделены серым цветом.
Они применяются по умолчанию.
В сводной таблице темно-серым цветом выделены строки, описывающие основные алгоритмы.
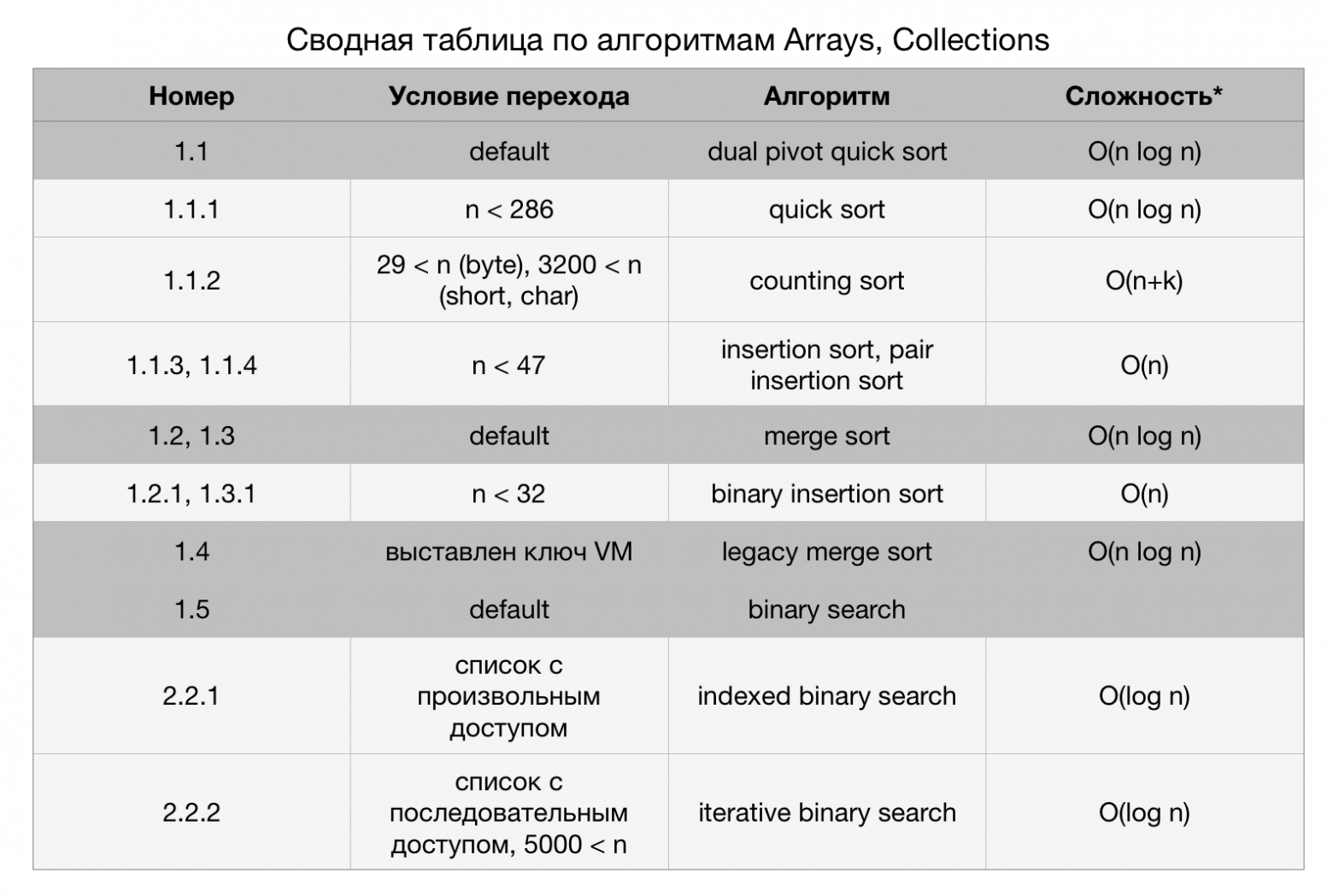
*Сложности основных алгоритмов указаны как «средний случай», а трудности дополнительных алгоритмов – как «лучший случай».
Заключение
Целью заметки было составление полного списка алгоритмов, используемых для поиска и сортировки массивов и списков в пакете java.util. Итак, чтобы полностью понять, что происходит «под капотом» при использовании Arrays API и Collections API, достаточно освоить следующие алгоритмы:- быстрая сортировка с двумя контрольными точками
- быстрая сортировка с одной контрольной точкой
- сортировка по подсчету
- «простая» сортировка вставкой
- двоичная сортировка вставкой
- сортировка попарными вставками
- сортировка слиянием (версия Тима Питерса)
- двоичный поиск
- индексированный бинарный поиск
- итеративный двоичный поиск
- О сортировке списков
- Алгоритмы обработки массивов в Arrays
- Знать сложности алгоритмов
- Алгоритм сортировки Timsort
- Статья Ярославского об алгоритме быстрой сортировки Спасибо за ссылку Макчимо
- Алгоритмы сортировки в виде пошаговой анимации
- Последовательный и произвольный доступ

-
Японские И Калифорнийские Модели Кано
19 Oct, 24 -
Почему В Матрице Смоделирован 1999 Год?
19 Oct, 24 -
Управление Голосом Или Правильным Сообщением
19 Oct, 24 -
Личная Проблема В Личном Блоге
19 Oct, 24


