Заранее отмечу, что тот, кто знает, как учится перцептрон, вряд ли найдет в этой статье что-то новое.
Вы можете смело пропустить это.
Почему я решил это написать — мне бы хотелось написать серию статей, связанных с нейронными сетями и использованием TensorFlow.js, поэтому я не мог опустить общетеоретические выдержки.
Поэтому прошу отнестись к финальной идее с большим терпением и пониманием.
В классическом программировании разработчик описывает на конкретном языке программирования некий жестко определенный набор правил, который был определен на основе его знаний в конкретной предметной области и который в первом приближении описывает процессы, происходящие в мозгу человека.
при решении аналогичной задачи.
Например, можно запрограммировать стратегию игры в крестики-нолики, шахматы и многое другое (рис.
1).

Рисунок 1 – Классический подход к решению проблем
В то время как алгоритмы машинного обучения могут определять набор правил решения задач без участия разработчика, а только на основе наличия набора обучающих данных.
Обучающий набор — это некоторый набор входных данных, связанный с набором ожидаемых результатов (ответов, выходных данных).
На каждом этапе обучения модель, изменяя свое внутреннее состояние, будет оптимизировать и уменьшать ошибку между фактическим выходным результатом модели и ожидаемым результатом (рис.
2).

Рисунок 2 – Машинное обучение
Нейронные сети
Долгое время учёные, вдохновленные процессами, происходящими в нашем мозгу, пытались реконструировать центральную нервную систему и попытаться имитировать работу человеческого мозга.Благодаря этому родилось целое направление в машинном обучении — нейронные сети.
На рисунке 3 вы можете увидеть сходство между конструкцией биологического нейрона и математическим представлением нейрона, используемым в машинном обучении.

Рисунок 3 – Математическое представление нейрона
В биологическом нейроне нейрон получает электрические сигналы от дендритов, которые модулируют электрические сигналы различной силы, которые могут возбудить нейрон при достижении определенного порогового значения, что, в свою очередь, приведет к передаче электрического сигнала другим нейронам через синапсы.
.
Персептрон
Математическая модель нейронной сети, состоящей из одного нейрона, выполняющего две последовательные операции (рис.
4): вычисляет сумму входных сигналов с учетом их весов связи (проводимость или сопротивление)
применяет функцию активации к общему эффекту входных сигналов.
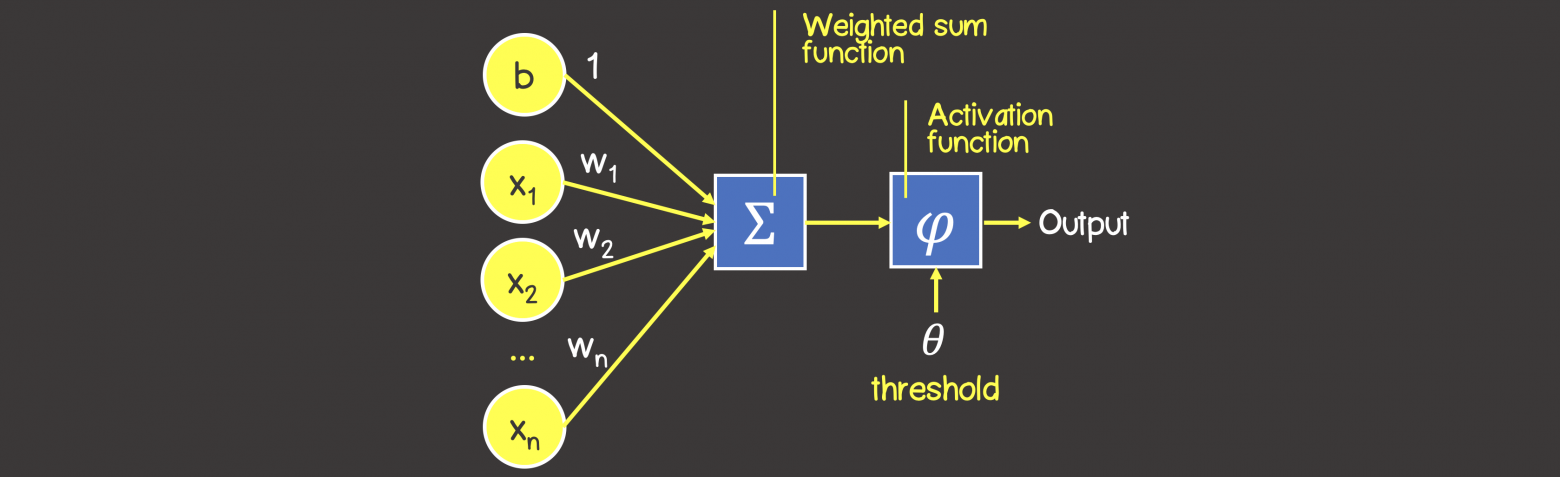
Рисунок 4 – Математическая модель перцептрона
В качестве функции активации можно использовать любую дифференцируемую функцию; наиболее часто используемые из них приведены в таблице 1. Выбор функции активации ложится на плечи инженера, и обычно этот выбор основывается либо на имеющемся опыте решения подобных задач, либо просто на методе выбора.
Таблица 1 – Общие функции активации Имя Формула Расписание Линейная функцияЗаметка
Однако есть рекомендация — если в нейронной сети нужна нелинейность, то в качестве функции активации лучше всего подойдет функция ReLU, имеющая лучшие показатели сходимости модели в процессе обучения.

.
Сигмовидная функция
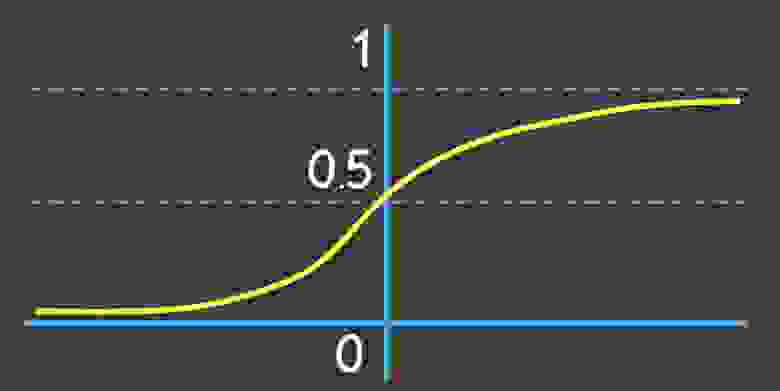
Функция Софтмакс
Используется для задач классификации (где количество классов больше 2).
Функция гиперболического тангенса

Сжимает входной сигнал в диапазоне [-1, 1].
Используется в скрытых слоях нейронной сети, так как центрирует выходной сигнал относительно нуля, что ускоряет процесс обучения.
Выпрямленный линейный блок (ReLU)
Используется в скрытых слоях нейронной сети, имеет лучшую сходимость, чем сигмовидная и танх-функции.
Дырявый РеЛУ
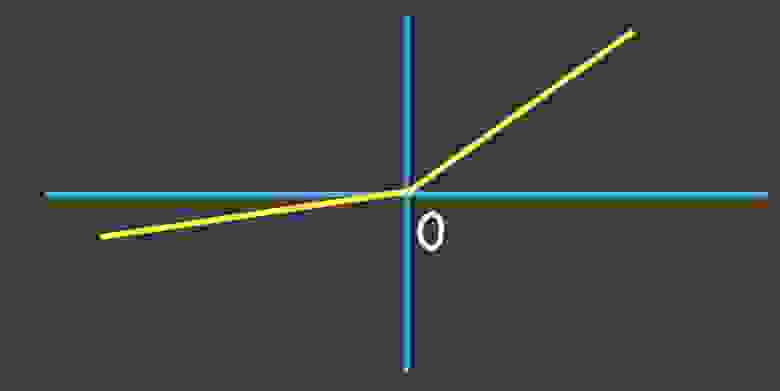
Устранен недостаток функции ReLU в интервале отрицательных выходных сигналов, где частная производная равна 0.
Процесс обучения перцептрона
Процесс обучения состоит из нескольких этапов.Для большей наглядности рассмотрим некую вымышленную задачу, которую мы будем решать с помощью нейронной сети, состоящей из одного нейрона с линейной функцией активации (это по сути персептрон вообще без функции активации).
Также для упрощения задачи исключим в нейроне узел смещения b (рис.
5).

Рисунок 5 – Набор обучающих данных и состояние нейронной сети на предыдущем этапе обучения
На этом этапе мы имеем нейронную сеть в определенном состоянии с определенными весами связей, которые были рассчитаны на предыдущем этапе обучения модели, либо, если это первая итерация обучения, то веса связей выбираются в случайном порядке.
Итак, представьте, что у нас есть некий набор обучающих данных, значения каждого элемента из набора представлены вектором входных данных, содержащим 2 параметра (признака)
.
Под
в модели, в зависимости от рассматриваемой предметной области, может подразумеваться что угодно: количество комнат в доме, удаленность дома от моря, или мы просто пытаемся научить нейросеть логической операции И или ИЛИ .
Каждый вектор входных данных в обучающем наборе связан с вектором ожидаемого результата.
В этом случае вектор выходных данных содержит только один параметр, который, опять же, в зависимости от выбранной предметной области, может означать что угодно – цену дома, результат логической операции И или ИЛИ.
ШАГ 1 – Процесс прямой связи На этом этапе мы вычисляем сумму входных сигналов с учетом веса каждого соединения и применяем функцию активации (в нашем случае функция активации отсутствует).
Проведем расчеты для первого элемента обучающего набора:

Рисунок 6 – Прямое распространение ошибки
Обратите внимание, что написанная выше формула представляет собой упрощенное математическое уравнение для частного случая операций над тензорами.
Тензор По сути, это контейнер данных, который может иметь N осей и произвольное количество элементов вдоль каждой из осей.
Большинству людей знакомы тензоры из математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строками, столбцами).
Формулу можно записать в следующем виде, где вы увидите знакомые матрицы (тензоры) и их умножение, а также поймете, о каком упрощении шла речь выше:
ШАГ 2 – Вычислите функцию ошибки Функция ошибок — это метрика, отражающая несоответствие между ожидаемыми и полученными результатами.
Обычно используются следующие функции ошибок:
— Среднеквадратическая ошибка (MSE) – эта функция ошибок особенно чувствительна к выбросам в обучающем наборе, поскольку она использует квадрат разницы между фактическим и ожидаемым значениями (выброс – это значение, которое очень далеко от других значений в наборе данных, которые иногда могут возникать из-за ошибок в данных, таких как смешивание данных с разными единицами измерения или неверные показания датчиков):
— среднеквадратичное отклонение (Root MSE) - по сути, это то же самое, что среднеквадратическая ошибка в контексте нейронных сетей, но может отражать реальную физическую единицу измерения, например, если в нейронной сети выходными параметрами нейронной сети является цена дом, выраженный в долларах, то единицей измерения среднеквадратической ошибки будет доллар в квадрате (
), а для стандартного отклонения это доллар ($), что, естественно, немного упрощает задачу человеческого анализа:
— среднее отклонение (средняя абсолютная ошибка, MAE) - в отличие от двух вышеуказанных значений, он не столь чувствителен к выбросам:
— Перекрестная энтропия – использует для задач классификации:
Где
– количество экземпляров в обучающем наборе
– количество классов при решении задач классификации
— ожидаемое выходное значение
– фактическое выходное значение обученной модели
Для нашего конкретного случая мы будем использовать MSE:
ШАГ 3 – Обратное распространение ошибки Цель обучения нейронной сети проста: минимизация функции ошибок:
Один из способов найти минимум функции — модифицировать веса связей на каждом последовательном шаге обучения в направлении, противоположном вектору градиента — метод градиентного спуска, и математически это выглядит так:
Где
– k-я итерация обучения нейронной сети;
– скорость обучения и задается инженером, обычно она может составлять 0,1; 0,01 (подробнее о том, как этап обучения влияет на процесс конвергенции обучения, чуть позже)
– градиент функции ошибки
Чтобы найти градиент, мы используем частные производные по отношению к пользовательским аргументам.
:
В нашем конкретном случае с учетом всех упрощений функция ошибок принимает вид:
Памятка производных формул
Напомним некоторые производные формулы, полезные для вычисления частных производных.Найдем следующие частные производные:
Тогда процесс обратного распространения ошибки представляет собой движение по модели от выхода ко входу с изменением весов модели в направлении, противоположном вектору градиента.
Установив шаг обучения на 0,1 (скорость обучения), мы имеем (рис.
7):

Рисунок 7 – Обратное распространение ошибки
Таким образом, мы завершили этап обучения k+1, чтобы убедиться, что ошибка уменьшилась и выходные данные модели с новыми весами стали ближе к ожидаемым.
Выполним процесс прямого распространения ошибки по модели с новыми весами (см.
ШАГ 1):
Как мы видим, выходное значение увеличилось на 0,2 единицы в нужную сторону в сторону ожидаемого результата – единицы (1).
Тогда ошибка будет:
Как видите, на предыдущем шаге обучения ошибка была 0,64, а с новыми весами — 0,36, поэтому мы настроили модель в правильном направлении.
Следующая часть статьи: Машинное обучение.
Нейронные сети (часть 2): ИЛИ-моделирование; XOR с TensorFlow.js Машинное обучение.
Нейронные сети (часть 3) — Сверточная сеть под микроскопом.
Изучение API Tensorflow.js Теги: #Машинное обучение #нейронные сети #персептрон

-
Продажи Электромобилей В Канаде
19 Oct, 24 -
Селен Для Python. Глава 2. Первые Шаги
19 Oct, 24


