Постановка задачи Рассмотрим задачу аппроксимации комбинации прямых из набора зашумленных координат точек, расположенных на заданной комбинации прямых (см.
рис.
1 и рис.
2).
Обычная формула линейной аппроксимации здесь не подойдет, так как точки перемешиваются и результатом будет некая усредненная линия между ними (см.
рис.
3).
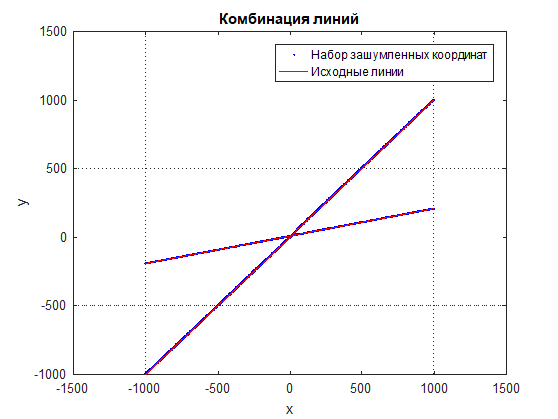
Рис.
1 Комбинация линий и зашумленного набора координат 
Рис.
2 Сочетание линий и зашумленного набора координат в увеличенном масштабе 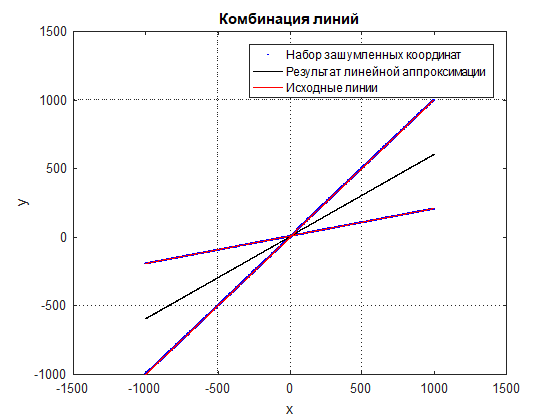
Рис.
3 Результат линейной аппроксимации
Алгоритм
Единственный выход, который пришел в голову, это попробовать разные варианты лесок.Те.
проходим все возможные углы, естественно по ограниченной сетке, от -90 градусов до +90 градусов (от -180 до 180 бессмысленно, т.к.
линия симметрична относительно центра координат).
Таким образом, перебрав все возможные варианты углов, мы оцениваем угол наклона линии, при котором наибольшее количество точек находится на одинаковом расстоянии.
Этот угол является искомым углом наклона линии, но он приблизителен из-за дискретности исходного набора углов.
Далее по полученному набору точек строим линейную аппроксимацию и получаем наиболее приближенную аппроксимацию первой линии.
Для нахождения следующей линии точки, использованные на предыдущем этапе, удаляются из рассмотрения.
Таким образом, построчно аппроксимируем все линии.
1. Рассматриваемый набор углов
На этом этапе необходимо выяснить, какой набор углов будет перемещен.Зная особенности конкретной задачи, можно скорректировать этот набор углов, тем самым ускорив процесс обнаружения линий.
Также можно учитывать особенности угла наклона между линиями, то есть на каждом следующем шаге сужать диапазон сортируемых углов.
В этой задаче мы будем использовать равномерный набор углов от -90 до 90 градусов во лбу с шагом 0,1 градуса.
2. Определение расстояния от точки до линии
Для удобства перебора всех возможных вариантов линий нам необходимо вывести формулу оценки кратчайшего расстояния от точки до линии.
Пусть уравнение линии и координаты точки, от которой мы измеряем расстояние, примут следующие обозначения:
Тогда, поскольку кратчайшее расстояние от точки до прямой есть перпендикуляр к этой прямой, получим следующее уравнение для перпендикуляра, проходящего через данную точку:
Затем точка пересечения этих двух линий:
Получаем расстояние от интересующей точки до точки пересечения:
3. Построение гистограммы расстояний
Если мы просто построим гистограмму расстояний, то она будет неинформативна, поэтому нам нужно строить гистограмму с помощью скользящего окна, так она будет более плавной и мы получим результат с меньшей ошибкой (см.Рис.
4-6).
По построенной гистограмме определяем расстояние с максимальным количеством точек.
На основе полученного набора максимального количества точек для каждого угла построим зависимость количества точек и угла наклона линии (см.
рис.
7, 8).
На рис.
7 можно увидеть два четких пика, эти пики представляют собой углы наклона интересующих нас линий.

Рис.
4 Гистограмма расстояний (ошибочная линия) 
Рис.
5 Гистограмма расстояний (правильная линия) 
Рис.
6 Увеличенная гистограмма расстояний (правильная линия)
Рис.
7 Гистограмма распределения максимального количества эквидистантных точек в зависимости от угла наклона рассматриваемой линии (Шаг 1) 
Рис.
8 Гистограмма распределения максимального количества равноудаленных точек в зависимости от угла наклона рассматриваемой линии (Шаг 2)
4. Построение линейной аппроксимации.
Угол линии, полученный по гистограмме, является неточным, поскольку он был получен на фиксированной сетке углов.
Для получения более точного угла наклона и смещения интересующей линии необходимо выполнить линейную аппроксимацию полученного набора точек по следующим формулам (см.
рис.
9 и рис.
10):

Рис.
9 Результат аппроксимации первой линии 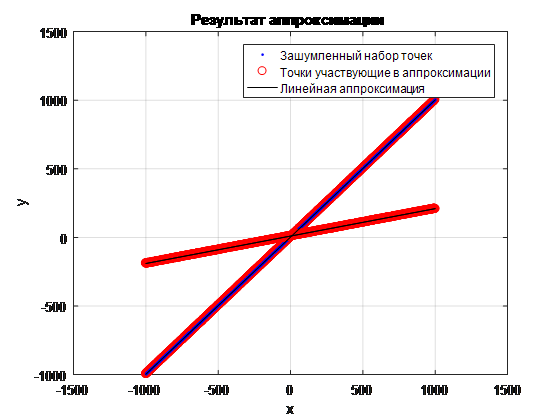
Рис.
10 Результат аппроксимации второй линии
Примеры использования
Приведем примеры распознавания линий на произвольных множествах точек (см.рис.
11-13).

Рис.
11 Результат работы по произвольной выборке точек 
Рис.
12 Результат работы по произвольной выборке точек 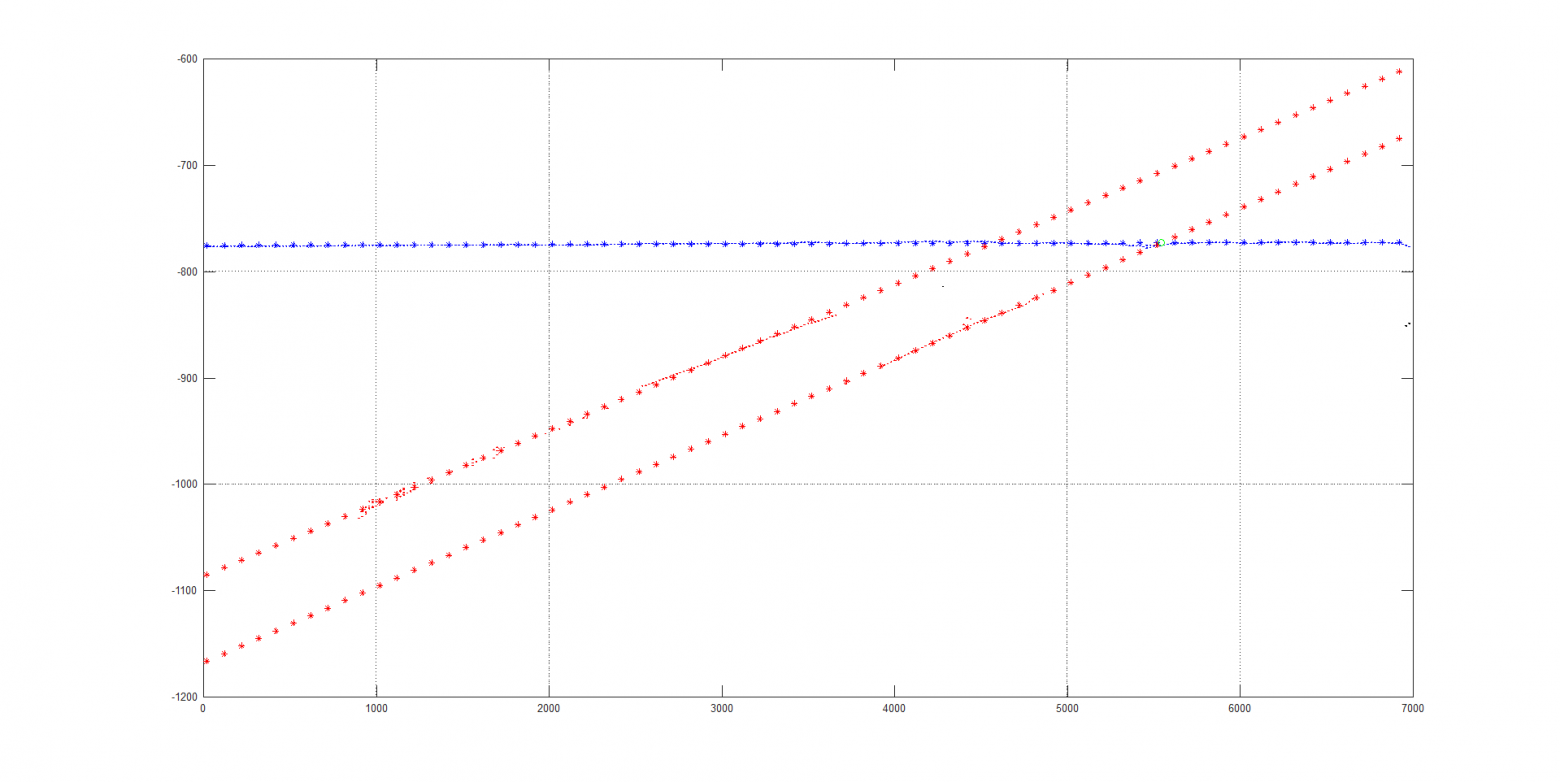
Рис.
13 Результат работы по произвольной выборке точек
Заключение
Используя приведенный выше алгоритм, можно обнаружить прямые линии на относительно высокой скорости и определить их параметры (наклон и смещение).Количество строк может быть неограниченным.
Для успешного обнаружения линии желательно, чтобы точки были разбросаны как можно шире по всей системе координат, так как если все точки находятся рядом, то при процедуре обнаружения с одной линии на другую точки новой линии будут отбрасываться.
из-за их близости к линии предыдущей итерации.
Основная цель этой статьи — посмотреть со стороны, сталкивался ли кто-нибудь с подобными проблемами и как вы их решили.
Внезапно появились методы, которые могут обнаружить эти строки за один проход. Посмотрите несколько интересных решений, которые можно использовать в других задачах.
Теги: #Алгоритмы #Обработка изображений #алгоритмы обработки изображений

-
3 Лучших Недорогих Android-Планшета
19 Oct, 24 -
Хабраман, Где Ты Живешь?
19 Oct, 24 -
Пост-Опрос О Фрилансе
19 Oct, 24


