Массачусетский Институт Технологий.
Курс лекций №6.858. «Безопасность компьютерных систем».
Николай Зельдович, Джеймс Микенс.
2014 год Безопасность компьютерных систем — это курс, посвященный проектированию и внедрению безопасных компьютерных систем.
Лекции охватывают модели угроз, атаки, ставящие под угрозу безопасность, а также методы обеспечения безопасности, основанные на последних научных работах.
Темы включают безопасность операционной системы (ОС), возможности, управление информационными потоками, языковую безопасность, сетевые протоколы, аппаратную безопасность и безопасность веб-приложений.
Лекция 1: «Введение: модели угроз» Часть 1 / Часть 2 / Часть 3 Лекция 2: «Контроль хакерских атак» Часть 1 / Часть 2 / Часть 3 Лекция 3: «Переполнение буфера: эксплойты и защита» Часть 1 / Часть 2 / Часть 3 Лекция 4: «Разделение привилегий» Часть 1 / Часть 2 / Часть 3 Лекция 5: «Откуда берутся ошибки системы безопасности» Часть 1 / Часть 2 Лекция 6: «Возможности» Часть 1 / Часть 2 / Часть 3 Лекция 7: «Нативная клиентская песочница» Часть 1 / Часть 2 / Часть 3 Лекция 8: «Модель сетевой безопасности» Часть 1 / Часть 2 / Часть 3 Лекция 9: «Безопасность веб-приложений» Часть 1 / Часть 2 / Часть 3 Лекция 10: Символическое исполнение Часть 1 / Часть 2 / Часть 3 Аудитория: Кажется, вы еще не говорили о том, как биты используются для хранения целого числа.
Профессор: Это очень хороший вопрос.
И это действительно связано с тем, как вы определяете свои ограничения, верно? Итак, если вы посмотрите на наш простой пример с самого начала, вы увидите, что мы предполагали существование целых чисел, которые мы изучали в начальной школе.
В то же время мы решили полностью игнорировать ошибки переполнения.
Если вас беспокоят ошибки переполнения, и вам важно, чтобы такие ошибки не возникали, то использование целых математических чисел не поможет устранить проблему.
Вам нужно представить эти величины не целыми числами, а битовыми векторами.
Когда вы представляете их в виде битовых векторов, вам приходится смотреть на вещи шире.
Здесь мы возвращаемся к решателям SMT. Аспект модульной теории заключается в том, что сам решатель можно расширять с помощью различных теорий.
Наиболее популярными теориями являются теории битовых векторов фиксированной длины.
Это означает, что если вы интерпретируете свои формулы в теории битовых векторов фиксированной длины, вам необходимо заранее задать длину битовых векторов.
То есть вы должны явно указать, что это будет использоваться для битовых векторов длиной 32 бита, или 8 бит, или 64 бита.

Существует еще одна теория, называемая теорией массивов TOA. И мы еще немного поговорим об этом.
В отличие от теории битовых векторов, которая предназначена для объектов фиксированной длины, теория массивов предназначена для коллекций, размер которых априори неизвестен.
Сейчас на практике никто не использует теорию массивов, например, для моделирования целых чисел, потому что это слишком дорого.
Гораздо дороже говорить о проблеме, когда не знаешь ее границ.
Поэтому обычно люди используют теорию битовых векторов фиксированной длины, рассуждая о целых числах или даже символах.
Другая очень распространенная теория — это теория вещественной целочисленной арифметики и, в частности, линейной целочисленной арифметики.

Людям очень нравится эта теория, потому что она обеспечивает эффективную аргументацию, но она не очень хороша, когда вы спорите о программах, потому что именно здесь вас действительно волнуют проблемы переполнения.
Но эта теория широко используется для многих вещей.
Другая теория, которая часто используется, — это теория неинтерпретируемых функций.
Что означает эта теория? 
Это означает, что у вас есть определенная формула.
В этой формуле вы знаете, что вызываете функцию, но ничего не знаете о функции, кроме того факта, что если вы введете в нее какие-то входные данные, вы получите тот же результат, что и выходные данные.
Оказывается, это очень полезно при рассуждениях о таких вещах, как использование кода с плавающей запятой, моделирование, синусы, косинусы, квадратные корни.
Подробно рассуждать о таких вещах может оказаться очень трудоемким и дорогостоящим занятием.
Но использование этой теории позволяет вам сказать: «Послушайте, меня не волнует, что делает синусоидальная функция.
Мне все равно, что именно это даст в результате.
Мне просто нужно знать, что если я вызову функцию синуса в разных местах программы с определенными входными данными, я получу тот же результат, что и выход. Мне этого вполне достаточно, чтобы рассказать о своей программе».
И поэтому наиболее распространенными операциями при анализе реальных систем являются битовые векторы, работающие с целыми числами, логами и указателями.
Фактически, указатели часто представляются целыми числами, потому что иногда указателям не присваиваются битовые векторы.
Но иногда вам придется это сделать, и тогда вы больше не сможете использовать целые числа.
Итак, мы рассмотрели, что может сделать для вас решатель SMT. Как это на самом деле работает? Что внутри них заставляет их работать? В действительности, решатели SMT полагаются на нашу способность решать логические проблемы выполнимости SAT, способность рассматривать проблемы, включающие только чистые логические ограничения и логические переменные, и сообщать нам, будут ли значения, присвоенные этим логическим переменным, обеспечивать запуск программы или нет. .
Именно этому учат студентов уже много-много лет, говоря, что это на самом деле NP-полная задача, и в тех случаях, когда что-то сводится к SAT, не стоит этого делать.
Но оказывается, что у нас на самом деле есть очень хорошие решатели SAT. Итак, я расскажу вам основную идею того, как работают решатели SAT. Он берет все ваши ограничения на логические переменные и помещает их в базу данных.
Возможно, вам будет сложно разглядеть маленькие буквы на экране, но это все, что я могу сделать.

Я буду комментировать и говорить об этом по ходу дела, а позже выложу слайды, чтобы вы могли увидеть, что там происходит.
Итак, здесь, в задаче SAT, у нас есть все эти переменные, представляющие логические неизвестные, верно? Мы хотим знать, возможно ли, чтобы X было истинным (X = TRUE), Y было истинным, а Z было истинным.
Это наши неизвестные.
При этом все ограничения имеют нормальную конъюнктивную форму.
Это означает, что все наши ограничения имеют вид либо X1 = true, либо X2 = true, либо X3 = true.
В этой форме у нас есть все наши ограничения, которые говорят, что либо X1 истинно, либо X2 ложно, либо X3 ложно.
Вы, наверное, помните из дискретной математики, что любую булеву формулу можно представить в нормальной конъюнктивной форме.
Это означает, что любое представление, которое вы используете для представления логических формул, можно очень легко преобразовать в этот формат. Итак, у нас есть база данных с множеством ограничений такой формы.
Решающая программа SAT случайным образом выберет одну из этих переменных, скажем, X1. И он скажет: «Почему бы не установить для X1 значение true? Я ничего не знаю об этих ограничениях, поэтому могу предположить, что это правда».
И тогда произойдет следующее: у вас появятся ограничения, которые, например, заявляют, что либо X1 является ложным, либо X7 является истинным.
Итак, если вы знаете, что X1 истинно, и вы знаете, что либо X1 ложно, либо X7 истинно, что вы знаете о X7? Аудитория: это должно быть правда! Профессор: да, это должно быть правдой.
Потому что иначе это ограничение не будет выполнено.
Итак, теперь вы распространили это значение от X1 до X7. Предположим, вы теперь выбрали другую случайную величину, например X5. 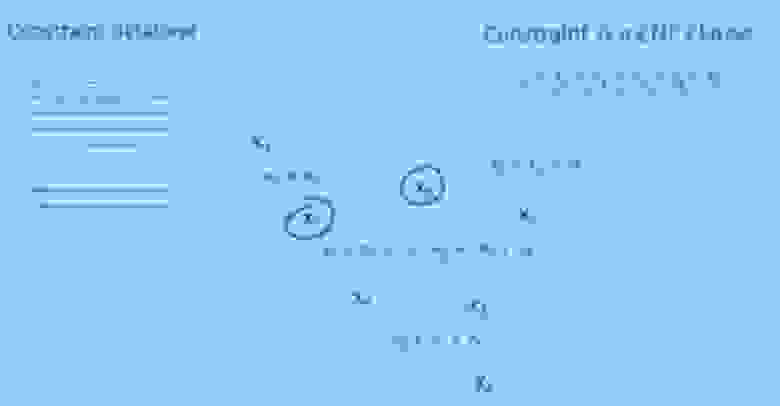
Теперь предположим, что у вас есть ограничение, которое гласит, что либо X7 является ложным, либо X6 является истинным, либо X5 является ложным.
Итак, у меня X5 = true и X7 = true. Это означает, что X6 теперь также должно быть правдой.
Потому что в противном случае это ограничение будет нарушено.
Таким образом, система приходит к выводу, что X6 должно быть правдой, и продолжает процесс, выполняя доступные проверки и просматривая все доступные предложения.
Система проверяет, есть ли другие вещи, которые подразумеваются имеющимися у нее проверками.
И он следует этим значениям до тех пор, пока не произойдет одно из двух.
Во-первых, вы продолжаете следить за последствиями и пробуете случайные вещи, и в конечном итоге вы установите значение для каждой переменной, ни разу не столкнувшись с противоречием.
Значит, вы все сделали правильно.
Во-вторых, вы сталкиваетесь с противоречием, а затем возвращаетесь к условию, которое сделало X4 истинным, исключая условие, которое сделало X4 ложным.
Но есть одно правило булевой алгебры, которое должен знать каждый: переменная не может быть одновременно истинной и ложной.
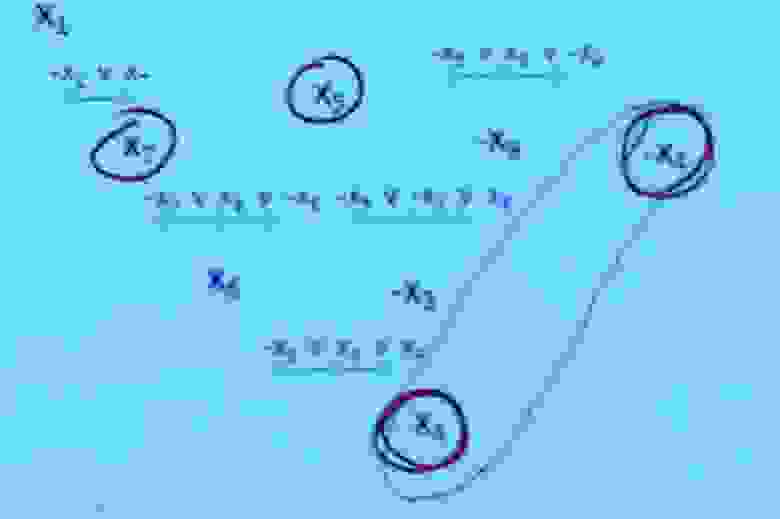
И там написано, что вы столкнулись с противоречием, вы явно сделали что-то не так в одном из этих случайных заданий, которое пытались выполнить.
Давайте проанализируем это противоречие и выясним, какие задачи привели к этому противоречию.
Исходя из задач, которые привели к данному противоречию, придумаем новую коллизионную оговорку, обобщающую это противоречие.
Что произойдет, если X1 ложно, X5 ложно и X9 тоже ложно? По сути, это основано на том, что я узнал из этих случайных заданий, в ходе которых я обнаружил, что одна из этих вещей должна быть правдой, что не может быть так, чтобы X1 было истинным, X5 — истинным, а X9 — ложным, этого не может быть.
Я знаю, что этого не может произойти, потому что, когда я попытался это сделать, все сорвалось, и я завершил программу из-за противоречия.
И вот решатель SAT пытается выполнять случайные задачи, проверяя, как они выполняются.
Когда он сталкивается с несоответствиями, он анализирует набор последствий, которые привели к этим несоответствиям, и в конечном итоге генерирует новое ограничение, которое гарантирует, что решатель никогда больше не столкнется с этим конкретным противоречием, этой конкретной проблемой.
Таким образом, мы можем думать о решателе SAT как о «черном ящике», который дает логическое ограничение и может сказать, удовлетворительно оно или нет. Решатели SMT созданы на базе лучших решателей SAT. Они могут применять возможности решателей SAT для решения NP-полных задач с помощью специфичных для предметной области рассуждений о поддерживаемых теориях.
Чтобы получить представление о том, как это работает, предположим, что у вас есть такая формула.

Возможно ли это? Можем ли мы найти для него удовлетворительный тест? Решатель SMT может выделить часть этой формулы, которая требует рассуждений в теории целых чисел.
Мы используем логические структуры для разделения формул.
Так мы получаем формулы F1, F2, F3 и F4. 
Это чисто логическая, булева задача – могу ли я найти для этого удовлетворительную задачу? Решатель SAT может сказать: «Да, я могу найти что-то, что решит эту задачу, сделав F1 = true, F2 = true и F3 = true».
Это удовлетворяет спецификации булевой формулы.
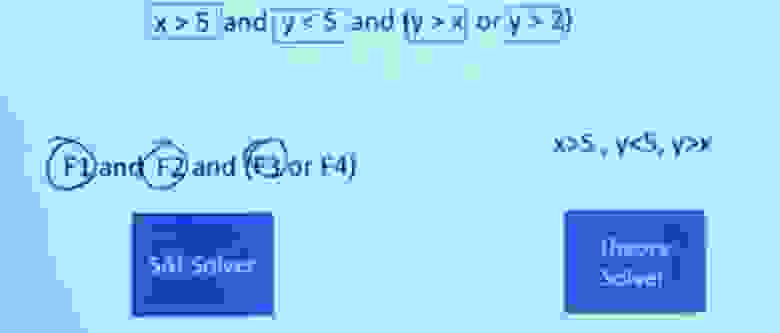
\
Итак, теперь у нас есть вопрос, который мы можем задать решателю, специфичному для предметной области, в данном случае это просто решатель линейной арифметики.
Итак, мы можем пойти к решателю линейной теории и сказать: «Решатель SAT утверждает, что это разумное задание, и что если я смогу заставить это задание работать, то моя формула будет удовлетворена».
Могу сказать, что F1 — это X > 5, F2 — это Y. < 5, and F3 is Y > X. Итак, я могу спросить решателя SAT, можно ли получить X и Y так, что X > 5, Y < 5, and at the same time Y would be > ИКС? Это вопрос чисто линейной арифметики, здесь нет никакой булевой логики.
И каков ответ на этот вопрос? Нет. Одновременно выполнить эти условия невозможно.
Итак, существуют традиционные методы решения линейных задач.
Симплекс-метод можно использовать, например, для решения систем линейных неравенств.
Существует множество методов решения систем линейных неравенств.
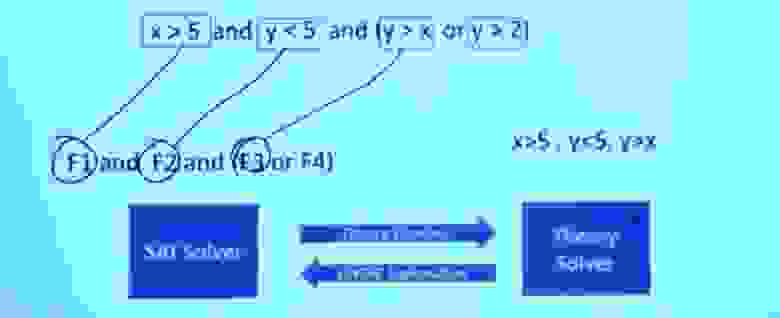
Итак, решатель SAT отправляет теоретические вопросы решателю по теории.
Дело в том, что решатели теории знают все об этих задачах и могут дать точный ответ на вопрос, сработают ли эти условия.
В этом случае теоретический решатель обрабатывает запрос, обнаруживает, что это назначение условий не может работать, возвращается к решателю SAT и говорит: «То, что вы сделали, не сработает»! Но он не просто говорит «да» или «нет», он объясняет, почему что-то не работает. Из того факта, что эти формулы не работают, решатель теории делает вывод, что F1, F2 и F3 не могут существовать одновременно, и сообщает решателю SAT, что эти 3 формулы являются взаимоисключающими.
Итак, теперь у нас есть часть информации, которую я могу передать решателю SAT и спросить его: «Эй, можете ли вы дать мне решение, которое удовлетворяет не только ограничению, которое у нас было в начале, но и новому ограничению, которое обнаружила ТеорияЭ» решатель"?
Есть ли какая-то другая цель, которая теперь удовлетворяет обоим этим ограничениям? 
Поэтому мы отбрасываем исходное ограничение X > 5, Y < 5, Y > Х, нас это больше не волнует. 
У нас есть новое ограничение, которое мы можем установить для нашего решателя теории — X > 5, Y. < 5, Y > 2. Мы можем сделать Y равным 3, а X равным 6, и тогда это сработает. Теперь у вас есть задание, которое теоретически удовлетворяет формуле и логической структуре этого задания.
И при этом система может вернуться и сказать: «Да, вот работа, которая удовлетворяет всем вашим ограничениям».
Это взаимодействие между решателем теории и решателем SAT. На самом деле это означает способность рассуждать об очень, очень больших и очень сложных логических формулах.
Именно это делает возможной символическую казнь.
Теперь мы рассмотрим следующий вопрос — как перейти от программы к ограничениям, которые мы можем предоставить решателю SMT. Аудитория: Является ли построение решателя SMT NP-полной задачей или нет? Профессор: Решатель SMT, по сути, сам по себе является канонической NP-полной задачей.
Но большинство решателей в наши дни также поддерживают некоторые теории, которые совершенно неразрешимы.
Аудитория: Как следует подойти к этой проблеме в вашей системе? Профессор: ну и в итоге вы получите ограничение, созданное из этой программы.
Вы собираетесь передать его решателю SMT. А то, что это NP-полные задачи, или то, что они неудовлетворительны, означает, что если вам повезет, вы получите ответ за считанные секунды.
Но если вам не повезет, это может занять больше времени, чем потребовалось для создания Вселенной.

Аудитория: Бывает ли так, что проблемы с линейной системой не сдаются на SAT? Профессор: Да, это действительно происходит. Однако доступные инженерные инструменты означают, что это становится все менее и менее распространенным.
Мы не решаем случайные задачи SAT, мы не решаем полностью случайные задачи с битовыми векторами.
Мы решаем задачи, имеющие определенную структуру, чтобы человек мог посмотреть на нее и иметь некоторую уверенность, что это сработает. Мы пытаемся создать в его голове какие-то аргументы, почему это сработало.
И решатели SAT используют эту структуру.
В вашей задаче может быть миллион логических переменных, но на самом деле большинство этих переменных очень зависят от значений друг друга.
Таким образом, число степеней свободы в задаче на самом деле намного меньше, чем предполагают миллионы переменных.
Аудитория: Вы говорите, что это не экзаменационный вопрос, а реальная жизнь.
Поскольку кто-то создал эту систему, она должна работать и иметь смысл.
Так что это, вероятно, не будет одной из тех ненужных теоретических тиражей.
Профессор: вот и все.
Поэтому на практике, когда вы используете этот инструмент, вы всегда устанавливаете таймауты.
По сути, все происходит потому, что экспоненциальность не означает, что вы не можете этого сделать.
«Экспоненциальность», то есть когда одна функция ограничена другой функцией, просто означает, что существует кирпичная стена, перед которой эти вещи будут работать, и они действительно будут работать очень быстро.
«Экспоненциальность» работает в обоих направлениях.

По мере того, как вы отходите от этой стены, ситуация очень быстро обостряется, но по мере того, как вы приближаетесь к меньшим или более простым проблемам, эти проблемы также ускоряются очень, очень быстро.
Это означает, что многие проблемы заканчиваются очень быстро.
А потом наступает таймаут проблем.
Смысл в том, чтобы спроектировать вещи таким образом, чтобы среди тех проблем, которые быстро заканчиваются, были проблемы, приносящие практическую пользу.
Это проблемы, которые указывают вам на уязвимости безопасности в вашей системе, ошибки, пути, которые вы, возможно, не исследовали раньше, или входные данные, которые сломают ваши пути, если вы не исследовали их заранее.
Итак, мы знаем, как перейти от формулы, от набора ограничений, к ответу, который либо говорит: «Да, у этой формулы есть решение, и вот оно, это и есть решение».
Или скажет: «Эта формула неудовлетворительна, потому что нет входных данных, удовлетворяющих вашим задачам».
Так как же нам получить формулу из программы? Когда делаешь символическую экзекуцию, ты подходишь к ветке и не знаешь, в каком направлении она пойдет. Есть два варианта того, что вам следует делать в этом случае.
Один из них — сделать то же, что мы сделали в предыдущем примере, то есть взять и рассмотреть обе ветви одновременно и собрать выходные данные, полученные в результате выполнения обеих ветвей программы.
Это стратегия, которая часто используется, когда вы пытаетесь получить очень надежные гарантии.
Но эта стратегия не очень хорошо работает с современными решателями и SMT-решателями.
Часто люди предпочитают исследовать только один путь за раз.
А это означает выбор этого пути для вашей программы и создание формулы для этого конкретного пути.
То есть вы сообщаете этой формуле: «найдите мне входные значения, которые следуют по этому пути и удовлетворяют моему ограничению, или которые нарушают мои свойства, или выходят за границы буфера, или указывают на нулевой указатель функции».
И если один путь оказывается неправильным, вы пробуете другой путь, затем следующий путь и так далее.
Потому что вы можете исследовать только один путь за раз.
Именно об этой стратегии мы сейчас и поговорим.
Немного проще описать, как это сделать.
Допустим, у нас на экране изображена такая программа.
Кстати, я изменил схему представления — теперь программа не выглядит как блок инструкций, я представил ее в виде графа потока управления.
Все ли здесь знакомы с графом потока управления? Это просто представление программы, которое делает ветки более явными.

Итак, давайте выберем путь, пусть это будет правая ветвь, которая начинается с t=0 и заканчивается утверждением false. 
Мы хотим знать, возможен ли этот путь, может ли программа следовать по этому пути? Для этого нам нужно взять две вещи: среду, отслеживающую символьные значения различных переменных, и среду для ограничений.
Эти ограничения по существу будут отслеживать все связи между переменными, а также любые сделанные предположения, независимо от того, были ли эти предположения сделаны в начале или исходили из ветвей, по которым выполняется программа.
В этом случае, когда мы начинаем выбранный путь, мы получаем значение t = 0, поэтому наше состояние — это x, y и 0. И на данный момент у нас нет никаких ограничений, потому что их не было в начале.
Итак, мы можем следовать выбранному пути только в том случае, если X больше Y.
Итак, нашим первым ограничением будет X > Y. 
55:00 мин.
Курс MIT «Безопасность компьютерных систем».
Лекция 10: Символическая казнь, часть 3 Доступна полная версия курса Здесь .
Спасибо, что остаетесь с нами.
Вам нравятся наши статьи? Хотите увидеть больше интересных материалов? Поддержите нас, разместив заказ или порекомендовав друзьям, Скидка 30% для пользователей Хабра на уникальный аналог серверов начального уровня, который мы придумали для вас: Вся правда о VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps от 20$ или как правильно раздать сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40 ГБ DDR4).
VPS (KVM) E5-2650 v4 (6 ядер) 10 ГБ DDR4 240 ГБ SSD 1 Гбит/с бесплатно до декабря при оплате на срок от шести месяцев и более вы можете заказать здесь .
Dell R730xd в 2 раза дешевле? Только здесь 2 x Intel Dodeca-Core Xeon E5-2650v4 128 ГБ DDR4 6x480 ГБ SSD 1 Гбит/с 100 ТВ от 249 долларов США в Нидерландах и США! Прочтите об этом Как построить корпоративную инфраструктуру класса, используя серверы Dell R730xd E5-2650 v4 стоимостью 9000 евро за копейки? Теги: #информационная безопасность #программирование #ИТ-инфраструктура #Анализ и проектирование систем #SMT #Символическое исполнение #Символическое исполнение #Символическое исполнение #Теория массивов TOA #Теория массивов TOA #Теория неинтерпретируемых функций #Теория неинтерпретируемых функций #Решатели SAT #Решатели SAT
-
Видеоархив Youtube Вырос До 45 Терабайт
19 Oct, 24


