Космология. Подробный Анализ Решения Фридмана

Полностью и достаточно подробно, но без пояснений, хорошо описано здесь (pdf) .

Я.

Представим себе одномерное пространство



, с натянутой внутри него осью



, равномерно изогнутый: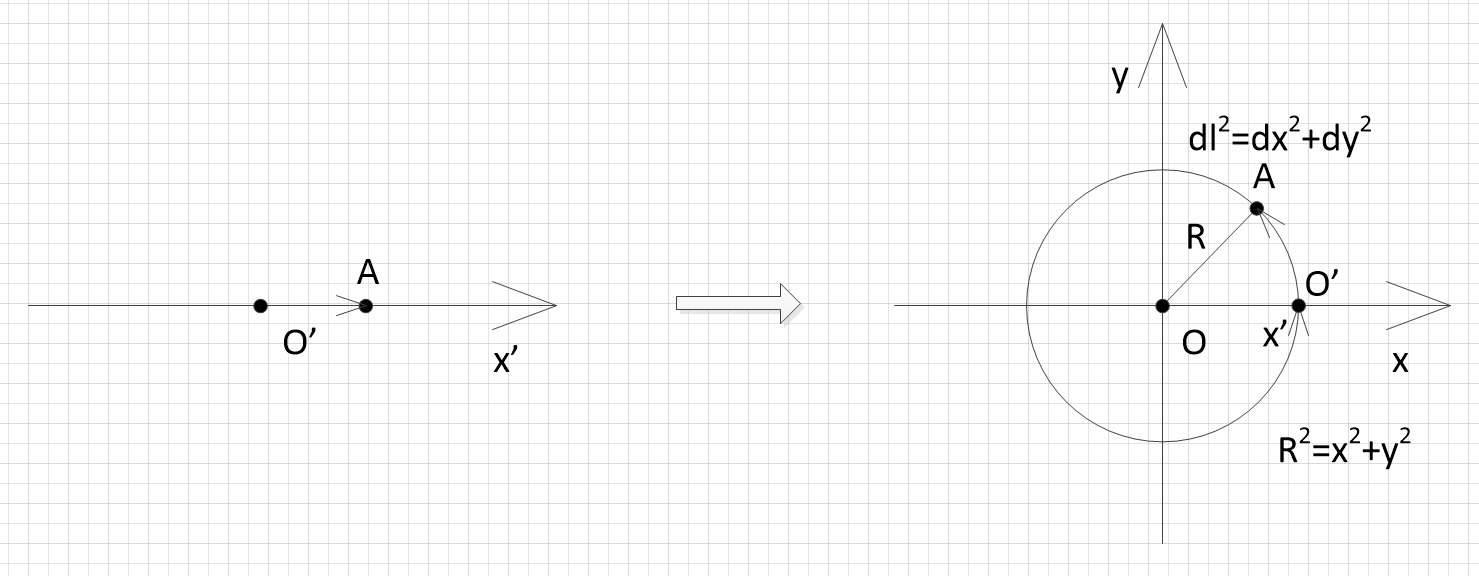



Можно сказать, что пространство



— одномерная гиперповерхность постоянной кривизны в двумерном пространстве (x,y).

Зададим произвольную точку



в космосе



, то, с одной стороны, длина движения от точки А до любой стороны пространства



определяется по формуле (1):



Где



— координаты в декартовой системе координат, сдвинутые относительно



, то есть имеющие начало О вне рассматриваемого пространства.

С другой стороны, кривизна



характеризуется радиусом R, который определяется формулой (2):



Продифференцируем (2), чтобы получить взаимозависимость скоростей изменения координат



И



:



.

Как будто раньше



был нулевым.

Если пространство имеет положительную кривизну, длина имеет отклонение в зависимости от



.

Множитель до



в этом случае



.

Для отрицательной кривизны знак множителя необходимо изменить на отрицательный (



).

Вы можете представить себе все три случая следующим образом:



Чем дальше мы движемся в таком пространстве



при постоянном радиусе кривизны



, тем хуже (мы проходим все меньшее расстояние) мы получим его в сферическом пространстве, без изменений в плоском пространстве, и лучше (большее расстояние) в гиперболическом пространстве.

II. Давайте расширим пространство



к трехмерному (x,y,z).

Будем считать, что радиус его кривизны



идентична в каждой точке, как если бы это была поверхность 3-сферы - все три оси скручены как ось



, образуя 3-сферу радиуса



.

Проделаем те же операции, что и для одномерного варианта, чтобы получить уравнение движения в трехмерном пространстве (3): Детальный вывод пространственной составляющей в декартовых координатах



(1)



дифференцировать и выразить dw:











подставить в (1):



Красным цветом обозначена «изогнутая» часть, отличающая метрику FRW от плоской метрики.

Пространства Минковского .

В этом представлении хорошо видно, что последний «искривленный» член не может быть разделен непосредственно по осям, что, в свою очередь, приведет к появлению недиагональных членов метрического тензора, а это существенно затруднит дальнейшие расчеты.

(или сделать это невозможно, я не пробовал).

Поэтому нужно искать обходной путь.

Необходимо найти такое координатное представление, чтобы кривизну можно было выразить отдельно для каждого базисного вектора.

Сферические координаты отлично подходят для отдельного представления кривизны, поскольку вторая и третья координаты являются углами и зависят от кривизны линейно, а не квадратично, как декартовы координаты.

Что при качественно идентичной декартовой первой координате все же позволяет выразить кривизну удобным образом (4), так что вся она «схлопывается» в знаменатель множителя по первой координате в виде компонента



: Подробно переход к сферическим координатам и получение представления



красным здесь снова «кривая» часть:























Где



— линейная координата (первая),



— угловые координаты (вторая и третья),



; и получается, что члены метрического тензора, выделенные цветом (по очереди – красным, зеленым, синим):











это диагональные члены метрического тензора.

III. Все? Нет. Заменим первую координату



, выражая его через радиус кривизны:



;



.

Размерность оси времени равна



(скорость света), при которой



(светоподобный интервал равен нулю).

Я.

Все начинается с того, что некая точка (частица) движется в отсутствие внешних сил (ускорение равно нулю) в декартовых координатах.

:



Где



.

Однако если перейти к сферическим координатам



, это простое тождество больше не будет работать напрямую.

Надо сначала цивилизованно зайти по координатам



:



Красный — члены матрицы преобразования ( якобианы ):



Осталось еще раз дифференцировать по времени:



Мы получаем:



Таким образом, получено условие отсутствия ускорения в сферических координатах.

Нам остается только привести его к более удобному виду.

В левом члене якобиан остается нетронутым из-за красоты дифференцирования по частям; в правом члене берется производная якобиана.

Видно, что если умножить последнее представление на перевернутый якобиан, мы «освободим» ускорение по одной из координат (зеленого цвета), приведя его к исходному виду в декартовой системе:



А вот этот чудовищный пурпурный цвет, в результате которого получается правильный член в качестве множителя для производных координат



, и имеется символ Кристоффеля второго рода (6):



То есть символы Кристоффеля характеризуют метрику тем, насколько ее форма искажает значение каждой из координат при перемещении определенной точки относительно начала координат. Еще проще Символы Кристоффеля – множители базисных векторов, соответствующие их переносу в пространстве, заданном метрикой.

II. Несомненным преимуществом предыдущего способа представления коэффициентов связности является то, что он одновременно дает понятие уравнения геодезических.

Но, возможно, кому-то будет понятнее вариант представления символов Кристоффеля через дифференцирование базисных векторов.

В книге очень четко написано Ю.

А.

Аменадзе «Теория упругости» (pdf, пункт 4) .

Дело в том, что изменение метрики от точки к точке означает изменение базисных векторов в этих точках.

Изменение базисного вектора удобно выразить через его производную.

Поскольку в криволинейной системе координат базисными векторами являются функции, аргументом которых является положение точки, то производные, взятые непосредственно по координатам, будут ненулевыми (7):



Множитель вектора, полученного в результате такого дифференцирования, будет символом Кристоффеля второго рода.

Ясно, что



является множителем базисного вектора



, соответствующий его кривизне при перемещении базисного вектора



вдоль оси



:



— координата базисного вектора, в котором находится коэффициент;



— координата переменного базисного вектора;



— координата, по которой отслеживается изменение.

То есть для декартовых координат, в которых перемещение точки не влияет на размер базисных векторов, все символы будут равны нулю.

Это так же очевидно, как и то, что при перемещении точки в сферических координатах изменяется значение базисных векторов угловых величин (второй и третьей координат).

В каком-то смысле это компромисс между линейностью и кривизной.

В метрике FRW, отличающейся от сферической наличием множителя по первой координате, вследствие этой особенности перенос базиса по первой координате также приведет к ее изменению.

Коэффициенты связности можно рассчитать по формуле из их определения.

Например



В которой:



Отсюда:



Собственно, пурпурный цвет – это и есть необходимый коэффициент:



Хитрость в том, что после дифференцирования нужно вынести нужный базисный вектор, а остальное уплотнить.

Но это удобно не во всех случаях, поэтому выведем универсальную формулу.