Оверклокеры, вооруженные жидким азотом, неоднократно показывали, что современные чипы могут стабильно работать на частотах, многократно превышающих номинальные, обеспечивая соответствующий прирост производительности.
Однако прогресс в области «гигагерцовой гонки» давно и надежно остановился.
Первый Pentium 4 с частотой более 3 ГГц появился еще в 2002 году, почти 10 лет назад. За последние годы нормы технологического процесса снизились со 180 до 32 нм, но даже это не позволило существенно увеличить стандартные рабочие частоты.
Все сводится к огромному тепловыделению цифровых логических элементов.
В основе «проблемы тепловыделения» лежит глубокая связь информации и термодинамической энтропии, а также второй закон термодинамики, запрещающий уменьшение полной энтропии замкнутой системы.
Любой расчет, уменьшающий информационную энтропию, должен приводить к увеличению термодинамической энтропии, то есть к выделению тепла.
Рольф Ландауэр показал в 1961 году [ PDF ] что уничтожение одного бита информации должно приводить к выделению не менее k∙T∙ln 2 джоулей энергии, где k — постоянная Больцмана, а T — температура системы.
Эта энергия сама по себе невелика: при Т=300К она составляет всего 0,017 эВ на бит, но в пересчете на процессор в целом полная энергия уже вырастает до значений порядка одного Джоуля за каждую секунду работы, то есть порядка одного Ватта [ Компьютерра №538 ].
На практике этот теоретический минимум помножается на ненулевое сопротивление и другие недостатки реальных полупроводников.
В результате мы получаем процессоры, превосходящие утюги по тепловыделению.
Уничтожение информации в современных процессорах происходит постоянно и на самом низком уровне, в вентилях «И-НЕ», которые являются «строительными блоками» любой современной цифровой схемы.
Принимая на вход два бита, гейт выдает результат только из одного бита, из которого, конечно, невозможно восстановить значения исходных аргументов.
Точнее, каждое вычисление вентиля И-НЕ снижает энтропию информации на 1,189 бита и, соответственно, рассеивает не менее ~0,02 эВ тепла.
Аналогичная ситуация и с непопулярной сегодня формулой «ИЛИ-НЕ».
Не лучше ситуация и с ячейками памяти, любая запись в которые приводит к уничтожению предыдущих значений.
Для программиста старые данные просто «теряются», но на физическом уровне законы сохранения заряда и энергии не позволяют им потеряться «просто так».
На самом деле старая информация не уничтожается, а рассеивается в пространстве в виде тепла и паразитного излучения.
Уже более 30 лет известен метод организации вычислений без уничтожения информации, не подпадающий под принцип Ландауэра и позволяющий создавать теоретически энергоэффективные процессоры.
Этот метод называется консервативной, или «сохраняющей» логикой.
К сожалению, так и не удалось создать для него компактную физическую реализацию в кремнии; известен только способ реализации на МОП-транзисторах с плохо миниатюризированными индуктивностями.
С другой стороны, такой подход естественен для большинства типов квантовых компьютеров, в том числе оптических (модель Бениоффа и др.
).
С годами выяснилось, что консервативная логика оказалась полезной математической абстракцией даже без реализации «аппаратно»: на ее основе создаются блочные клеточные автоматы, которые очень удобно использовать при решении задач «с ограниченными ресурсами».
.
Эта отрасль математики сейчас очень активно развивается, и, возможно, через десять лет блочные клеточные автоматы будут среди программистов еще более известны, чем обычные.
«Взмахом крыла бабочки», повлекшим за собой появление этой статьи, стал вопрос, заданный товарищем Плаховым, «как это по-русскиЭ», ответа на который не знает даже Яндекс.
Если не считать упомянутой выше статьи в «Компьютерре» за 2004 год, на русском языке вообще нет никакой информации о консервативной логике – что тем более обидно, что ее теоретические основы были заложены великими советскими физиками Ландау и Лифшицем ровно 50 лет назад, в 1961. Чтобы хоть немного ликвидировать этот пробел, с одной стороны, и «не затыкать кляп», с другой, предлагаю вашему вниманию реферат (перевод основных тезисов) фундаментальной статьи о консервативной логика Дуарда Фредкина и Томассо Тоффоли, опубликованная в журнале «Теоретическая физика» № 21 за 1982 год. (Фредкин, Эдвард и Тоффоли, Томассо, «Консервативная логика», Int. J. Theor. Phys. 21 (1982), 219 –253; PDF ).
В данной статье раскрываются все основные моменты, касающиеся физики, логики и схемотехники систем, основанных на консервативной логике.
Консервативная логика Консервативная или консервационная логика — это математическая модель организации вычислений, основанная на двух фундаментальных физических принципах: обратимости процессов и законах сохранения.
1. Физическая основа
(Нумерация разделов реферата не совпадает с нумерацией частей статьи – ок.переулок ) Любой расчет, независимо от того, как он выполняется, человеком или машиной, должен подчиняться определенным физическим законам.
В частности, скорость распространения информации ограничена скоростью света, а количество информации в конечной системе также должно быть конечным.
Есть и более сложные ограничения.
Все физические законы можно разделить на динамические и статистические.
Первые описывают поведение отдельных объектов в полностью определенных микроскопических системах и позволяют – в классической механике – точно предсказать результат любого эксперимента.
Когда объектов слишком много, чтобы пересчитать каждый из них, применяются статистические законы, описывающие среднее поведение однородных объектов в макросистеме.
Они позволяют оценить общую картину, но не дают возможности предсказать поведение конкретного объекта.
На микроуровне наш мир обладает различными фундаментальными однородностями и симметриями, многие из которых приводят к появлению «законов сохранения» на макроуровне.
Таким образом, однородность времени обеспечивает выполнение закона сохранения энергии, однородность пространства обеспечивает закон сохранения импульса, а изотропность пространства (симметрия направлений) приводит к закону сохранения момента импульса.
Все динамические фундаментальные физические законы обратимы в смысле замены координат обратными.
Удар в бильярде можно отменить, если бросить все шары в противоположном направлении.
С другой стороны, статистические физические законы подчиняются принципам термодинамики и необратимы, если не повернуть вспять стрелу времени; разбитую вазу никогда не собрать из осколков.
В частности, традиционная вычислительная модель, работающая на макроуровне и основанная на вентилях И-НЕ или ИЛИ-НЕ, необратима.
Любой расчет в такой модели требует энергетических затрат в соответствии с принципом Ландауэра.
При любой организации вычислений цифровая информация физически представляет собой пронумерованные устойчивые состояния любых систем.
Примечание переулок : Статья предназначена для физиков, поэтому авторы не приводят иллюстраций очевидных для физиков вещей.Хотя на самом деле эти состояния могут быть электрическими, оптическими и т. д., здесь и далее мы будем называть их «механическими», чтобы отличить их от термодинамических состояний.Последнее предложение как раз об этом: например, конденсатор ячейки памяти может находиться в двух логических состояниях — «заряженном» или «разряженном» (хотя, конечно, «физический» заряд конденсатора — величина практически непрерывная, а не логическое значение).
Стабильность этих логических состояний обеспечивается специальной электронной схемой регенерации, которая заряжает заряженные конденсаторы и разряжает разряженные.
При этом разница в энергии между «заряженным» и «разряженным» состояниями должна быть огромной по сравнению с уровнем теплового шума, иначе сохраненные значения могут быть повреждены.
Термодинамические состояния — это степени свободы отдельных атомов и молекул, составляющих вещество.
В одном грамме любого вещества содержится огромное количество, около 10 23 (число Авогадро), число таких степеней свободы, и учесть их можно только статистическими методами и законами.
Второй закон термодинамики гласит, что полная энтропия замкнутой системы не может уменьшаться.
Принцип Ландауэра устанавливает энергетические связи между информационной и термодинамической энтропией.
Многие алгоритмы приводят к уменьшению информационной энтропии, но такое уменьшение должно быть либо компенсировано увеличением термодинамической энтропии (тепловыделения), либо запрещено.
Соответственно, возможны два принципиально различных подхода к физической организации вычислений.
В «консервативном» или «сохраняющем» подходе для хранения информации выбираются механические состояния, для которых обмен энтропии с термодинамическими состояниями невозможен.
В такой системе должны быть запрещены любые операции, снижающие информационную энтропию, в частности операции уничтожения информации.
Поэтому все операции должны быть обратимыми.
Ландау и Лившиц показали, что в такой системе должны существовать некоторые инвариантные аддитивные величины, например заряды или моменты, «защищенные» законом сохранения, — только тогда переход «зарядов» в «температуру» и обратно будет невозможен.
Суммарный уровень этих величин, присутствующих в закрытой системе, будет величиной постоянной и не зависящей от процессов, происходящих в системе.
В отличие от консервативного, при обычном подходе «фон Неймана» расчеты изначально необратимы.
Чтобы удовлетворить второму началу термодинамики, должен существовать путь обмена энтропией и энергией между механическими и термодинамическими степенями свободы.
Такой путь должен быть односторонним (то есть необратимым), чтобы тепловые колебания не могли разрушить информацию, хранящуюся в механических состояниях.
Но, поскольку на микроуровне все процессы обратимы, добиться одностороннего потока энтропии можно лишь в том случае, если разность энергий между механическими состояниями на много порядков больше, чем между термодинамическими.
В современной вычислительной технике (по состоянию на 1982 г.
ок.
переулок ) разница составляет от 8 до 12 порядков.
Примечание переулок : представьте, что наша система состоит из W-образного стакана очень маленьких размеров и находящегося в нем шарика.Вся сегодняшняя вычислительная техника построена по второму, «необратимому» пути.Шарик имеет два устойчивых положения – внизу левой и правой половин стакана.
Это механические состояния, которые можно пронумеровать и в них можно хранить информацию.
Чтобы «записать» в стакан новую информацию, в смысле изменить положение шарика, нужно поднять шарик на холм в центре стакана, затрачивая на этот подъем определенное количество энергии.
Тогда по другую сторону стакана эту избыточную энергию надо забрать обратно или как-то погасить, иначе шарик будет колебаться вокруг положения равновесия с большой амплитудой.
Как бы ни был организован процесс отбора избыточной энергии, часть ее все равно превратится в тепло, но чем меньше «высота горки», тем меньше будут потери энергии.
Теперь представьте, что в реальной системе и шарик, и стакан испытывают постоянные тепловые вибрации.
Сила таких колебаний пропорциональна температуре.
Пока температура низкая, шар хотя и не всегда идеально находится в точке равновесия, но, по крайней мере, часто возвращается в нее.
Но по мере повышения температуры колебания усиливаются, и в какой-то момент мяч получает шанс самопроизвольно «перепрыгнуть» через горку.
Допускать этого нельзя ни при каких обстоятельствах, поэтому «скольжение» должно быть очень высоким – с неизбежно большими энергозатратами на его нормальное преодоление.
Необратимость специально заложена в базовые логические схемы, в p-n переходы транзисторов, и даже если вычисляемый алгоритм высокого уровня формально обратим, при выполнении на современных процессорах по крайней мере часть его отдельных шагов необратимы на самом низком уровне.
Необратимость также означает сильное выделение тепла, что ограничивает достижимую производительность.
2. Основные элементы консервативной логики
Вычислительные модели, основанные на консервативном принципе, должны использовать базовые логические элементы, удовлетворяющие определенным условиям.В частности, они должны быть обратимыми и сохранять те же самые аддитивные величины (заряды, моменты).
Из второго требования следует, что количество входов элемента должно быть равно количеству выходов, что, в свою очередь, означает строго взаимно-однозначную функциональную композицию.
Примечание переулок : В обычном схемотехнике выход одного логического элемента может быть подключен к входам нескольких других элементов («разветвление»).Консервативная логика основана на двух элементах — повторителе и вентиле Фредкина.В консервативном схемотехнике один выход должен приходиться точно на один вход следующего элемента; Для ветвления необходим специальный логический элемент (см.
ниже).
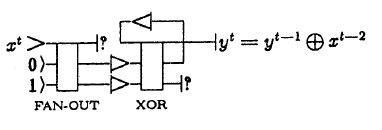
Репитер (единичный провод; буквально «элементарный проводник») просто повторяет на выходе сигнал, подаваемый на его вход, с задержкой в 1 такт. Именно скорость работы повторителей определяет тактовую частоту схемы.
Формально функция репитера выражается так:
й т = х т-1
Символ: 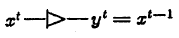
Повторитель может выполнять функции как хранения (будучи замкнутым на себя), так и передачи информации внутри схемы, но его основная задача – синхронизировать сигналы с тактовым генератором.
Обратный к репитеру элемент – это тот же репитер, но направленный в противоположную сторону.
Значения на выходах повторителей при определенном такте полностью описывают внутреннее состояние цифровой схемы консервативной логики, то есть выходы повторителей являются переменными состояния такой схемы.
Сумма значений на выходах повторителей будет такой же аддитивной запасенной величиной («общий заряд»), а для закрытой системы – постоянной величиной.
Общее количество повторителей в цепи можно рассматривать как количество степеней свободы этой цепи.
Повторители отдаленно похожи, но далеко не эквивалентны элементам задержки в обычных схемах «фон Неймана».
клапан Фредкина представляет собой устройство с тремя входами u, x1, x2 и тремя выходами v, y1, y2, реализующее функцию управляемого «перекрытия» («пересечения») двух линий данных (см.
рисунок).
Выход v всегда такой же, как вход u. Когда u=1, выходы y1,y2 равны входам x1,x2; при u=0 y1=x2 и y2=x1 (см.
таблицу) 
Таблица истинности ворот Фредкина:
(u, x1, x2) => (v, y1,y2)
0,0,0 => 0,0,0
0,0,1 => 0,1,0
0,1,0 => 0,0,1
0,1,1 => 0,1,1
1,0,0 => 1,0,0
1,0,1 => 1,0,1
1,1,0 => 1,1,0
1,1,1 => 1,1,1
Клапан Фредкина является инверсным.
Таким образом, любая схема в консервативной логике представляет собой управляемый условный маршрутизатор сигналов, на выходах которого формируется определенная управляемая перестановка входных значений в предыдущих рабочих циклах.
3. Консервативная схема
В консервативной логике можно реализовать машину Тьюринга (Беннетт, 1973) и универсальный клеточный автомат (Тоффоли, 1980).Таким образом, консервативная логика позволяет решать любые вычислимые Чёрчом задачи.
Процесс реализации произвольных функций в консервативной логике очень похож на такой же процесс в традиционной логике.
Так же, как и в традиционной схемотехнике, при реализации некоторых функций используются константы — источники постоянных значений 0 или 1. С другой стороны, в результате вычислений можно получить не только требуемые результаты, но и побочные результаты, которые не нужны для дальнейшего использования в конкретном алгоритме.
Полученные побочные продукты называются «мусором» или «раковиной».
Поскольку в консервативной логике сигналы не появляются «из ниоткуда» и не исчезают «в никуда», невозможно просто отбросить строки с «лишними» результатами; их нужно утилизировать каким-то особым образом (рассеять в пространстве).
На рисунке показано условное обозначение блока расчета некоторой функции φ: 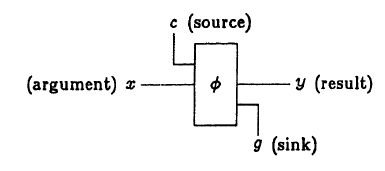
Вот как устроен блок" И ": 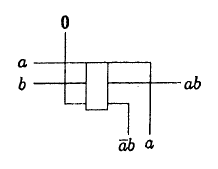
(обратите внимание, что один из приемников является копией аргумента)
На следующем рисунке показаны схемы реализации логических функций» ИЛИ "(а), " НЕТ "(группа разделитель сигнал 2а-а.
Последние два различаются лишь логической ролью выводов.
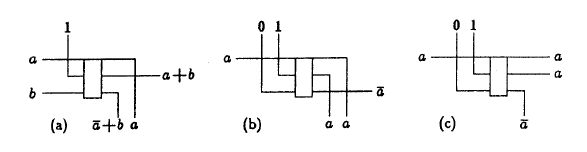
На следующей схеме показан простейший элемент памяти: триггер JK .
Знак вопроса указывает на слив, не имеющий никакого значимого значения.
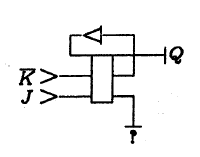
Ниже представлена более сложная схема: демультиплексор , посылая сигнал X по двоичному адресу A0, A1 на один из четырех выходов Y0 – Y3: 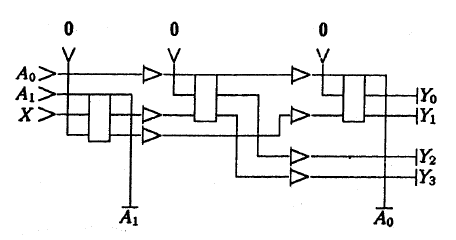
В консервативной логике можно реализовать любую схему из «обычной» логики.
Например, следующие три рисунка показывают реализацию однобитный последовательный сумматор : первое в обычной логике (в старых обозначениях), а второе и третье в консервативной логике.
При этом вторая схема собиралась путем простой подстановки замен в первую, а третья создавалась «с нуля».
На диаграммах показана разница между повторителями и элементами задержки: в консервативных схемах сигналы синхронизируются явно.
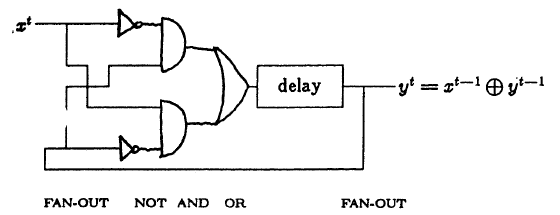
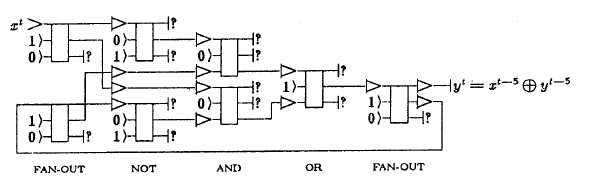
4. Проблема отходов
Практическая ценность консервативной логики, если она реализована, например, в квантовых компьютерах, полностью зависит от количества отходов, требующих переработки в реальных расчетах.Уничтожение сточных вод – это та же самая операция «высвобождения энергии», присущая обычным схемам.
Если каждый триггер процессора будет иметь свой сток, выигрыша в энергопотреблении не будет. Полностью избежать появления отходов невозможно.
Например, во многих реальных алгоритмах конечный результат представляет собой сумму некоторых чисел.
Но сама операция суммирования необратима, так как, зная только ее результат, невозможно определить исходные члены.
В универсальном процессоре, выполняющем поочередно множество различных программ и алгоритмов, такой «лишней» информации будет накапливаться слишком много, чтобы ее можно было просто отмахнуть.
Потребуется специальный «обменник энтропии», в который подаются результаты отходов.
В зависимости от типа вычисляемой функции возможны три сценария соотношения количества требуемых констант и стоков (см.
рисунок): 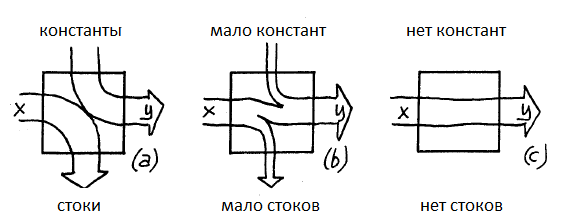
Третий, лучший сценарий возможен только в том случае, если вычисляемая функция f сама по себе обратима и подчиняется существующим законам сохранения.
Существует способ частично решить проблему стока и в то же время упростить генерацию констант, используя инвертированные схемы.
Под «инвертированной» мы подразумеваем схему, которая меняет заданную схему, то есть восстанавливает входы и константы из заданных выходов и стоков.
Поскольку все схемы в консервативной логике обратимы, то для инвертирования схемы достаточно просто поменять местами все повторители и вызвать входы выходами; или, что то же самое, отразить схему в зеркале (см.
рисунок).
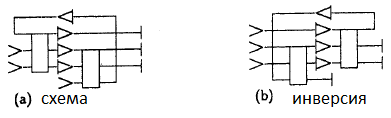
Прямая и инвертированная цепи могут быть соединены последовательно друг за другом.
Полученный таким образом элемент будет дублировать свои входы с большой задержкой, не требуя никаких констант и не создавая стоков, но где-то внутри него будут иметься результаты вычислений исходной функции (см.
рисунок).

Рассчитанные значения исходной функции можно «получить» «встраиванием» схемы «шпионских разветвителей»: 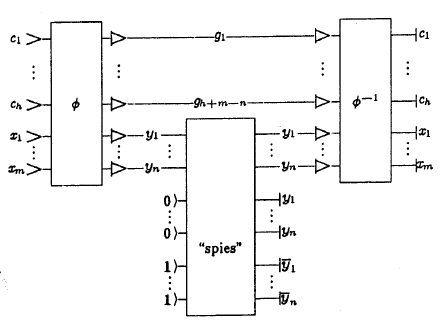
Для использования такой схемы еще необходимо предусмотреть константы (точнее, регистр-«блокнот», который необходимо один раз заполнить нужными нулями и единицами), а также правильно заполнить как выходной, так и выходной регистры.
Выходом такой схемы является а) копия аргументов, б) результат и в) инверсия результата — и если что-то из этого больше нигде не используется, то от них тоже придется избавиться.
Основное преимущество этого метода заключается в том, что количество ненужных строк пропорционально только размеру входного бита.
В то же время количество вентилей, необходимых для реализации большинства реальных функций в любой логике, растет примерно как экспоненциальная функция входной емкости.
В обычной схеме все вентили излучают тепло, в консервативной конструкции тепло выделяют только «сливные» вентили, поэтому при большой входной мощности польза должна быть огромной.
5. Модель бильярдных шаров.
В этой части представлена абстрактная физическая модель, в которой реализована консервативная логика.
Модель представляет собой плоскость, по которой бильярдные шары движутся без трения в строго заданных направлениях.
Скорости, допустимые направления и размеры шариков выбраны таким образом, чтобы в дискретные моменты времени, соответствующие тактам, шарики могли находиться только в небольшом наборе точек, образующих прямоугольную сетку, повернутую на 45' (см.
рис.
).
При попадании шариков в соседние точки между ними происходит упругое столкновение.
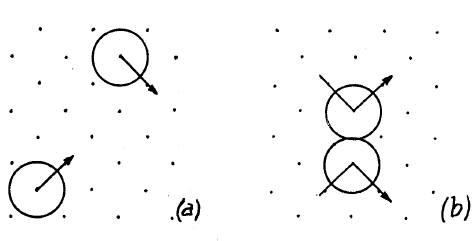
Логическая единица – наличие шарика, а ноль – его отсутствие.
Произвольную точку сетки можно объявить «воротами взаимодействия», если в ней пересекаются траектории двух шаров.
Направление выхода этих шариков зависит от наличия обоих: 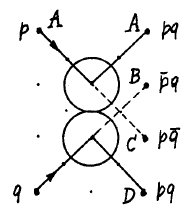
На плоскости можно установить неподвижные стены или зеркала.
С помощью зеркал можно вращать (а), сдвигать (б), задерживать и безопасно пересекать траектории (г) шариков.
Последний элемент (d) называется «нетривиальным кроссовером» и позволяет шарикам «как будто проходить сквозь друг друга».
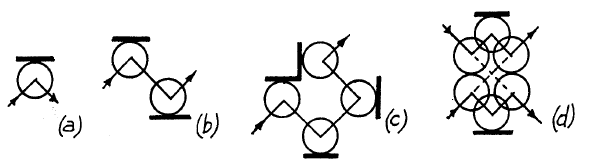
Возможно создание управляемых коммутаторов.
На рисунке показаны: структурная схема простого выключателя, обозначение обратного выключателю элемента, а также схема реализации простого выключателя.
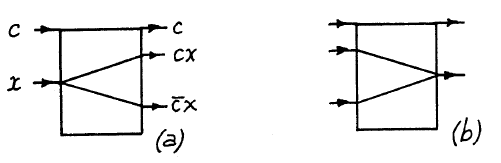
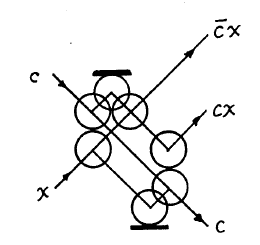
Наконец, из простых переключателей и нетривиального кроссовера (обозначаемого как «мост») можно сконструировать вентиль Фредкина (поворотные зеркала и задержки для наглядности не показаны): 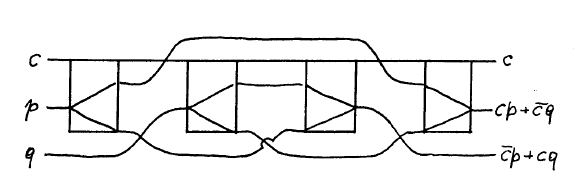
Что касается реальной физической реализации, то на роль шаров больше подходят молекулы газа, чем настоящие бильярдные шары, хотя ни один из вариантов так и не был реализован.
Основным преимуществом модели бильярдного шара является простота моделирования: благодаря специально подобранным углам и скоростям результаты всех столкновений можно рассчитать с помощью простых булевых функций, без использования чисел с плавающей запятой, дорогостоящих операций округления и т. д. Это позволяет быстро моделировать даже очень большие консервативные логические схемы на традиционных компьютерах.
6. «Трудные» вопросы о консервативной логике
1. Возможны ли произвольные вычисления в консервативной логике? Да, они возможны, консервативная логика полна по Тьюрингу.2. Существуют ли физические эффекты, к которым можно применить консервативную логику? Да, это можно реализовать на основе электронных элементов (дискретные элементы L/R/C плюс МОП-транзисторы) (на практике к 2011 году все останется только на бумаге и в лабораториях - ок.
переулок ) 3. Будет ли энергия, необходимая для утилизации отходов, превышать потенциальный выигрыш от перехода к консервативной логике? Полный ответ на этот вопрос нельзя дать без учета конкретной физической модели, но способ сокрытия сточных вод, описанный в пункте 4, оставляет очень высокую вероятность отрицательного (в смысле оптимистического) ответа.
4. Наконец, остается без ответа вопрос об устойчивости системы к малому шуму.
Вместо заключения (от переводчика)
Сам факт, что управляемо смешивая проводки в жгуте или кабеле между входом и выходом и не используя никаких других элементов, кроме «переходников» и повторителей, можно получить на выходе результат вычисления какой-либо функции по входу, далек от очевидный.Лежащая в основе вычислительная логика необычна, но в отличие от других полных по Тьюрингу математических абстракций, таких как алгоритмы Маркова, она выглядит очень высокотехнологичной и готовой к использованию в реальных процессорах.
Вполне возможно, что над чем-то подобным, с поправкой на чисто квантовые «фокусы», будут работать квантовые компьютеры.
Если объединить консервативную квантовую логику со сверхпроводящими соединениями, можно построить по-настоящему энергонезависимый компьютер.
Что ж, будущее покажет. Теги: #консервативная логика #квантовый компьютер #обратимые вычисления #обратимые вычисления #Системное программирование
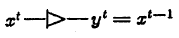
-
Ищем Угнанную Машину И Находим Ее Сами
19 Oct, 24


