Как Появились Регулярные Выражения?

Краткое предисловие Меня всегда интересовала история появления научных концепций.
Студент, изучающий новый предмет, сначала сталкивается с рядом безликих определений.
Некоторые из них остаются таковыми, другие привлекают внимание и со временем вырастают в полноценные объекты «картины мира».
В качестве недостижимого идеала такого стремления можно привести высказывание Литтлвуда о Рамануджан :

каждое натуральное число было его лучшим другом

Мне всегда было интересно не только освоить концепцию, но и понять, как она появилась.

За каждым определением всегда стоит личность.

Интересно понять, какие идеи лежали в основе той или иной концепции и почему новые определения были восприняты и поддержаны другими людьми с таким энтузиазмом, что остались в учебниках.

Ниже мы представим небольшое исследование такого рода, объектом которого является концепция регулярное выражение .

Нейронные сети Маккаллоха-Питтса

Удивительно, но основным мотивом введения понятия регулярного выражения стали нейронные сети.

Немного об истории понимания этого понятия.

Понятие нейронной сети возникло в результате междисциплинарного взаимодействия.

В 1942 году Уолтер Питтс, американский логик, работавший в основном в области когнитивной психологии, познакомился со знаменитым физиологом Уорреном Маккалоком.

Маккалок приехал в Чикаго, чтобы работать в местном университете.

Питтсу негде было жить, и Маккалок предложил жить с ним.

Результатом возникших взаимоотношений стала работа «Логическое исчисление идей, относящихся к нервной деятельности».

В работе предложена модель нервной деятельности человека.

Эта модель была основана на абстракции понятия нейрона.

Математический объект, возникающий в результате этой абстракции, называется нейроном Мак-Каллоха-Питтса.

Нейрон Мак-Каллоха-Питтса представляет собой формальную модель нервной клетки, состоящей из тела и нескольких отростков, называемых нервными волокнами.

В модели Мак-Каллоха-Питтса ячейка — это ячейка, снабженная специальным числовым атрибутом, называемым порогом.

Из каждого нейрона выходит ребро, имитирующее нервное волокно и называемое аксоном.

Аксон может разветвляться, но всегда является входным сигналом для одного или нескольких других нейронов.

Таким образом, помимо исходящего волокна (аксона) нейрон имеет несколько входящих волокон (синапсов).

Некоторые входные сигналы могут быть возбуждающими, другие тормозящими.

Возбуждающие волокна обозначены правильной стрелкой, тормозные — ломаной.

Каждый нейрон генерирует сигнал на своем аксоне только в том случае, если количество возбуждающего сигнала превышает порог этого нейрона.

Аксоны обозначены сплошными исходящими стрелками.

Тело нейрона обозначено треугольником.

Таким образом, нейрон Мак-Каллоха-Питтса можно изобразить следующим образом: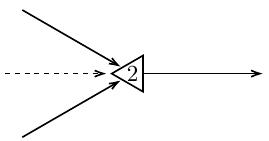

Как появились регулярные выражения?

Нейроны объединяются в сети, называемые нейронными сетями Мак-Каллоха-Питтса.

Вся сеть функционирует как конечный автомат. Для этого в сеть вводится понятие времени.

В каждый момент времени выходной сигнал определенного нейрона поступает на вход того нейрона, к которому этот нейрон подключен в качестве входа.

Таким образом, фиксируя моменты времени, мы получаем состояния нервной сети, причем переход из одного состояния в другое происходит по мере увеличения текущего момента времени.

Аксоны некоторых нейронов сети могут быть синапсами для одних и тех же нейронов, т.е.

нейроны могут образовывать «петли».

Наличие петель очень важно для нейронной сети МакКаллоха-Питтса.

Циклы позволяют запомнить сигналы, которые были поданы на вход. Если на вход нейрона был подан сигнал, то можно возбудить аксон, являющийся входом для этого же нейрона, и таким образом, с этого момента этот нейрон будет находиться в активном состоянии, самовосстанавливающемся.

захватывающе с каждым новым моментом времени.

Рассмотрим, например, нейронную сеть Мак-Каллоха-Питтса, которая является простейшим запоминающим устройством.

Собственно запоминающим устройством будет один нейрон с петлей, остальные элементы сети — «обслуживающие» элементы.

Как появились регулярные выражения?

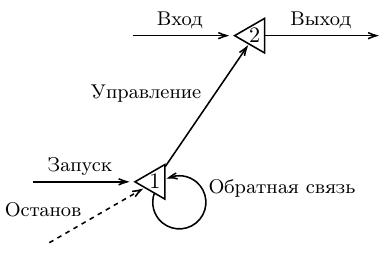
Возбуждение определенного сигнала на выходе сети будем называть событием.

Возникает вопрос: можно ли по этому событию определить ее предысторию, т.е.

последовательность сигналов, проходящих через сеть в предыдущие моменты времени, чтобы достичь входов в эту сеть? Если принять во внимание, что сети Мак-Каллоха-Питтса были изобретены для моделирования мозговой деятельности, то этот вопрос можно переформулировать так: какие внешние факторы привели к тому состоянию сознания, в котором он оказывается в данной ситуации? Оказывается, наличие петель не позволяет точно определить, когда произошло данное событие, а наличие альтернатив (входов от двух разных нейронов к данному нейрону) не позволяет точно определить, где это событие произошло.

Маккалок и Питтс считали, что это ограничение лежит в основе психологического феномена, называемого «абстракция».

Регулярные мероприятия

Американский математик Стивен Клини изучал события в сетях Маккаллоха-Питтса.

В книге «Представление событий в нейронных сетях и конечных автоматах» Клини предложила элегантный способ описания таких событий с помощью языка обычные выражения .

Можно сказать, что любую сеть Маккаллоха-Питтса можно представить в виде регулярного выражения, описывающего входы этой сети и историю входных сигналов, приведших к возбудимости одного из выходных сигналов.

Напомним, что событием в сети Мак-Каллоха-Питтса является появление сигнала на ее выходе, т.е.

на аксоне, не являющемся синапсом ни на одном нейроне сети.

Клини изучал вопрос: возбуждение каких входов (т. е.

синапсов некоторых нейронов сети, не являющихся аксонами каких-либо нейронов этой сети) в сети приводило к появлению сигнала на этом выходе? Рассмотрим в качестве примера сеть, показанную на рисунке ниже:

Как появились регулярные выражения?

Предположим, что на вход синапса подан сигнал, обозначенный символом а.

Единственный нейрон в этой сети имеет порог 2, поэтому аксон этого нейрона сработает только в том случае, если активен исходный синапс S. В этом случае активен аксон R, а также его ветвь, которая повторно входит в нейрон.

Что можно сказать в момент времени t об истории появления сигнала R на выходе? Оказывается, в момент t-1 аксон а был именно активен.

Можно также предположить, что в момент времени t-2 и ранее аксон а также мог быть возбужден.

Мы не можем точно сказать, произошло ли это на самом деле, а если и произошло, то в какой момент времени аксон а стал активным.

Поэтому мы выражаем нашу гипотезу посредством a*.

Таким образом, предпосылки возникновения события R можно описать выражением а*а.

Очевидно, что где бы в сети ни возникали петли, мы не сможем точно предсказать время появления возбуждающего сигнала на входе.

Есть и другие виды неточностей.

Рассмотрим следующую сеть: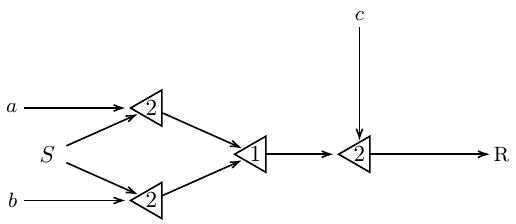

Как появились регулярные выражения?

Здесь выходной синапс R возбуждается, если аксоны с и синапс предыдущего нейрона активны.

Что мы можем сказать о том, когда этот синапс сработает? Оказывается, возбуждается только один из аксонов а или b. Обозначим этот факт выражением a|b. Таким образом, предпосылки возникновения события R можно описать как (a|b)c. В рассмотренных примерах мы получили удобный способ описания событий в сетях Маккаллоха-Питтса.

Для описания используются три оператора: *, | и оператор конкатенации.

Оказывается, эти три оператора можно использовать для описания событий в любой сети Маккалока-Питтса.

События, не описанные таким образом, не существуют в сетях Маккаллоха-Питтса.

Это является предметом доказательства т. н.

Теоремы Клини.

События, которые можно описать с помощью приведенных выше операторов, Клини назвал регулярными (в том смысле, что других событий не существует).

Регулярные события можно описать выражениями с использованием операторов *, | и конкатенация.

Такие выражения называются регулярными выражениями.

Учитывая, что каждая сеть Мак-Каллоха-Питтса является конечным автоматом, у нас есть удобный способ описания языков-автоматов с помощью регулярных выражений.

Забытое возвращается

Работа Клини была опубликована в середине 50-х годов двадцатого века.

Как это часто бывает с научными концепциями, не находящими применения, работа была забыта.

Так продолжалось бы и сейчас, но в конце 60-х годов американский программист Кен Томпсон обнаружил, что регулярные выражения удобно использовать для задания шаблонов поиска строк в длинных текстах.

Регулярное выражение преобразуется в конечный автомат, который ищет строки, соответствующие шаблону.

Для построения конечного автомата Томпсон придумал специальный алгоритм, который сейчас называется «конструкцией Томпсона».

Томпсон включил поисковую систему на основе регулярных выражений в разработанный им текстовый редактор, и с тех пор регулярные выражения стали фактическим стандартом для определения шаблонов поиска.

История понятия регулярного выражения дает хорошую возможность увидеть, как развиваются объекты человеческой мысли, путешествуя из одной области человеческой деятельности в другую.

Эти области могут находиться очень далеко друг от друга, и обмен понятиями между этими областями часто оказывается неожиданным.

Интересно, что глубокая работа Клини, в которой были представлены регулярные выражения, не сделала эту концепцию известной.

Но на самом деле именно простое утилитарное применение концепции вывело регулярные выражения на пик славы.

Теги: #регулярные выражения #нейронные сети #Алгоритмы