Java-Реализация Хешированного Двоичного Дерева

Мой друг любит говорить (не знаю, его ли это слова или он их где-то взял), что люди становятся программистами по двум причинам: если ты хочешь стать хакером или если ты хочешь писать игры.

Мой случай второй.

Меня всегда интересовала разработка игр и та часть, которая отвечает за искусственный интеллект в играх.

Я потратил много времени на изучение алгоритмов поиска пути.

Реализация следующей версии алгоритм А* в Java я столкнулся с интересной ситуацией, связанной с коллекциями TreeSet и TreeMap. Хотелось бы сразу представить два понятия, которые я буду использовать на протяжении всей статьи: поиск равенства И сравнительный поиск .

Поиск по равенству Я вызову поиск в коллекции, где для сравнения элементов используются методы равно И хэш-код .

Сравнение поиска или поиск на основе сравнения, я назову поиск элемента в коллекции, где для сравнения элементов используются методы сравнивать И по сравнению с .

Алгоритм A* использует две коллекции для хранения путевых точек: открытый список и закрытый список.

Путевая точка, грубо говоря, имеет для нас три важных атрибута: координату X, координату Y и значение метрической функции — F. Для замкнутого списка нужно выполнить всего две операции: добавление и поиск.

С открытым списком все несколько сложнее.

При открытом списке, кроме операций добавления и поиска элемента, необходимо также найти наименьшую точку по значению метрической функции.

Для закрытого списка выберите Хэшсет здесь все очевидно; он отлично подходит для добавления и поиска операций, если, конечно, вы не написали хорошую хеш-функцию.

Есть сложности с выбором коллекции для открытого списка.

Если вы выберете Хэшсет , что касается закрытого списка, то мы получим лучшую асимптотику для операций вставки, поиска и удаления — O(1), однако поиск минимума будет производиться за O(n).

При выборе Набор деревьев или ДеревоКарта у нас будет O(log(n)) для вставки и поиска, но для поиска и удаления минимума у нас будет тот же O(log(n)).

Вы можете просмотреть асимптотическое поведение различных коллекций здесь .

Еще одна важная деталь, связанная с ДеревоКарта И Набор деревьев – все операции с этими коллекциями используют сравнения.

Таким образом, если нас интересует поиск с учетом координат точек, то для поиска минимума мы используем значение метрической функции, а это приведет к тому, что операцию для точки можно не выполнить за где это значение было изменено.

Более того, при вставке новых значений мы можем получить неправильно построенное дерево: если мы сочтем точки с одинаковыми координатами равными и учтем это в компараторе, то новое значение не будет вставлено в дерево.

Имеет смысл использовать коллекцию на основе бинарного дерева, поскольку элементы в открытый список добавляются не так часто, а поиск минимального элемента по значению метрической функции осуществляется на каждой итерации алгоритма поиска.

Это связано с тем, что добавление в открытый список зависит от наличия аналогичного (по координатам) элемента в закрытом списке, который со временем разрастается и в нем появляется все больше и больше точек - чем больше точек в закрытом списке, тем меньше вероятность добавления элемента в список открытого списка.

Но мне также хотелось бы иметь преимущества коллекции Хэшсет .

Я решил обобщить проблему.

Пусть определена некая структура данных, в которой имеется набор полей.

Пусть также некоторые поля определяют отношение эквивалентности двух элементов данной структуры, а другие поля определяют отношения порядка (проще говоря, методы Equals и hashCode используют одни поля объекта, а методы Compare и CompareTo используют другие).

Задача: реализовать структуру данных, в которой операция поиска элемента на основе равенства выполняется с асимптотикой O(1), а операции вставки и удаления работают с учетом операций как сравнения, так и равенства, и построить в такой таким образом, чтобы самый маленький элемент был корнем дерева.

Поскольку для моих целей мне необходимо хранить точки в открытом списке с учетом их координат, я могу однозначно определить хеш-функцию исходя из размера карты трафика, чтобы в ней не было коллизий, поэтому я решил задать максимальное количество элементов в коллекции как константа.

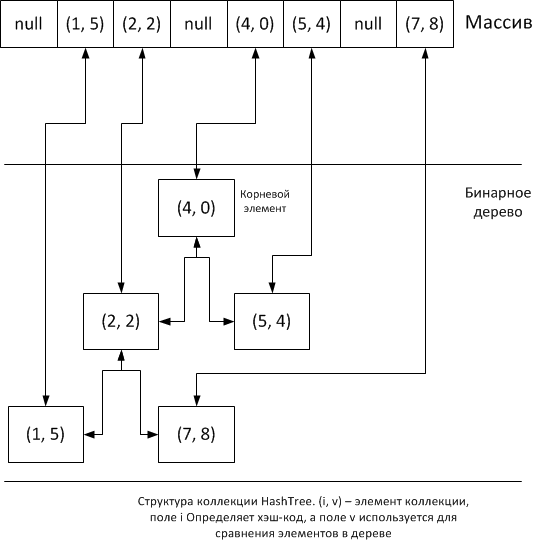
Java-реализация хешированного двоичного дерева

Идея очень проста: мы поместим элементы коллекции в массив на основе хеширования и сразу же поместим эти же элементы в бинарное дерево.

Нам нужен внутренний класс для упаковки элементов в узлы дерева:

   

 private static class Node<V extends Comparable<V>> {
 
         private Node parent;
         private Node left;
         private Node right;
         private int k = 0;
         private final V data;
 
         public Node(V data) {
             this.data = data;
             this.parent = null;
             this.left = null;
             this.right = null;
         }
 
     }

Тип V определяет элемент коллекции, он должен расширить класс Comparable, чтобы иметь возможность выполнять сравнения для построения дерева.

В классе помимо указателей на левого и правого потомка есть указатель на предка.

Это сделано для оптимизации процесса удаления элемента из дерева - имея предка удаляемого элемента, можно исключить из алгоритма удаления обход дерева начиная с корня; вы можете использовать массив элементов для поиска.

Поле имени к содержит количество узлов поддерева, если они не являются последовательными возрастающими узлами вдоль левого дочернего элемента.

Java-реализация хешированного двоичного дерева

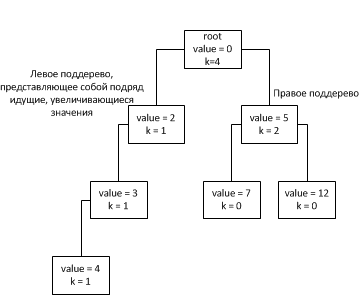
Внутри коллекции должен быть указатель на корень дерева и массив элементов коллекции, где в пустых ячейках хранится null, а в заполненных ячейках хранятся экземпляры класса.

Узел , где в поле данные будет сохранено значение добавленного элемента (точнее, значение указателя на экземпляр объекта):

public abstract class HashTree<E extends Comparable<E>> { private Node root = null; private Node[] nodes; public HashTree(int capacity) { this.nodes = new Node[capacity]; } public abstract int getElementHash(E element); … }

Как и тип V, тип Е определяет элемент коллекции.

По умолчанию коллекция пуста, поэтому указатель на корневой элемент равен нулю, а массив также заполнен значениями.

нулевой .

Абстрактный класс с абстрактным методом ПолучитьЭлементХэш , что позволяет переопределить вычисление хеш-кода.

Теперь о методах.

Метод добавитьЭлемент :

public void addElement(E element) {

Теги: #java #бинарные деревья #коллекции #Высокая производительность #java #Разработка игр