Три физики хотели рассчитать процесс изменения нейтрино.
В результате они обнаружили неожиданную связь между некоторыми из наиболее распространенных объектов математики.

Однажды в августе, утром после завтрака, математик Теренс Тао открыл электронное письмо, написанное тремя незнакомыми ему физиками.
Трио объяснило ему, что они наткнулись на простую формулу, которая, если окажется верной, опишет неожиданную связь между некоторыми из самых основных и важных объектов линейной алгебры.
Формула «выглядела слишком хорошо, чтобы быть правдой», сказал Тао, профессор и лауреат Калифорнийского университета в Лос-Анджелесе.
Медаль Филдса , один из ведущих математиков мира.
«Что-то такое короткое и простое должно было быть в учебниках уже давно», — сказал он.
«Поэтому сначала я подумал: нет, этого не может быть».
А потом он подумал еще немного.
Физики – Стивен Парк из Национальной ускорительной лаборатории.
Ферми, Синин Чжан из Чикагского университета и Питер Дентон из Брукхейвенской национальной лаборатории — получил это математическое тождество двумя месяцами ранее, пытаясь понять странное поведение элементарных частиц, называемое нейтрино .
Они это заметили» собственные векторы ", трудновычислимые величины, которые в их случае описывали, как нейтрино распространяются через материю, приравниваются к комбинации членов, известных как "собственные значения", которые гораздо легче вычислить.
Более того, они поняли, что эта связь между собственными векторами и собственными значениями - объекты, весьма распространенные в математике, физике и инженерных расчетах, изучаемые с XVIII века, - видимо, более общего порядка.
Хотя физики не могли поверить, что открыли новый факт, связанный с такой базовой математикой, они не могли найти такой связи ни в каких книгах и статьях.
Поэтому они решили рискнуть и связаться с Тао, несмотря на то, что на его сайте была просьба не беспокоить его в таких случаях.
«К нашему удивлению, он ответил через два часа и сказал, что никогда раньше не видел ничего подобного», — сказал Пак.
И кроме этого, ответ Тао содержал три независимых доказательства этого тождества.

Синин Чжан, Питер Дентон и Стивен Парк с открытой ими формулой
Полторы недели спустя физики и Тао, которого Пак называет «пожарным шлангом математики», опубликовали в Интернете работа , анонсируя новую формулу.
Эту работу сейчас оценивают специалисты журнала Communications in Mathematical Physics. В отдельном работа , опубликованную в Журнале физики высоких энергий, Дентон, Парк и Чжан используют эту формулу для упрощения уравнений, описывающих поведение нейтрино.
Эксперты говорят, что эта формула может иметь больше применений, поскольку во многих задачах требуется вычисление собственных векторов и собственных значений.
«Оно имеет самое широкое применение», — сказал Джон Биком , физик элементарных частиц из Университета Огайо.
«Кто знает, какие двери она может открыть».
Математики думают так же.
«Это одновременно удивительно и интересно», — сказал Ван Вю , математик из Йельского университета.
«Я не осознавал, что можно вычислить собственные векторы, используя только информацию о собственных значениях».
Ву и Тао доказали свою близость в 2009 году (именно поэтому Дентон, Пак и Чжан решили связаться с Тао), но новая формула не следует очевидным образом из старой.
И хотя подобная формула случайно появилась в математической статье в мае этого года, ее авторы не связали ее с собственными векторами и собственными значениями.
В некотором смысле неудивительно, что новая идея о математических объектах многовековой давности исходит от физиков.
Природа вдохновила математические исследования с тех пор, как люди начали считать на 10 пальцах.
«Чтобы математика процветала, она должна быть связана с природой», — сказал Ву.
"Другого пути нет."
Фокусы трансформации
Собственные векторы и собственные значения настолько распространены, потому что они характеризуют линейные преобразования: операции, которые растягивают, сжимают, вращают или иным образом изменяют все части одного объекта одинаково.Эти преобразования представлены прямоугольными массивами чисел, называемыми матрицами.
Одна матрица поворачивает объект на 90 градусов; другой переворачивает его вверх дном и уменьшает вдвое.

Применение этой матрицы к данному объекту отразит его относительно плоскости, а также удвоит его высоту.
Собственные векторы матрицы описывают направления, по которым объект не изменяется, кроме масштабирования.
Собственные значения матрицы описывают, насколько объект масштабируется по этим собственным векторам.
Собственный вектор А параллелен вертикальной оси.
Его собственное значение равно 2, поскольку объект удваивает свою высоту.
Собственный вектор B находится в плоскости отражения.
Его собственное значение равно 1, поскольку объект не меняется вдоль него.
Собственный вектор C перпендикулярен плоскости отражения.
Его собственное значение равно -1, что означает, что он отражается относительно плоскости.
Удаляя строки и столбцы матрицы, вы можете создавать матрицы меньшего размера.
Их собственные значения вместе с собственными значениями исходных матриц можно использовать для вычисления собственных векторов исходных матриц.
Матрицы делают это путем изменения «векторов» объектов — математических стрелок, указывающих на каждое физическое местоположение объекта.
Собственные векторы матрицы — это те векторы, которые после применения матрицы продолжают указывать в том же направлении, что и раньше.
Допустим, мы возьмем матрицу, которая поворачивает объект на 90 градусов вокруг оси x: собственные векторы направлены вдоль оси x, поскольку точки, расположенные вдоль этой оси, не вращаются, когда все остальные вращаются вокруг них.
Подобная матрица может вращать объекты вокруг оси X и сжимать их пополам.
Насколько матрица сжимает или растягивает собственные векторы объекта, описывается соответствующими собственными значениями — в данном случае 1/2 (если собственный вектор не меняется, его собственное значение равно 1).

Теренс Тао
Собственные векторы и собственные значения независимы и обычно их приходится рассчитывать отдельно, начиная со строк и столбцов самой матрицы.
Учащиеся учатся делать это для простых матриц.
Но новая формула отличается от существующих методов.
«Что интересно в этой идентичности, так это то, что вам не нужно знать ни одно из значений, содержащихся в матрице, чтобы что-либо вычислить», — сказал Тао.
Идентичность относится к Эрмитовые матрицы , осуществляющий реальные преобразования собственных векторов (в отличие от мнимых чисел), и, следовательно, применимый к ситуациям, происходящим в реальности.
Формула выражает каждый собственный вектор эрмитовой матрицы через собственные значения этой матрицы и ее «малой матрицы» — матрицы меньшего размера, которая получается удалением строк и столбцов из исходной.
Оглядываясь назад, по словам Тао, формула имеет смысл, поскольку собственные значения второстепенной матрицы кодируют скрытую в ней информацию.
Однако «я, например, лично никогда бы не подумал о таком».
Он сказал, что в математике редко встречается инструмент, не связанный с задачей.
Однако он считает, что связь между собственными векторами и собственными значениями должна быть важной.
«Это настолько прекрасно, что я уверен, что эта формула найдет применение в ближайшем будущем», — сказал он.
«На данный момент у нас есть только одно применение».
Быличастицы
И это применение связано с нейтрино: самыми странными, наименее изученными и наиболее секретными из известных фундаментальных частиц.Триллионы этих частиц проходят через человеческое тело каждую секунду, но поскольку они едва обнаруживают свое присутствие, многие их свойства остаются неизвестными.
Интересно, что теория утверждает, что именно различия в поведении нейтрино и антинейтрино могут быть причиной доминирование материи над антиматерией во Вселенной .
Если бы эти две противоположности появились после Большого взрыва в равных количествах, они бы уничтожили друг друга, и в космосе не осталось бы ничего, кроме света.
Разница между нейтрино и антинейтрино может создать существенный избыток материи.
«Если они будут вести себя по-другому, это даст нам некоторое представление о том, почему Вселенная наполнена материей», — сказала она.
Дебора Харрис , физик из Йоркского университета и лаборатории Фермилаб, работающий над нейтринным экспериментом.
ДЮНА (Глубокий подземный эксперимент с нейтрино), предназначенный для измерения таких различий.
Эксперимент, в ходе которого будут измеряться характеристики нейтрино, выпущенных из лаборатории Фермилаборатории в Иллинойсе в подземный детектор, расположенный в Южной Дакоте в 1300 км от источника, использует тот факт, что нейтрино бывают трех разных типов — электронные, мюонные и тау.
Однако каждый тип представляет собой квантовомеханическую смесь, и нейтрино колеблются, меняя свой тип по ходу движения.
По мере того, как нейтрино покидают Фермилаб, их смесь меняется, поэтому мюонное нейтрино может превратиться в электронное или тау-нейтрино.
Эти колебания описываются чрезвычайно сложной матрицей 3х3. Из собственных векторов и собственных значений физики могут вычислить выражение, описывающее вероятность того, что мюонное нейтрино превратится в электрон к моменту прибытия в Южную Дакоту.
Они также вычислили вероятность того, что мюонное нейтрино станет электронным антинейтрино.
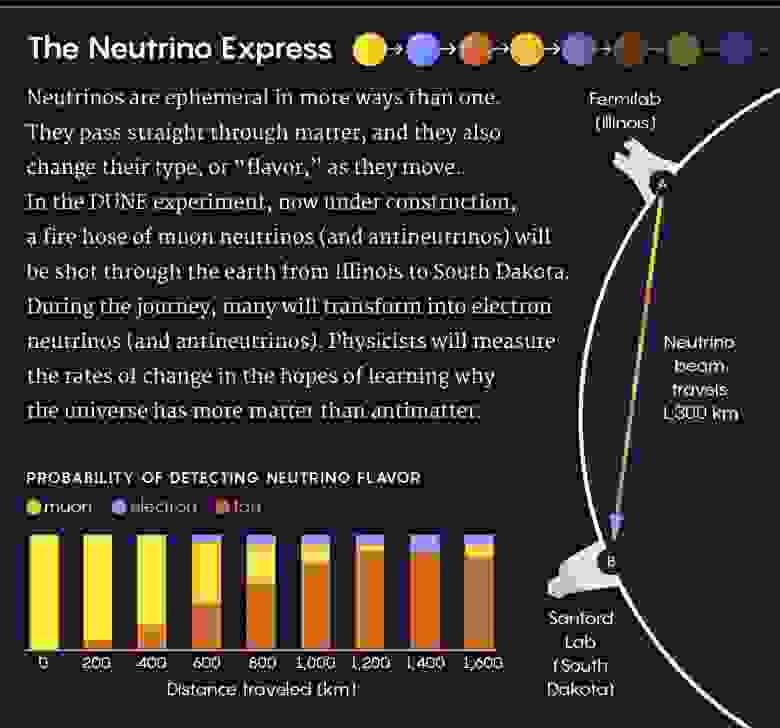
Частицы фимерных нейтрино не только проходят сквозь вещество, но и на лету меняют свой тип.
Эксперимент «ДЮНА» запустит пучок нейтрино, многие из которых изменят свой тип по пути от источника к мишени.
Именно эти изменения и будут измерять физики.
На диаграмме показана вероятность обнаружения разных типов нейтрино в зависимости от расстояния их пробега в км.
Желтый – мюон, синий – электрон, коричневый – тау.
В этих выражениях есть неизвестное: «фаза Нарушения CP ", показывая, насколько модели колебаний нейтрино и антинейтрино отличаются друг от друга.
Измеряя и сравнивая фактические коэффициенты колебаний, ученые DUNE могут вычислить это неизвестное.
Если фаза разрушения достаточно велика, это поможет объяснить, почему Вселенная заполнена с материей.
И как будто этих осложнений было недостаточно, один странный эффект, предпосылка которого была впервые обнаруженный в 1978 году физиком Линкольном Вольфенштейном, делает матрицу нейтрино еще более сложной.
Нейтрино редко взаимодействуют с материей в обычном смысле этого слова, но Вольфенштейн обнаружил, что их прохождение через материю, а не через пустое пространство, меняет способ их распространения.
Иногда нейтрино, проникая сквозь вещество, взаимодействует с электронами в атоме, существенно меняясь с ним местами: электронное нейтрино превращается в электрон и наоборот. Такие замены вводят в матрицу новый член, влияющий на электронные нейтрино, что существенно усложняет математику.
Именно этот эффект Михеев - Смирнов - Wolfenstein [который был предсказан и теоретически изучен советскими физиками Станиславом Михеевым и Алексеем Смирновым в 1985 году на основе случая Вольфенштейна нейтринных осцилляций в среде с постоянной плотностью] побудил Парка, Чжана и Дентона искать способ упростить расчеты.
Выражение для вычисления собственных значений проще, чем выражение для собственных векторов, поэтому Парк, Чжан и Дентон использовали его в качестве отправной точки.
Перед этим они разработали новый метод приближенного вычисления собственных значений.
На основании этого они заметили, что длинные выражения для собственных векторов из предыдущих работ были равны комбинациям этих собственных значений.
Объединив все это вместе, «колебания нейтрино в материи можно легко и быстро рассчитать», — сказал Чжан.
Что касается того, как именно они заметили закономерность, из которой следует формула, физики не до конца уверены.
Пак говорит, что они просто заметили отдельные закономерности и обобщили их.
Он также признается, что хорошо разгадывает загадки.
Он является соавтором еще одного важный образец , обнаруженный в 1986 году, который облегчил вычисления в физике элементарных частиц и продолжает вдохновлять на новые открытия сегодня.
И все же тот факт, что странное поведение нейтрино может привести к новым идеям, связанным с матрицей, многих шокировал.
«Люди решают задачи линейной алгебры уже очень давно», — сказал Пак.
– Я все жду, пока кто-нибудь пришлет мне электронное письмо, в котором будет написано: «Если вы посмотрите на эту малоизвестную работу Коши , то эта формула есть в примечании к третьему приложению».
Незначительная разница
На самом деле подобная формула уже была известна, но ее никто не заметил, поскольку она была замаскирована.В сентябре Тао получил еще одно неожиданное электронное письмо, на этот раз от Цзиюань Чжана, аспиранта математики Мельбурнского университета в Австралии.
Чжан отметил, что существует эквивалентная формула в работа , написанное им совместно со своим куратором Питер Форестер в мае, до появления работ Тао и трех физиков.
Чжан и Форрестер работали в области чистой математики, теории случайных матриц.
Они применили эту формулу к проблеме, связанной с проблемой, решенной Тао и его коллегами в 1999 году.
Форестер объяснил нам, что эта формула впервые появилась в другой форме в работа 2001 автор Юлия Барышникова , математик, ныне работающий в Университете Иллинойса в Урбана-Шампейн, на чьей работе основывались Форестер и Чжан.
Но эти математики описывали объекты своей идентичности не как собственные векторы, а как члены, необходимые для вычисления собственных значений некоторых второстепенных матриц, появившихся в ходе решения их задачи.
Форестер назвал формулу в своей работе и работе Чжана «идентичной» той, которую использовали Тао и трое физиков.
Тао назвал формулы «почти идентичными», относящимися друг к другу так же, как две стороны иллюзии кролика и утки.
«Некоторые люди искали кроликов, другие — только уток», — сказал он.

Дентон написал в электронном письме, что предыдущая формула была «близка к нашему результату, но не идеальна».
Он добавил, что «в свете важности собственных векторов для многих задач мы по-прежнему считаем, что наш результат достаточно отличается от других, чтобы считаться новым».
Возможно, не так уж и странно, что данная территория подверглась таким внезапным беспорядкам за одно лето после нескольких столетий.
«В математике есть много примеров одновременных открытий», — сказал Тао.
– Результаты как-то висят в воздухе.
И люди просто начинают искать их в нужных местах».
Теги: #Популярная наука #математика #физика #нейтрино #матрицы #нейтринные осцилляции #собственные значения #собственные векторы

-
Интеллектуальный Школьный Совет
19 Oct, 24


