Во всех задачах обучения искусственного интеллекта есть одно самое неприятное явление — ошибки в разметке последовательности обучения.
Эти ошибки неизбежны, так как вся разметка производится вручную, ведь если есть способ разметить реальные данные программно, то зачем нам учить кого-то еще, как это размечать, и тратить время и деньги на создание совершенно ненужного дизайна! Задача поиска и удаления фальшивых масок в большой обучающей последовательности довольно сложна.
Вы можете просмотреть их все вручную, но это не избавит вас от повторных ошибок.
Но если внимательно посмотреть на предложения в предыдущие сообщения инструментов исследования нейронных сетей, оказывается, что существует простой и эффективный способ обнаружить и извлечь все артефакты из обучающей последовательности.
А в этом посте есть конкретный пример, очевидно простой, на эллипсах и полигонах, для обычной U-сети, опять же такой простой в песочнице, но необычайно конкретный, полезный и эффективный.
Мы покажем, как простой метод выявляет и находит почти все артефакты, всю ложь обучающей последовательности.

Итак, начнем!
Как и раньше, мы будем изучать последовательности пар изображение/маска.
На картинке в разных, выбранных наугад четверти мы поместим эллипс случайной величины и четырёхугольник также произвольной величины и оба их раскрасим в один и тот же цвет, также случайно выбранный из двух из них.
Используйте второй оставшийся цвет, чтобы нарисовать фон.
Размеры как эллипса, так и четырехугольника, конечно, ограничены.
Но в этом случае мы внесем изменения в программу генерации пар и наряду с вполне правильной маской подготовим еще и неправильную, отравленную ложью - примерно в одном проценте случаев мы заменим в маске четырехугольник с эллипсом, т.е.
на ложных масках истинный объект для сегментации будем обозначать как эллипс, а не четырехугольник.
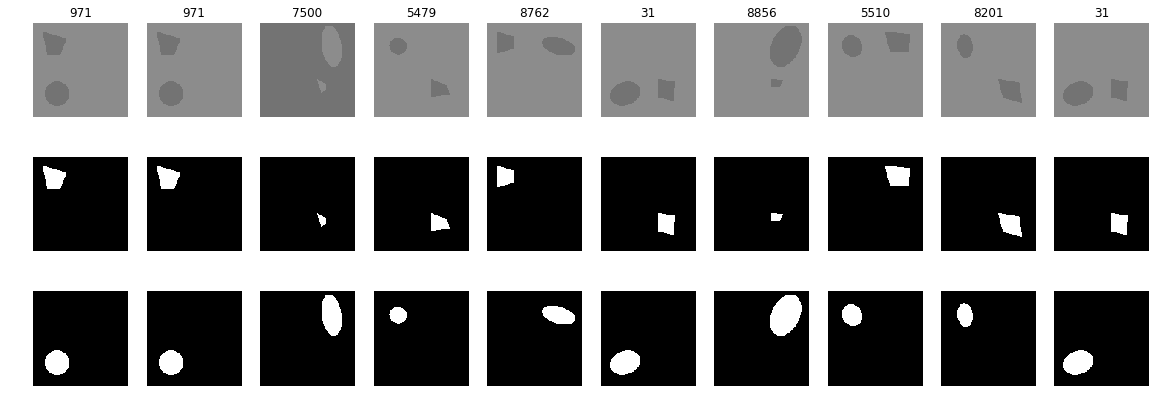
Случайные 10 примеров 
Примеров рандомных 10, но из ошибочной разметки.
Верхняя маска — истина, нижняя — ложь, а на рисунках показаны числа в обучающей последовательности.
Для сегментации мы будем использовать те же программы для расчета метрик и потерь и тот же простой U-net, но не будем использовать Dropout. Библиотеки
Метрика и функции потерьimport numpy as np import matplotlib.pyplot as plt from matplotlib.colors import NoNorm %matplotlib inline import math from tqdm import tqdm #from joblib import Parallel, delayed from skimage.draw import ellipse, polygon from keras import Model from keras.optimizers import Adam from keras.layers import Input,Conv2D,Conv2DTranspose,MaxPooling2D,concatenate from keras.layers import BatchNormalization,Activation,Add,Dropout from keras.losses import binary_crossentropy from keras import backend as K from keras.models import load_model import tensorflow as tf import keras as keras w_size = 128 train_num = 10000 radius_min = 10 radius_max = 30
def dice_coef(y_true, y_pred):
y_true_f = K.flatten(y_true)
y_pred = K.cast(y_pred, 'float32')
y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32')
intersection = y_true_f * y_pred_f
score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f))
return score
def dice_loss(y_true, y_pred):
smooth = 1.
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = y_true_f * y_pred_f
score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
return 1. - score
def bce_dice_loss(y_true, y_pred):
return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred)
def get_iou_vector(A, B):
# Numpy version
batch_size = A.shape[0]
metric = 0.0
for batch in range(batch_size):
t, p = A[batch], B[batch]
true = np.sum(t)
pred = np.sum(p)
# deal with empty mask first
if true == 0:
metric += (pred == 0)
continue
# non empty mask case. Union is never empty
# hence it is safe to divide by its number of pixels
intersection = np.sum(t * p)
union = true + pred - intersection
iou = intersection / union
# iou metrric is a stepwise approximation of the real iou over 0.5
iou = np.floor(max(0, (iou - 0.45)*20)) / 10
metric += iou
# teake the average over all images in batch
metric /= batch_size
return metric
def my_iou_metric(label, pred):
# Tensorflow version
return tf.py_func(get_iou_vector, [label, pred > 0.5], tf.float64)
from keras.utils.generic_utils import get_custom_objects
get_custom_objects().
update({'bce_dice_loss': bce_dice_loss })
get_custom_objects().
update({'dice_loss': dice_loss })
get_custom_objects().
update({'dice_coef': dice_coef })
get_custom_objects().
update({'my_iou_metric': my_iou_metric })
Обычный U-net
def build_model(input_layer, start_neurons):
# 128 -> 64
conv1 = Conv2D(start_neurons * 1, (3, 3),
activation="relu", padding="same")(input_layer)
conv1 = Conv2D(start_neurons * 1, (3, 3),
activation="relu", padding="same")(conv1)
pool1 = Conv2D(start_neurons * 1, (2, 2),
strides=(2, 2), activation="relu", padding="same")(conv1)
# pool1 = Dropout(0.25)(pool1)
# 64 -> 32
conv2 = Conv2D(start_neurons * 2, (3, 3),
activation="relu", padding="same")(pool1)
conv2 = Conv2D(start_neurons * 2, (3, 3),
activation="relu", padding="same")(conv2)
pool2 = Conv2D(start_neurons * 1, (2, 2),
strides=(2, 2), activation="relu", padding="same")(conv2)
# pool2 = Dropout(0.5)(pool2)
# 32 -> 16
conv3 = Conv2D(start_neurons * 4, (3, 3),
activation="relu", padding="same")(pool2)
conv3 = Conv2D(start_neurons * 4, (3, 3),
activation="relu", padding="same")(conv3)
pool3 = Conv2D(start_neurons * 1, (2, 2),
strides=(2, 2), activation="relu", padding="same")(conv3)
# pool3 = Dropout(0.5)(pool3)
# 16 -> 8
conv4 = Conv2D(start_neurons * 8, (3, 3),
activation="relu", padding="same")(pool3)
conv4 = Conv2D(start_neurons * 8, (3, 3),
activation="relu", padding="same")(conv4)
pool4 = Conv2D(start_neurons * 1, (2, 2),
strides=(2, 2), activation="relu", padding="same")(conv4)
# pool4 = Dropout(0.5)(pool4)
# Middle
convm = Conv2D(start_neurons * 16, (3, 3),
activation="relu", padding="same")(pool4)
convm = Conv2D(start_neurons * 16, (3, 3)
, activation="relu", padding="same")(convm)
# 8 -> 16
deconv4 = Conv2DTranspose(start_neurons * 8,
(3, 3), strides=(2, 2), padding="same")(convm)
uconv4 = concatenate([deconv4, conv4])
# uconv4 = Dropout(0.5)(uconv4)
uconv4 = Conv2D(start_neurons * 8, (3, 3)
, activation="relu", padding="same")(uconv4)
uconv4 = Conv2D(start_neurons * 8, (3, 3)
, activation="relu", padding="same")(uconv4)
# 16 -> 32
deconv3 = Conv2DTranspose(start_neurons * 4,
(3, 3), strides=(2, 2), padding="same")(uconv4)
uconv3 = concatenate([deconv3, conv3])
# uconv3 = Dropout(0.5)(uconv3)
uconv3 = Conv2D(start_neurons * 4, (3, 3)
, activation="relu", padding="same")(uconv3)
uconv3 = Conv2D(start_neurons * 4, (3, 3)
, activation="relu", padding="same")(uconv3)
# 32 -> 64
deconv2 = Conv2DTranspose(start_neurons * 2,
(3, 3), strides=(2, 2), padding="same")(uconv3)
uconv2 = concatenate([deconv2, conv2])
# uconv2 = Dropout(0.5)(uconv2)
uconv2 = Conv2D(start_neurons * 2, (3, 3)
, activation="relu", padding="same")(uconv2)
uconv2 = Conv2D(start_neurons * 2, (3, 3)
, activation="relu", padding="same")(uconv2)
# 64 -> 128
deconv1 = Conv2DTranspose(start_neurons * 1,
(3, 3), strides=(2, 2), padding="same")(uconv2)
uconv1 = concatenate([deconv1, conv1])
# uconv1 = Dropout(0.5)(uconv1)
uconv1 = Conv2D(start_neurons * 1, (3, 3)
, activation="relu", padding="same")(uconv1)
uconv1 = Conv2D(start_neurons * 1, (3, 3)
, activation="relu", padding="same")(uconv1)
# uncov1 = Dropout(0.5)(uconv1)
output_layer = Conv2D(1, (1,1), padding="same", activation="sigmoid")(uconv1)
return output_layer
input_layer = Input((w_size, w_size, 1))
output_layer = build_model(input_layer, 27)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-4), metrics=[my_iou_metric])
model.summary()Программа для генерации картинок и масок - настоящих и фейковых.
Изображение помещается в массив как первый слой, истинная маска — как второй, а ложная маска — как третий слой.
def next_pair_f(idx):
img_l = np.ones((w_size, w_size, 1), dtype='float')*0.45
img_h = np.ones((w_size, w_size, 1), dtype='float')*0.55
img = np.zeros((w_size, w_size, 3), dtype='float')
i0_qua = math.trunc(np.random.sample()*4.)
i1_qua = math.trunc(np.random.sample()*4.)
while i0_qua == i1_qua:
i1_qua = math.trunc(np.random.sample()*4.)
_qua = np.int(w_size/4)
qua = np.array([[_qua,_qua],[_qua,_qua*3],[_qua*3,_qua*3],[_qua*3,_qua]])
p = np.random.sample() - 0.5
r = qua[i0_qua,0]
c = qua[i0_qua,1]
r_radius = np.random.sample()*(radius_max-radius_min) + radius_min
c_radius = np.random.sample()*(radius_max-radius_min) + radius_min
rot = np.random.sample()*360
rr, cc = ellipse(
r, c,
r_radius, c_radius,
rotation=np.deg2rad(rot),
shape=img_l.shape
)
p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min)
p1 = qua[i1_qua,0] - (radius_max-radius_min)
p2 = qua[i1_qua,1] - (radius_max-radius_min)
p3 = np.rint(np.random.sample()*radius_min)
p4 = np.rint(np.random.sample()*radius_min)
p5 = np.rint(np.random.sample()*radius_min)
p6 = np.rint(np.random.sample()*radius_min)
p7 = np.rint(np.random.sample()*radius_min)
p8 = np.rint(np.random.sample()*radius_min)
poly = np.array((
(p1, p2),
(p1+p3, p2+p4+p0),
(p1+p5+p0, p2+p6+p0),
(p1+p7+p0, p2+p8),
(p1, p2),
))
rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape)
if p > 0:
img[:,:,:1] = img_l.copy()
img[rr, cc,:1] = img_h[rr, cc]
img[rr_p, cc_p,:1] = img_h[rr_p, cc_p]
else:
img[:,:,:1] = img_h.copy()
img[rr, cc,:1] = img_l[rr, cc]
img[rr_p, cc_p,:1] = img_l[rr_p, cc_p]
img[:,:,1] = 0.
img[:,:,1] = 0.
img[rr_p, cc_p,1] = 1.
img[:,:,2] = 0.
p_f = np.random.sample()*1000.
if p_f > 10:
img[rr_p, cc_p,2] = 1.
else:
img[rr, cc,2] = 1.
i_false[idx] = 1
return img
Программа расчета шпаргалки def make_sh(f_imgs, f_msks, val_len):
precision = 0.85
batch_size = 50
t = tqdm()
t_batch_size = 50
raw_len = val_len
id_train = 1
#id_select = 1
v_false = np.zeros((train_num), dtype='float')
while True:
if id_train == 1:
fit = model.fit(f_imgs[m2_select>0], f_msks[m2_select>0],
batch_size=batch_size,
epochs=1,
verbose=0
)
current_accu = fit.history['my_iou_metric'][0]
current_loss = fit.history['loss'][0]
if current_accu > precision:
id_train = 0
else:
t_pred = model.predict(
f_imgs[raw_len: min(raw_len+t_batch_size,f_imgs.shape[0])],
batch_size=batch_size
)
for kk in range(t_pred.shape[0]):
val_iou = get_iou_vector(
f_msks[raw_len+kk].
reshape(1,w_size,w_size,1), t_pred[kk].
reshape(1,w_size,w_size,1) > 0.5) v_false[raw_len+kk] = val_iou if val_iou < precision*0.95: new_img_test = 1 m2_select[raw_len+kk] = 1 val_len += 1 break raw_len += (kk+1) id_train = 1 t.set_description("Accuracy {0:6.4f} loss {1:6.4f} selected img {2:5d} tested img {3:5d} ".
format(current_accu, current_loss, val_len, raw_len))
t.update(1)
if raw_len >= train_num:
break
t.close()
return v_false
Базовая программа расчета.
Мы внесли небольшие изменения в ту же программу из предыдущего поста и некоторые переменные требуют пояснений и комментариев.
i_false = np.zeros((train_num), dtype='int')
Есть индикатор того, что маска ложная.
Если 1, то маска из F_msks не совпадает с маской из f_msks. Это показатель того, что мы на самом деле будем искать – ложные маски.
m2_select = np.zeros((train_num), dtype='int')
Индикатор того, что данная картинка выбрана для шпаргалки.
batch_size = 50
val_len = batch_size + 1
# i_false - false mask marked as 1
i_false = np.zeros((train_num), dtype='int')
# t_imgs, t_msks -test images and masks
_txy = [next_pair_f(idx) for idx in range(train_num)]
t_imgs = np.array(_txy)[:,:,:,:1].
reshape(-1,w_size ,w_size ,1) t_msks = np.array(_txy)[:,:,:,1].
reshape(-1,w_size ,w_size ,1) # m2_select - initial 51 pair m2_select = np.zeros((train_num), dtype='int') for k in range(val_len): m2_select[k] = 1 # i_false - false mask marked as 1 i_false = np.zeros((train_num), dtype='int') _txy = [next_pair_f(idx) for idx in range(train_num)] f_imgs = np.array(_txy)[:,:,:,:1].
reshape(-1,w_size ,w_size ,1) f_msks = np.array(_txy)[:,:,:,1].
reshape(-1,w_size ,w_size ,1) # F_msks - mask array with ~1% false mask F_msks = np.array(_txy)[:,:,:,2].
reshape(-1,w_size ,w_size ,1) fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): kk = np.random.randint(train_num) axes[0,k].
set_axis_off() axes[0,k].
imshow(f_imgs[kk].
squeeze(), cmap="gray", norm=NoNorm()) axes[1,k].
set_axis_off() axes[1,k].
imshow(f_msks[kk].
squeeze(), cmap="gray", norm=NoNorm()) plt.show(block=True) false_num = np.arange(train_num)[i_false>0] fig, axes = plt.subplots(3, 10, figsize=(20, 7)) for k in range(10): kk = np.random.randint(false_num.shape[0]) axes[0,k].
set_axis_off() axes[0,k].
set_title(false_num[kk]) axes[0,k].
imshow(f_imgs[false_num[kk]].
squeeze(), cmap="gray", norm=NoNorm()) axes[1,k].
set_axis_off() axes[1,k].
imshow(f_msks[false_num[kk]].
squeeze(), cmap="gray", norm=NoNorm()) axes[2,k].
set_axis_off() axes[2,k].
imshow(F_msks[false_num[kk]].
squeeze(), cmap="gray", norm=NoNorm())
plt.show(block=True)
Мы строим последовательности пар изображение/маска для обучения и еще одну последовательность для тестирования.
Те.
Мы проверим новую независимую последовательность из 10 000 пар.
Отображаем и визуально выборочно проверяем случайные картинки с истинными и ложными масками.
Сами картинки представлены выше.
В данном конкретном случае результатом стали 93 фальшивые маски, на которых как истинный позитив был отмечен эллипс, а не четырехугольник.
Начинаем тренировку на правильном наборе, используя в качестве маски f_msks input_layer = Input((w_size, w_size, 1))
output_layer = build_model(input_layer, 25)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-4), metrics=[my_iou_metric])
v_false = make_sh(f_imgs, f_msks, val_len)
t_pred = model.predict(t_imgs,batch_size=batch_size)
print (get_iou_vector(t_msks,t_pred.reshape(-1,w_size ,w_size ,1)))
Accuracy 0.9807 loss 0.0092 selected img 404 tested img 10000 : : 1801it [08:13, 3.65it/s]
0.9895299999999841
Шпаргалка состояла всего из 404 картинок, и на независимой тестовой последовательности мы получили приемлемую точность.
Теперь снова компилируем сеть и обучаем ее, используя ту же обучающую последовательность, но в качестве масок вводим F_msk с 1% ложных масок.
input_layer = Input((w_size, w_size, 1))
output_layer = build_model(input_layer, 25)
model = Model(input_layer, output_layer)
model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-4), metrics=[my_iou_metric])
v_false = make_sh(f_imgs, F_msks, val_len)
t_pred = model.predict(t_imgs,batch_size=batch_size)
print (get_iou_vector(t_msks,t_pred.reshape(-1,w_size ,w_size ,1)))
Accuracy 0.9821 loss 0.0324 selected img 727 tested img 10000 : : 1679it [25:44, 1.09it/s]
0.9524099999999959
Мы получили шпаргалку из 727 картинок, что существенно больше, а точность предсказания тестовой последовательности, как и в предыдущем тесте, снизилась с 0,98953 до 0,9525. Мы добавили ложь в обучающую последовательность менее чем на 1%, только 93 маски из 10 000 были ложью, но результат ухудшился на 3,7%.
И это не просто ложь, это самый настоящий обман! А шпаргалка увеличилась всего лишь с 404 до 727 картинок.
Только одно успокаивает и радует print (len(set(np.arange(train_num)[m2_select>0]).
intersection(set(np.arange(train_num)[i_false>0]))))
93
Поясню эту длинную формулу: мы берем пересечение набора картинок, выбранных для шпаргалки, с набором ложных картинок и видим, что алгоритм выбрал для шпаргалки все 93 ложные картинки.
Задача значительно упростилась; это не 10000 картинок, которые нужно просмотреть вручную, это всего 727 и вся ложь сосредоточена здесь.
Но есть еще более интересный и полезный способ.
Когда мы составляли шпаргалку, мы включали в нее только те пары картинка/маска, предсказание которых было меньше порога, а в нашем конкретном случае мы сохраняли значение точности предсказания в массиве v_false .
Давайте посмотрим на пары из обучающей последовательности, которые имеют очень маленькое значение прогноза, например меньше 0,1, и посмотрим, сколько там лжи.
print (len(set(np.arange(train_num)[v_false<0.01]).
intersection(set(np.arange(train_num)[i_false>0]))))
89
Как видите, основная часть ложных масок, 89 из 93, оказалась в этих масках.
np.arange(train_num)[v_false<0.01].
shape
(382,)
Таким образом, если мы проверим вручную только 382 маски, а это из 10 000 штук, то большая часть фальшивых масок будет нами выявлена и уничтожена без всякой жалости.
Если при принятии решения об их включении в шпаргалку можно просмотреть картинки и маски, то, начиная с определенного шага, все ложные маски, вся ложь будут определяться минимальным уровнем прогнозирования слабообученной сети и корректироваться.
маски будут иметь прогноз выше этого уровня.
Давайте подведем итоги
Если в каком-то вымышленном мире истина всегда четырехугольная, а ложь овальная, и некая неизвестная сущность решила исказить истину и назвала некоторые эллипсы истиной, а четырехугольники ложью, то, используя искусственный интеллект и естественную способность сочинять шпаргалки, местная инквизиция быстро и легко найдет и искоренит ложь и обман целиком и полностью.P.S. Способность обнаруживать овалы, треугольники и простые многоугольники — необходимое условие для создания любого ИИ, управляющего автомобилем.
Если вы не умеете искать овалы и треугольники, вы не найдете всех дорожных знаков и ваш ИИ поведет машину не в ту сторону.
Теги: #Машинное обучение #Алгоритмы #искусственный интеллект #Обработка изображений

-
Кеттелл, Джеймс Маккин
19 Oct, 24 -
Истории Разработчиков: Trekkit Traveler
19 Oct, 24


