
Привет коллеги.
В конце 1960-х годов прошлого века Ричард Фейнман читать в Калифорнийском технологическом институте курс лекций по общей физике.
Фейнман согласился провести свой курс ровно один раз.
В университете понимали, что лекции станут историческим событием, и обязались записывать все лекции и фотографировать все рисунки, которые Фейнман делал на доске.
Возможно, именно после этого в университете сохранилась привычка фотографировать все доски, к которым прикасалась рука.
Фото справа — в год смерти Фейнмана.
В левом верхнем углу написано: " То, что я не могу создать, я не понимаю «Это говорили себе не только физики, но и биологи .
В 2011, Крейг Вентер был создан первый в мире синтетический живой организм, т. е.
ДНК этого организма рукотворная.
Организм не очень большой, всего одна клетка.
Помимо всего, что необходимо для воспроизводства программы жизни, в ДНК были закодированы имена создателей, их электронные адреса и цитата Ричарда Фейнмана (правда, с ошибкой, которая, кстати, позже была исправлена).
Хотите знать, почему эта классная вещь здесь? Приглашаю вас на разрез, коллеги.
Введение
На протяжении веков люди пытались создать вещи, принцип действия которых не могу объяснить .Первой реальной моделью искусственного интеллекта, вовсе не мифической и вполне понятной как работающей, стала Персептрон Розенблатта .
А потом все начало крутиться .
Давайте более подробно рассмотрим область компьютерного зрения.
Сегодня нейронные сети отлично решают задачи классификации, сегментации и т. д., но как они это делают? Какие особенности изучает сеть и имеют ли они смысл — эти вопросы можно считать почти решенными.
Вот пример этого , как результаты этой работы позволяют нам сегодня манипулировать изображением.
Но манипулировать – это не творить, верно? Есть еще проблемы, например, в эта работа вы можете увидеть, как добавление шума к изображению заставляет топовую нейросеть совершать ошибки, хотя невооруженным глазом изменений не увидеть.
Теперь, если бы мы могли создавать изображения, то, возможно, мы могли бы поставить точку в вопросе понимания того, чему на самом деле обучается нейронная сеть и почему она делает то, а не другое.
Помните, вот как Межзвездный — последняя граница в понимании гравитационной сингулярности лежит в самой сингулярности.
Вопрос алгоритмической генерации фотореалистичных изображений не нов, но только в эпоху глубокого обучения были достигнуты значительные результаты.
Сегодня мы поговорим об одном из таких подходов, который стал одним из главных достижений последних лет в глубоком обучении.
Оригинальная статья называется «Генераторно-состязательные сети» (GAN), и, хотя устоявшегося перевода нет, мы будем называть их GAN. Мне кажется, варианты «генеративно-конкурентные сети» (GCN) или «генеративно-состязательные сети» (GCN) звучат как-то не правильно.
Для начала давайте рассмотрим таксономию генеративных моделей, основанных на максимизации правдоподобия данных (в том числе тех, которые делают это неявно; существуют и другие подходы к генерации данных, но они не пересекаются с GAN).
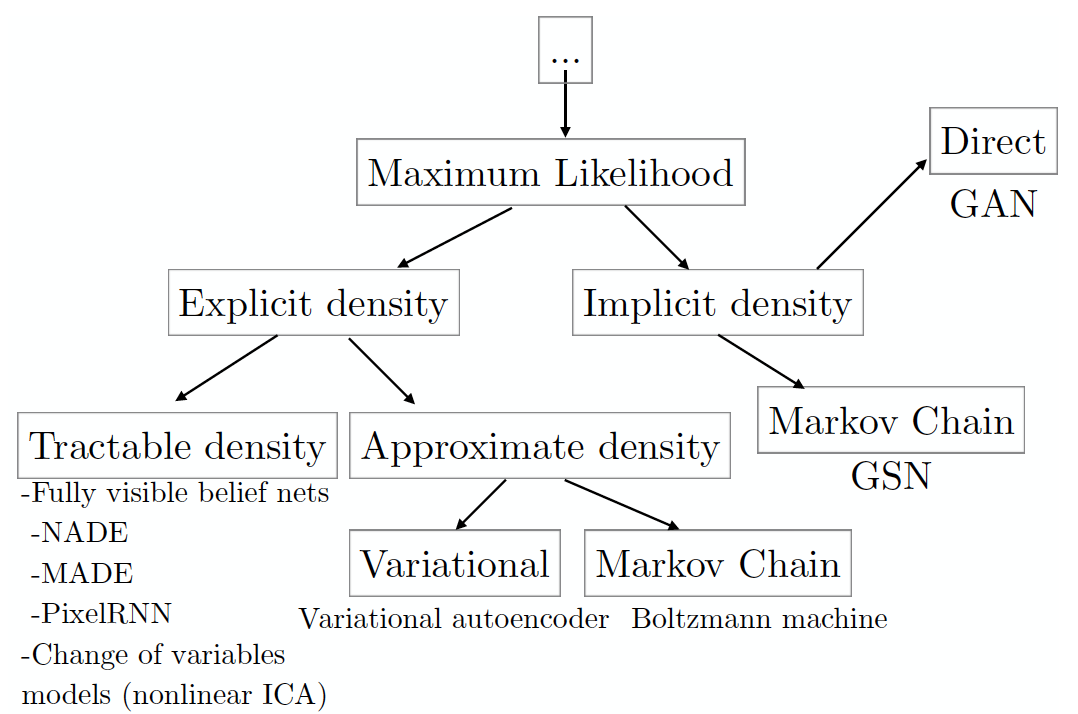
(изображение взято с статьи автор GAN, составленного на основе его семинара на конференции NIPS 2016 года; Отсюда вольный пересказ в нескольких абзацах ниже).
Давайте вспомним, что суть принцип максимального правдоподобия заключается в поиске параметров модели, которые максимизируют вероятность набора данных, состоящего из
примеры, выбранные независимо от общей совокупности:
.
Обычно для простоты расчета логарифмическое правдоподобие максимизируется:
Максимизация правдоподобия аналогична минимизации.
KL-расхождения между реальным распределением данных и модельным:
Каждый лист дерева таксономии соответствует определенной модели, имеющей ряд плюсов и минусов.
ГАНы были разработаны для смягчения недостатков других моделей, что закономерно привело к появлению новых недостатков.
Но обо всем по порядку.
Левое поддерево содержит модели с явно заданным видом функции плотности данных.
( явная плотность ).
Для таких моделей максимизация вполне очевидна; нам нужно вставить желаемую форму плотности в формулу логарифмического правдоподобия и использовать градиентный подъем, чтобы найти лучший набор параметров
.
Основным недостатком этого подхода является именно необходимость явного выражения плотности таким образом, чтобы описать все многообразие моделируемых данных, но в то же время так, чтобы полученную оптимизационную задачу можно было решить за приемлемое время.
Если вам удастся построить все таким образом, чтобы распределение удовлетворительно описывало все многообразие данных, и одна из моделей группы управляемая плотность работает в приемлемое время, то считайте, что вам повезло (пока, кстати, единственный способ оценить качество создаваемых изображений – это визуальная оценка человеком).
Если модель выдаёт изображения посредственного качества или вы состарились пока она тренировалась, то Может быть , модели, аппроксимирующие плотность, решат проблему (см.
приблизительная плотность ).
Такие модели по-прежнему должны обеспечивать явную формулу плотности распределения.
Методы, основанные на вариационной аппроксимации ( переменная ), максимизировать оценку нижнего правдоподобия
, что гарантирует получение оценки реальной вероятности, как минимум не хуже полученной.
Для многих невычислимых распределений можно найти нижние границы, которые можно вычислить за разумное время.
Основным недостатком таких моделей является то, что разрыв между нижней оценкой
и реальная достоверность может быть слишком велика.
Это приведет к тому, что модель
научусь чему-то другому, кроме реального распределения данных
.
Если вы столкнулись с этой проблемой, то есть еще последний шанс успешно аппроксимировать указанную вами плотность — Методы Монте-Карло ( Марковская цепь Монте-Карло , MCMC), то есть выборка.
Выборка является основным недостатком этого класса моделей.
Несмотря на то, что структура гарантирует, что когда-нибудь выборка сойдётся к
, этот процесс может занять неприемлемо много времени.
В отчаянии вы можете решить использовать модели с неявной функцией плотности ( Неявная плотность ) – модели, которые непосредственно не формулируют
, а только примеры примеров из него.
Здесь мы попадаем либо в условия предыдущего метода, когда для выборки необходимо использовать методы Монте-Карло со всеми вытекающими, либо можно использовать ГАН, генерирующие одну выборку за один проход (что сравнимо с одним шагом цепь Маркова).
Итак, давайте подведем итог, чем же так примечательны GAN:
- не требуют явной плотности, хотя можно быть уверенным в том, что искомая форма распределения усвоена (в этом смысле вариационные методы и ГАН имеют связь);
- нижняя оценка логарифмического правдоподобия не требуется;
- нет необходимости проводить выборку (точнее, выборка есть, но только в один прием, а не по цепочке);
- было замечено, что изображения лучше, чем у других моделей (субъективная оценка, конечно);
- От себя добавлю, что эта модель — одна из самых простых для понимания во всей описанной выше категоризации.
Начнем с самой первой статьи, в которой широкой публике были представлены GAN.
Генеративно-состязательные сети (10 июня 2014 г.
) Представим себе историю из фильм про противостояние фальшивомонетчика и полиции: один подделывает, другой ловит, ну вы поняли.
Что произойдет, если мы заменим то и другое нейронной сетью? Результатом будет ролевая игра, в которой пока будут только два актера.

г enerator — аналог фальшивомонетчика, сети, генерирующей данные (например, изображения), ее задача — иметь возможность производить изображения, максимально приближенные к целевой популяции.
Д искриминатор – аналог полицейского, а точнее, сотрудника аналитического отдела полиции по борьбе с фальшивомонетчиками; его задача — отличить оригинальную монету от подделки.
Таким образом, дискриминатор — это не что иное, как бинарный классификатор, который должен выдавать 1 для реальных изображений и 0 для поддельных.
Здесь стоит вспомнить Китайская комната : а что, если оптимальный дискриминатор не может отличить фейки от настоящих, можно ли считать, что генератор начал генерировать реальные изображения или это всё-таки качественный фейк? В целом модель выглядит так и обучается сквозным методом обратного распространения ошибки: 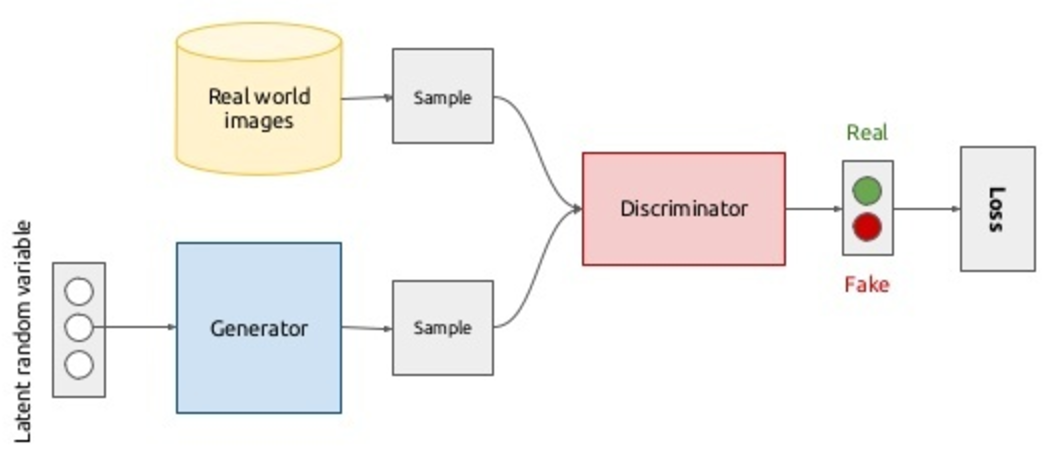
В принципе, со сценарием в верхней половине диаграммы все понятно: мы выбираем изображения из базы реальных изображений (
), мы присваиваем им метку 1 и пропускаем через дискриминатор, таким образом получаем вероятности принадлежности к классу реальных изображений.
Максимизируя логарифмическое правдоподобие дискриминатора на выборке реальных и сгенерированных (подробнее об этом позже) изображений, мы перемещаем плотность в сторону реальных изображений:
, Где
является нейронной сетью-дискриминатором, и
- его параметры.
Для обучения генератора обозначим распределение генератора как
, Где
это изображение.
Вводится некоторое априорное распределение шума.
, который отображается генератором в пространство изображения:
(
— параметры генераторной сети).
Да, вы все правильно поняли, изображения будут генерироваться из шума.
Более того, у нас есть возможность настраивать форму этого шума.
Во втором сценарии минимизированы следующие функциональные возможности:
, т. е.
мы хотим, чтобы дискриминатор как можно лучше отличал подделки от реальных изображений.
Ничто не мешает нам обновить веса генератора с помощью градиентного спуска, потому что
является дифференцируемой функцией.
Объединив все вышесказанное в одну оптимизационную задачу, получим следующее минимакс игра для двух игроков:
Вы можете заметить, что это очень похоже на начальные условия обучения с подкреплением, и будете правы.
Канал передачи информации от генератора к дискриминатору представляет собой прямой проход по сети, а обратный проход — способ передачи информации от дискриминатора к генератору.
Возникает идея обучить всю сквозную модель, просто инвертируя градиенты, исходящие от дискриминатора, что позволит дискриминатору подняться выше по ее поверхности, а генератору самостоятельно спуститься (см.
следующую часть, где авторы вводят слой обращения градиента).
Но этот подход не работает для GAN. В самом начале обучения дискриминатору очень легко отличить поддельные данные от реальных (см.
пример ниже).
Тогда для фейковых данных
, и
, что будет выражаться в затухании градиентов.
Проще говоря, никакая информация от дискриминатора не дойдет до генератора, и генератор потеряет (ничего не узнает).
Предполагая, что дискриминатор всегда будет близок к оптимальному, заменив
на
решит проблему распада, но решение минимаксной игры и новой максмаксной игры будет одинаковым.
Пример сэмплов из генератора (около 16МБ) Сравните, какие выборки производит сеть в начале обучения и на более позднем этапе.


Чтобы дискриминатор всегда был близок к оптимальному, авторы статьи предлагают следующий трюк.
На каждой итерации обучения сначала дискриминатор обучается в несколько этапов с использованием пакетов реальных и поддельных изображений с фиксированным генератором; затем делается один шаг для обучения генератора на пакете поддельных изображений с фиксированным дискриминатором.
Это позволит вам держать дискриминатор всегда около оптимального и медленно менять генератор.
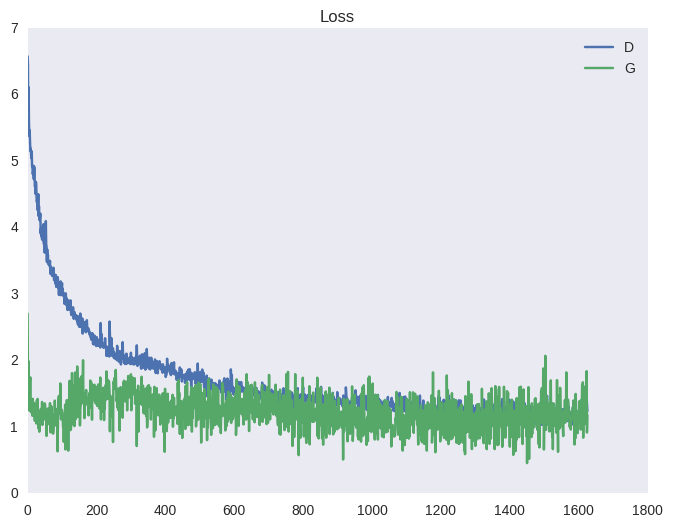
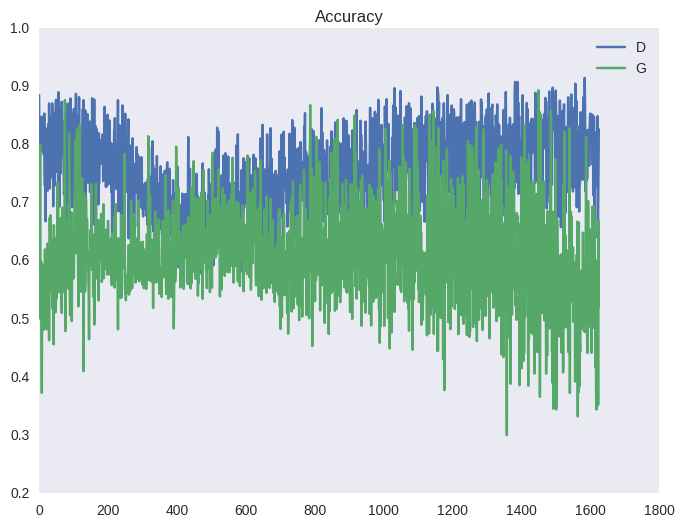
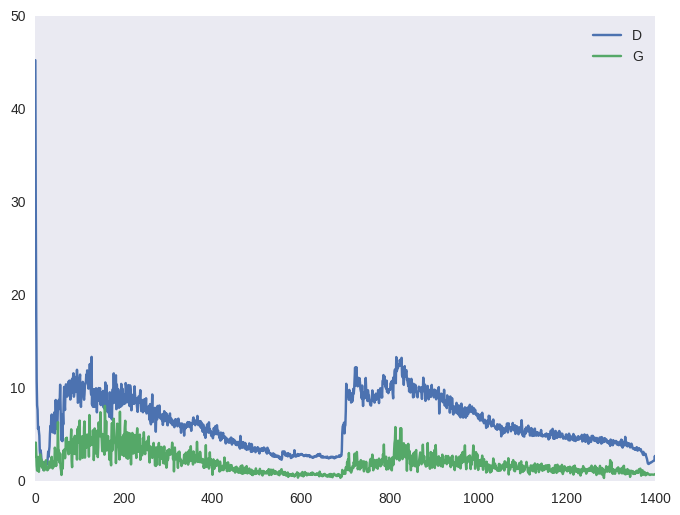
Конечным результатом является игра в перетягивание каната, которая приводит к нестабильному обучению.
Ниже приведена типичная картина для функции стоимости GAN и точности (среднее количество примеров, которые дискриминатор правильно распознает на этапе обучения и на этапе обучения генератора).
Эффект от такого перетаскивания вы можете наблюдать на графиках ниже, а также в виде ряби в примерах выше (под спойлером).
 |
 |
Давайте оценим, какие теоретические обоснования лежат в основе GAN. Во-первых, авторы доказывают, что для фиксированного генератора оптимальный дискриминатор имеет вид:
А затем доказывают теорему о существовании глобального минимума функционала порождающей функции в точке
, а также что значение функции
.
Наконец, авторы доказывают, что последовательный процесс обучения генератора и дискриминатора сходится.
Вроде бы все очень хорошо, но все эти расчеты корректны только в том случае, если мы рассматриваем все возможные функции как кандидаты на роль генератора и дискриминатора.
К сожалению, в действительности мы не можем решить задачу оптимизации в пространстве всех функций, и нам приходится ограничиться одним семейством.
В данном случае это семейство нейронных сетей, т.е.
параметрически заданных функций.
И именно это является причиной такого нестабильного поведения, изображенного на графиках выше.
При оптимизации функционала в пространстве параметров нейронных сетей (а это пространство действительных чисел очень высокой размерности) мы просто не в состоянии найти тот самый глобальный оптимум.
Почему нейронные сети? Теорема об универсальной аппроксимации доказана для нейронных сетей, и это, наверное, самый широкий класс функций, в пространстве которых мы можем искать решение.
В заключение обзора основной статьи рассмотрим идеализированную визуализацию процесса конвергенции и того, к чему она приводит: 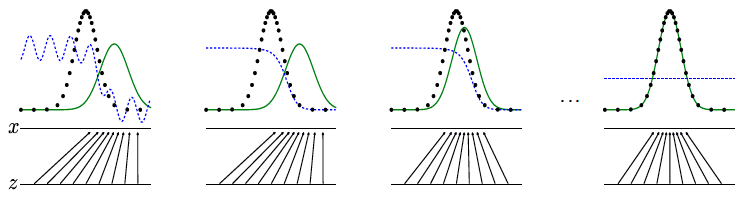
- линия черных точек — это распределение данных
, который мы хотим аппроксимировать нейронной сетью; - зеленая линия — распределение генератора
, в процессе обучения приближается к распределению данных (обучение происходит последовательно); - синяя линия — разделительная поверхность дискриминатора, который в конце обучения не может отличить примеры из реального набора данных от подделки, созданной генератором;
- стрелки показывают дисплей
, который присваивает каждое значение из распределения данных точке из предыдущего распределения.

Авторы представляют результаты четырех экспериментов.
Первые пять столбцов содержат несколько семплов из генератора, а справа — наиболее близкие реальные изображения.
Из-за использования МЛП Результаты на сложных наборах данных пока не впечатляют. Отметим четыре свойства такого обучения:
- оказывается, что изучается гладкое и компактное пространство (не путать с математическими понятиями), такое, что прототипы подобных объектов в шумовом пространстве также лежат рядом (авторы используют обычное МЛП , поэтому в одной из следующих статей мы увидим красивые визуализации, где используются свёрточные сети), и для любой точки из априорного шума есть содержательный прототип;
- генератор учится создавать близкие к реальным изображения, ни разу не видя ни одного настоящего изображения, а лишь получая от дискриминатора сигнал о том, почему обнаружена подделка, закодированный в градиентах;
- как будто они пытались избавиться MCMC , потому что это занимает много времени, но в итоге мы получили модель, которая делает выборку за один шаг, но все равно долго обучается и нестабильна (MCMC хотя бы асимптотически сходится, но здесь нет никаких гарантий в пространство параметрических функций);
- Модель красивая, но совершенно не применима для извлечения признаков из изображения, что в конечном итоге нам и нужно, поскольку мы хотим не только генерировать, но и рассчитывать прототипы реальных изображений в шумовом пространстве.
Неконтролируемая адаптация домена путем обратного распространения ошибки (26 сентября 2014 г.
) Всем казалось очевидным, что ГАНы — это весело и задорно, но пока бесполезно.
Пока человечество придумывало, как адаптировать их для извлечения признаков, «Сколково» нашло неожиданное и полезное применение GAN. Представьте себе следующую задачу: вам нужно искать одежду по реальным фотографиям в магазине типа Amazon. Для этого мы можем легко собрать размеченный набор данных, просто проанализировав Amazon. Затем присвойте каждому изображению метку в соответствии с категорией товара, обучите классификатор и используйте любое представление из сети Для поиска.
Но есть небольшая проблема: все фотографии на Amazon — это обычно студийные фотографии с белым фоном, без шума, а зачастую вообще без людей.
В то время как настоящие фотографии, используемые для поиска, сделаны на мобильный телефон и помимо естественного шума содержат еще людей и насыщенный фон.
Можно было бы, конечно, разметить датасет реальных фотографий, что стоило бы времени и денег, и совсем не ясно, поможет ли это.
Эта проблема называется Смена домена – когда обучение происходит в одной области, а применение модели – в другой.
Обычно распределение данных по доменам различно; цена маркировки данных из первого домена низкая, а цена маркировки данных из второго домена высокая; Необходимо обучить классификатор, инвариантный к предметной области, но обладающий высоким качеством классификации.
Другими словами, скрытое представление данных не должно содержать информацию о предметной области, но должно содержать информацию об объекте.
И именно здесь авторы предлагают использовать GAN. 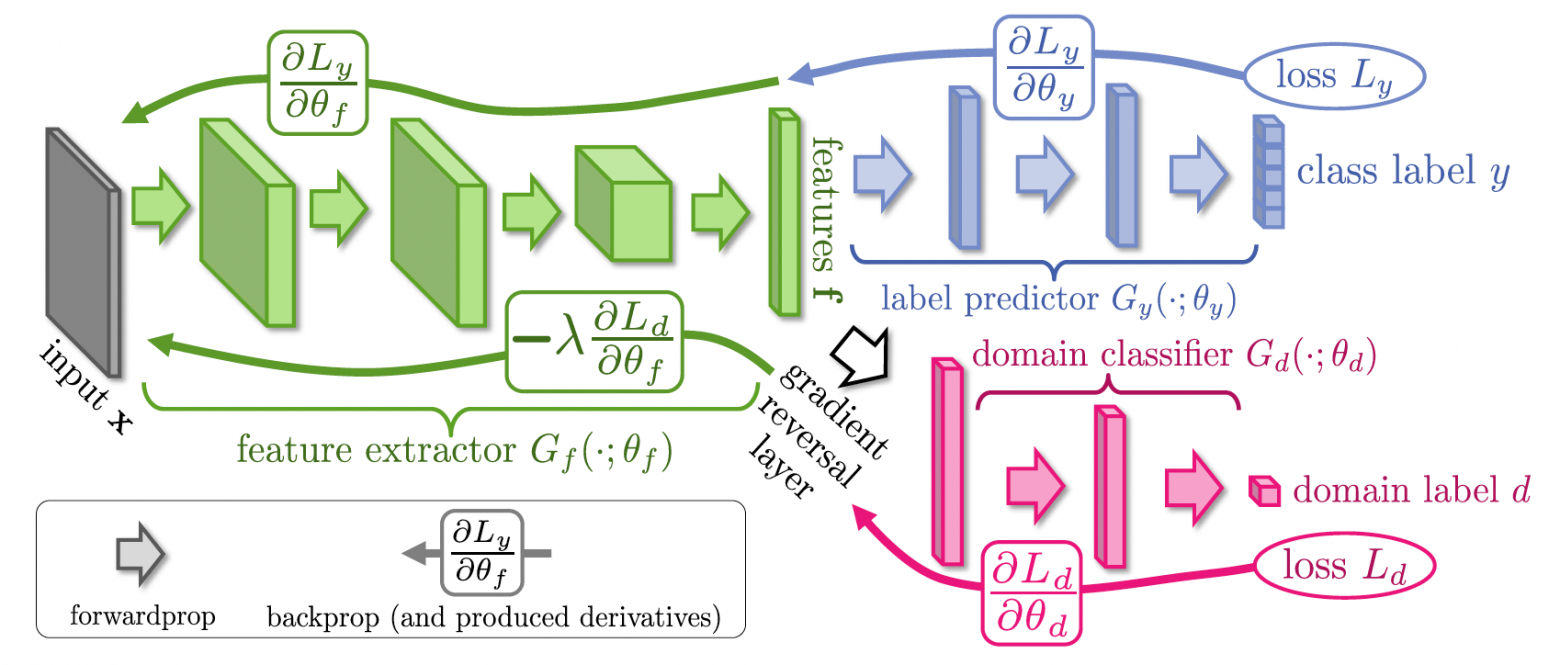
Допустим, нам нужен слой ж был инвариантен относительно предметной области, давайте прикрепим к нему еще один классификатор, как в Google Начало, версия 1 , но мы будем не минимизировать функцию стоимости, а максимизировать ее.
Таким образом мы как бы «выбьем» информацию о домене из представления.
ж , и «вбивать» информацию об объектах, поскольку обычный классификатор обучен минимизировать ошибку классификации между объектами.
Оказывается, весь этот процесс обучения можно сделать сквозным, используя слой обращения градиента, который находится между представлениями.
ж и классификатор домена.
Когда ошибка распространяется обратно через такой слой, знак градиентов инвертируется, так что часть сети до представления ж учится вычислять признаки, не содержащие информации о предметной области, поскольку именно такие признаки максимизируют ошибку классификации классификатора предметной области.
Примеры поиска фотографий из реального проекта Целевое фото: 
Топ-3 ответа: 


Условные генеративно-состязательные сети (6 ноября 2014 г.
) Спустя полгода после публикации оригинальной статьи о GAN люди еще не научились использовать их для извлечения признаков, но уже начали анализировать динамику сходимости минимаксной игры.
Было замечено, что если данные мультимодальны, решение имеет тенденцию схлопываться в одном режиме.

На этом изображении справа вы можете увидеть целевое распределение данных, а слева — процесс конвергенции обычной GAN. В результате модель выбирает понравившуюся моду и генерирует образцы только из нее.
Например, вы можете начать обучать модель генерировать рукописные цифры из набора MNIST, и она научится идеально генерировать только семерки.
Немного отличается от того, что хотелось бы получить.
В случае MNIST, когда у нас есть размеченный набор данных, авторы предлагают подавать генератору и дискриминатору не только сгенерированное изображение, но и его метку.
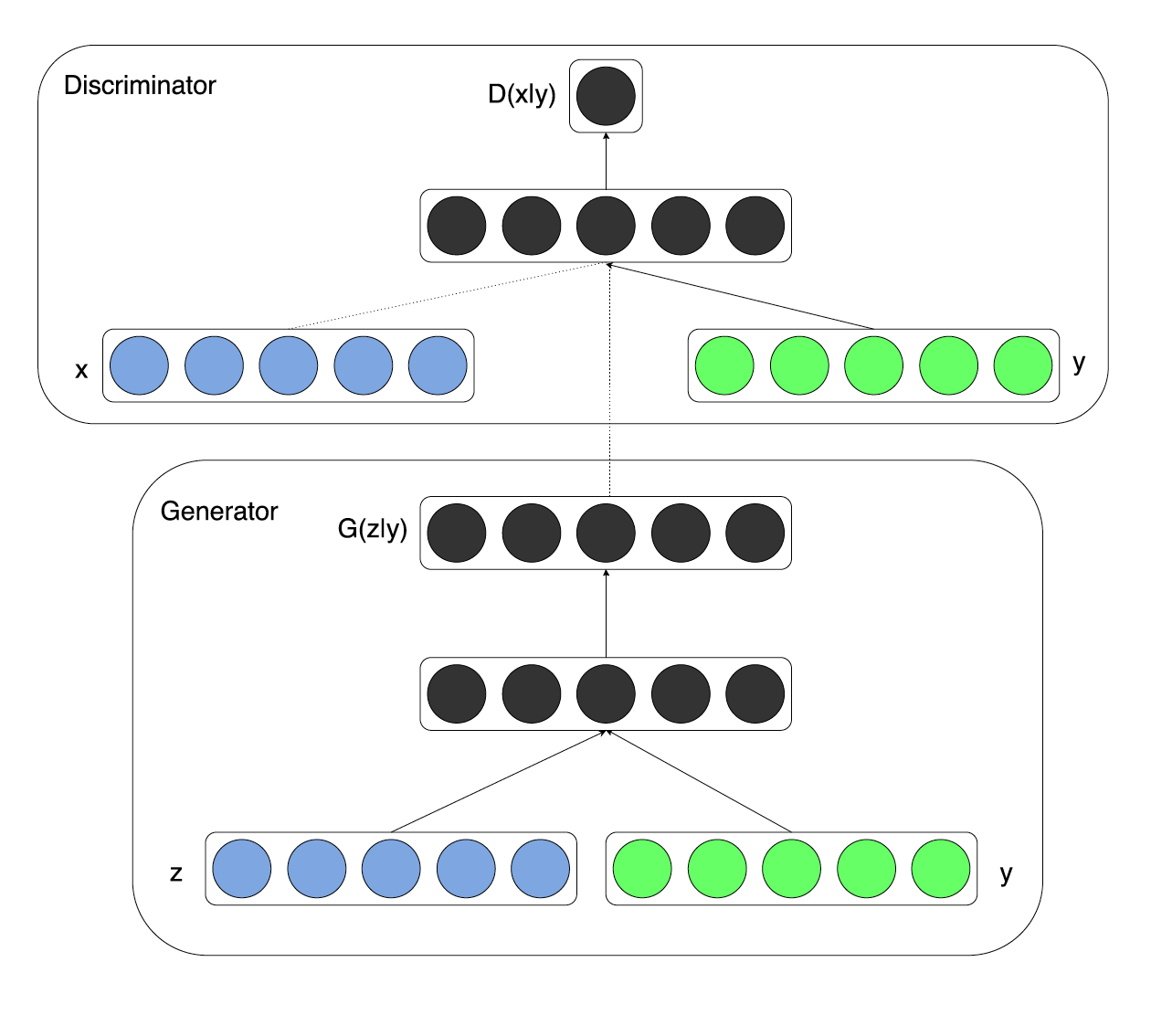
Теги: #нейронные сети #ODS #глубокое обучение #GaN #условный ган #DCGAN #cyclegan #adversarial autoencoder #aae #infogan #сеть передачи доменов #путин зебра #Алгоритмы #обработка изображений #математика #машинное обучение

-
Заключение
19 Oct, 24 -
Проектирование В Confluence
19 Oct, 24 -
Карта Посетителей Сайта
19 Oct, 24


