Примечание : этот пост является переводом статьи cmcenroe.me/2014/12/05/days-in-month-formula.html ( Часть I ), а также авторские дополнения к нему ( Часть II ).
Материал не следует воспринимать всерьез, а скорее как умственное упражнение, требующее не более чем школьных знаний арифметики и не имеющее практического применения.
Приятного чтения всем! Часть I
Введение
Недавно, после очередной бессонной ночи, я задумался о методах запоминания количества дней в каждом месяце года.Для этого есть считалка, а также способ считать на костяшках пальцев, но ни то, ни другое меня не устроило.
Я задавался вопросом, может ли существовать какая-то математическая формула для решения такой проблемы, и, не найдя ее в ходе быстрого изучения, я поставил перед собой задачу создать ее.
Другими словами, формализуя, необходимо найти функцию ж , такой, что значение е(х) за каждый месяц Икс , представленный числом от 1 до 12, соответствует количеству дней в этом месяце.
Таблица значений аргументов и функций 1 : Икс 1 2 3 4 5 6 7 8 9 10 11 12 е(х) 31 28 31 30 31 30 31 31 30 31 30 31 Если у вас возникло желание попробовать это самостоятельно, прежде чем читать мое решение, сейчас самое время.
Если вы предпочитаете сразу увидеть готовый ответ, то загляните под спойлер.
Отвечать 
Ниже приведены мои шаги по поиску решения.
Математический аппарат
Во-первых, давайте кратко освежим в памяти два важнейших оператора при решении этой задачи: целочисленное деление и остаток от деления.Целочисленное деление Это оператор, используемый во многих языках программирования для деления двух целых чисел и удаления дробной части из частного.
Я изобразю его таким 
.
Например: 
Оставшаяся часть дивизии Это оператор, который находит остаток от деления.
Многие языки программирования используют символ % , я буду использовать конструкции типа 
, Например: 
Обратите внимание, что остальная часть деления имеет равный приоритет с делением.
Основы
Итак, воспользуемся нашим математическим аппаратом для получения основной формулы.
2 Обычный месяц состоит из 30 или 31 дня, поэтому мы можем использовать 
чтобы получить поочередно 1 или 0, а затем просто добавить к этому числу константу: 
Получаем таблицу с правильными значениями, выделенными жирным шрифтом: Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х)
31
30
31
30
31
30
31
30
31
30
31
30
Неплохое начало! Уже есть правильные значения для января и месяцев с марта по июль включительно.
Февраль – случай особый, и им мы займемся чуть позже.
После июля для остальных месяцев порядок получения 0 и 1 следует поменять местами.
Для этого мы можем добавить 1 к делимому: 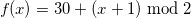
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х)
30
31
30
31
30
31
30
31
30
31
30
31
Значения за август-декабрь теперь верны, но, как и ожидалось, значения за другие месяцы неверны.
Давайте посмотрим, как можно объединить эти формулы.
Наложение маски
Для этого требуется кусочная функция, но — поскольку мне это показалось скучным — я подумал о другом решении, используя одну часть функции на одном интервале, другую — на другом.Я считаю, что проще всего было бы найти выражение, равное 1 в одной области применения и 0 в остальных.
Метод, при котором путем умножения аргумента на выражение мы исключаем его из формулы за пределами ее области действия, я назвал «наложением маски», поскольку такое поведение похоже на своеобразную битовую маску.
Чтобы применить этот метод, в последней части нашей функции нам нужно найти выражение, равное 1, когда 
, и — поскольку значения аргументов всегда меньше 16 — для этого отлично подойдет целочисленное деление на 8. Икс
1
2
3
4
5
6
7
8
9
10
11
12
⌊ Икс ⁄ 8 ⌋
0
0
0
0
0
0
0
1
1
1
1
1
Теперь с этой маской, используя в дивиденде 
выражение 
вместо 1 мы можем изменить порядок, в котором формула выдает 0 и 1: 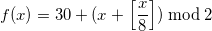
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х)
31
30
31
30
31
30
31
31
30
31
30
31
Эврика! Все верно, кроме февраля.
Сюрприз Сюрприз.
февраль
В любом месяце 30 или 31 день, кроме февраля с его 28 (високосные годы выходят за рамки данной задачи).
3 На данный момент по нашей формуле оно имеет 30 дней, поэтому было бы неплохо вычесть выражение, равное 2, когда 
.
Лучшее, что я мог придумать, это 
, который применяет маску ко всем месяцам после февраля: Икс
1
2
3
4
5
6
7
8
9
10
11
12
2 мод Икс
0
0
2
2
2
2
2
2
2
2
2
2
Изменив базовую константу на 28 и прибавив к оставшимся месяцам 2, получим формулу: 
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х)
29
28
31
30
31
30
31
31
30
31
30
31
К сожалению, январь теперь на 2 дня короче.
Но, к счастью, очень легко получить выражение, применимое только к первому месяцу: это округленная обратная величина 
число.
Умножив его на 2, получим окончательную формулу: 
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х)
31
28
31
30
31
30
31
31
30
31
30
31
Послесловие
Вот она — формула для получения количества дней в любом месяце года с помощью простой арифметики.
В следующий раз, когда вы вспомните, сколько дней в сентябре, просто сделайте 
с помощью этой однострочной функции JavaScript:
Часть IIfunction f(x) { return 28 + (x + Math.floor(x/8)) % 2 + 2 % x + 2 * Math.floor(1/x); }
Введение
В первой части была получена короткая и даже несколько изящная формула, основными преимуществами которой являются простота математического аппарата, отсутствие ветвей и условных выражений, лаконичность.К недостаткам - помимо того, что вы не будете использовать его в своем проекте - можно отнести отсутствие проверки на високосные и невисокосные годы.
Поэтому я поставил перед собой задачу создать функцию ж , такой, что значение е(х, у) за каждый месяц Икс , представленный числом от 1 до 12 и годом й , больше 0, соответствует количеству дней в месяце.
Икс в год й .
Для нетерпеливых под спойлером есть готовый ответ, а остальных прошу подписаться на меня.
Отвечать 
Остальная часть дивизии: мод И ⌊⌋
Для наглядности условимся, что в некоторых формулах оператор деления с остатком заменен на нижние скобки там, где мне это показалось необходимым: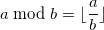
Високосный год
В високосный год вводится дополнительный календарный день: 29 февраля.Как известно, високосным годом называется год, который делится на 4 и не делится на 100 или делится на 400. Запишем выражение, идентичное этому утверждению.
: 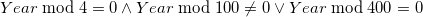
Чтобы преобразовать это выражение в алгебраическое, нужно применить выражение к результату 
инъекции типа: 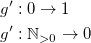
Что позволит получить 1 при делении без остатка и 0 при делении с остатком, чтобы использовать его в формуле определения количества дней в месяце.
Как функция г' вы можете использовать 1 минус остаток деления 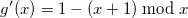
Для 
: Икс
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
г'(х)
Бесконечность
1
0
0
0
0
0
0
0
0
0
0
0
0
0
Легко видеть, что увеличив делимое и делитель на 1, мы получим правильную формулу 
в 
: Икс
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
г'(х)
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Итак, выражение 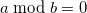
давайте напишем это как: 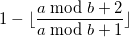
И выражение 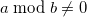
давайте напишем это как: 
Используя этот подход, мы получаем следующую функцию г(у) , значение которого будет равно 1, если год високосный, или 0 в противном случае: 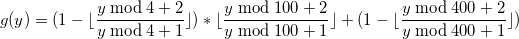
й
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
г(у)
0
0
1
0
0
0
1
0
0
0
1
й
2000
2100
2200
2300
2400
2500
2600
2700
2800
2900
3000
г(у)
1
0
0
0
1
0
0
0
1
0
0
Високосные годы выделены жирным шрифтом.
Напомню, что в рамках принятого соглашения оператор получения остатка от деления можно изобразить как мод , и ⌊⌋.
Наложение маски
В формуле
Часть

это поправка, добавляющая 2 дня к январю.
Если мы удалим множитель 2 и заменим 1 на 2 в числителе, то эта формула добавит 2 дня к январю и 1 день к февралю, что дает нам ключ к добавлению дня в високосный год. Для наглядности мы используем промежуточное значение в формуле г(у) и в качестве й Мы используем 2000 (високосный) и 2001 (невисокосный) годы: 
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х, 2000)
31
29
31
30
31
30
31
31
30
31
30
31
е(х, 2001)
30
28
31
30
31
30
31
31
30
31
30
30
Значения для всех месяцев, кроме января невисокосного года, верны.
Чтобы исправить это досадное недоразумение, прибавим к январю 1 день по уже известной нам формуле.

: 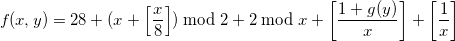
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х, 2000)
32
29
31
30
31
30
31
31
30
31
30
31
е(х, 2001)
31
28
31
30
31
30
31
31
30
31
30
30
Теперь нам нужно отнять 1 день от января в случае високосного года, для чего нам поможет знание того, что для любого Икс 
, А 
.
Тогда формула примет вид: 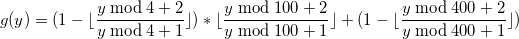
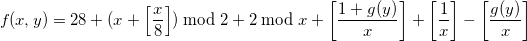
Или: 
Икс
1
2
3
4
5
6
7
8
9
10
11
12
е(х, 2000)
31
29
31
30
31
30
31
31
30
31
30
31
е(х, 2001)
31
28
31
30
31
30
31
31
30
31
30
30
Заключение
В результате была получена гораздо более громоздкая, но более универсальная формула, по которой можно также получить количество дней в месяце определенного года: function f(x, y) { return 28 + ((x + Math.floor(x / 8)) % 2) + 2 % x + Math.floor((1 + (1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1))) / x) + Math.floor(1/x) - Math.floor(((1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1)))/x); }Пример на С# ideone.com/fANutz .
1 .
Я не умею пользоваться такой мнемотехникой, поэтому посмотрел табличку в Интернете.
2 .
«Основы» или «Правило со многими исключениями», как и большинство правил.
3 .
Первоначально в римском календаре февраль был последним месяцем в году, поэтому логично, что он короче всех остальных.
Также есть логика в добавлении или удалении дня в конце года, поэтому его длина является переменной.
Обновление.
1: Альтернативный перевод первой части в Сообщество ВКонтакте .
Обновление.
2: Спасибо за комментарий кексмен Исправлена ошибка в формуле определения високосных годов ( г(у) ) и окончательная формула была исправлена.
Теги: #занимательная математика #теги никто не читает #юмор #математика

-
Проектирование В Confluence
19 Oct, 24 -
Fc-Trackbar 0.4.1 - Новое Начало
19 Oct, 24 -
Ты Веришь В Бога?
19 Oct, 24


