Язык 4DL был изобретен в 2001 году Клиффом Л.
Биффлом.
Как он сам объяснил, он придумал это, во-первых, потому, что до этого не было языков с четырехмерными программами, а во-вторых, потому что четырехмерное пространство довольно сложно понять, и необходимо дать людям возможность возможность тренировать свой мозг.
Русская Википедия относит этот язык к семейству «грибовидных».
Это языки, произошедшие от языка Бефунге , программы в которых написаны в виде символов на прямоугольной решетке и могут выполняться в любом направлении.
В 4DL для представления программы используется четырехмерная решетка и имеется соответственно 8 направлений ее выполнения.
Программа 4DL может выглядеть, например, так:
__ __ __ __ NЭта программа написана не на «базовом» языке, а на его расширении, но об этом позже.
Помимо того, что 4DL является грибовидным языком, он также является стековым языком.
Единственный объект данных, с которым может работать программа, — это стек целых чисел.
В него помещаются цифры, введенные символы, а из него берутся символы для печати.
программы 4DL
Вот как выглядит авторская система команд:| Икс | Поверните указатель команды в направлении X+.
|
| Икс | Поверните указатель команды в направлении X. |
| Да | Поверните указатель команды в направлении Y+.
|
| й | Поверните указатель команды в направлении Y. |
| З | Поверните указатель команды в направлении Z+.
|
| я | Поверните указатель команды в направлении Z. |
| Т | Поверните указатель команды в направлении T+.
|
| т | Поверните указатель команды в направлении T- |
| п | Положите в стек символ из соседней ячейки со стороны X+.
|
| п | Положите в стек символ из соседней ячейки на стороне X. |
| Б | Положите в стек символ из соседней ячейки со стороны Y+.
|
| б | Положите в стек символ из соседней ячейки со стороны Y. |
| Д | Положите в стек символ из соседней ячейки со стороны Z+.
|
| д | Положите в стек символ из соседней ячейки на стороне Z. |
| вопрос | Положите в стек символ из соседней ячейки со стороны Т+.
|
| д | Положите в стек символ из соседней ячейки на стороне Т.
|
| + | Возьмите сумму двух чисел сверху стека, положите результат в стек |
| — | Возьмите разницу двух чисел сверху стека, положите результат в стек |
| , | Введите символ с клавиатуры и поместите его в стек |
| .
|
Извлеките символ из верхней части стека и отобразите его на экране.
|
| # | Перейти на следующую ячейку программы |
| ? | Удалить число с вершины стека и, если оно ненулевое, то перепрыгнуть через следующую ячейку программы |
| 0 | Поместите число 0 в стек |
| 2 | Поместите копию числа из стека в стек |
| % | Завершить выполнение программы |
К сожалению, ни на что заметно более серьёзное язык с такими командами не способен (если не увеличивать размер программы во много раз), поэтому для начала я решил добавить в него ещё пару команд:
| \ | Поменяйте местами содержимое двух ячеек вверху стека.
|
| ^ | Удалить число из вершины стека и ничего с ним не делать (эквивалентно 2-+ или ЭXX - в случае движения вправо) |
Например, вот как выглядит программа, которая печатает сумму чисел из входной строки:
__ __ __ __ N N xНесколько слов о написании программы (это моя фантазия — автор никак не описал синтаксис ввода).
Пространство, в котором находится программа, разделено на двумерные слои, в которых координаты Z и T постоянны.
Символы каждого слоя записываются в виде прямоугольной таблицы, начиная с угла X=Y=0. Если это символ ASCII-7 (код от 33 до 126), он записывается явно.
Если нет, записывается его двузначный шестнадцатеричный код. Пробел может быть представлен как 20 или как двойное подчеркивание.
Символы пишутся через любое количество пробелов, строка с ними начинается с пробела.
Прямоугольники объединяются в двумерную таблицу.
По горизонтали располагаются слои с одинаковым значением T (последовательно: Z=0, Z=1, .
), по вертикали располагаются столбцы с одинаковым значением Z. Длины строк в слоях, количество строк в слое, количество слоев в строке таблицы могут варьироваться — недостающие ячейки будут заполнены символами с кодом 0. Слои в строке таблицы разделяются символами || а сами строки — это строки, начинающиеся с минуса.
По умолчанию выполнение начинается с ячейки (0,0,0,0) в направлении X+.
Начальную точку можно переопределить, вставив в программу строку > x,y,z,t (числа x,y,z и t десятичные).
Траектория выполнения приведенной выше программы в 4-мерном пространстве выглядит примерно так: 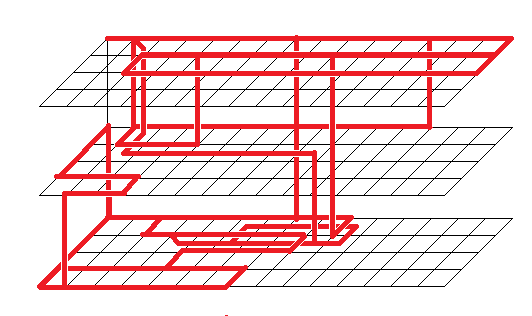
Помимо ячеек, через которые проходит красная линия, есть еще ряд ячеек с данными, но я решил их не показывать.
Тьюринг завершен или нет?
Быстро становится ясно, что мощь языка 4DL полностью определяется мощностью лежащего в его основе механизма стека.Итак, если разрядность числа в стеке ограничена, то можно реализовать те и только те алгоритмы, которые реализованы на конечных автоматах со стековой памятью.
Если стек может вмещать числа произвольной длины и у нас есть операция замены двух ячеек наверху стека, язык становится полным по Тьюрингу, но реализация на нем машины Тьюринга будет слишком медленной (одна операция займет около не менее 2^2^N шагов, где N — объем используемой памяти).
Если размер числа в стеке ограничен, но есть операция чтения и изменения ячеек глубоко в стеке (смещение сверху тоже берется из стека), то мы получаем почти язык ТП - доступный Память прямого доступа будет ограничена.
В любом случае четырехмерность программы почти не используется, и любую программу 4DL можно встроить в двумерное пространство.
При этом оставьте строку Y=0 для исполняемого кода, Y=1 для данных, а остальную часть плоскости используйте для реализации команд перехода.
Этот вариант кажется неинтересным.
С той же проблемой ограничения мощности столкнулись авторы языка Befunge. Для ее решения они добавили в язык механизм модификации ячеек памяти (что правильно), но сделали это за счет разрешения доступа к ячейкам — как на чтение, так и на запись — по явным координатам.
Мне это показалось слишком серьезным решением.
4DL+ и машина Тьюринга
Более умеренный вариант предложил автор одной из реализаций языка 4DL Бернхард Штокнер.В «расширенная» система команд для его реализации он предлагает, среди прочего, следующие команды:
| Н | Поместите символ из стопки в соседнюю ячейку на стороне X+.
|
| н | Поместите символ из стека в соседнюю ячейку на стороне X. |
| Ф | Поместите символ из стека в соседнюю ячейку на стороне Y+.
|
| ж | Поместите символ из стопки в соседнюю ячейку на стороне Y. |
| г | Поместите символ из стека в соседнюю ячейку на стороне Z+.
|
| г | Поместите символ из стека в соседнюю ячейку на стороне Z. |
| ЧАС | Поместите символ из стека в соседнюю ячейку на стороне T+.
|
| час | Поместите символ из стопки в соседнюю ячейку на стороне T. |
Чтобы доказать это, пойдём по самому простому пути — реализуем машину Тьюринга :) Наша основная проблема в том, что мы можем читать и изменять содержимое только ячеек памяти, соседних с текущей точкой выполнения программы.
Машина Тьюринга требует бесконечной или, по крайней мере, полубесконечной ленты, а это означает, что для связи с удаленными ячейками программа должна быть самомодифицирующейся.
Первой идеей было реализовать ленту в виде «небоскреба», в котором каждый этаж мог поддерживать команды «прочитать ячейку ленты», «изменить содержимое ячейки», «переместить вверх» и «переместиться вниз».
, а когда достигнет самого верха, запустить «строительную» платформу», растущую в параллельном слое реальности, для возведения нового этажа.
Проблема оказалась разрешимой, но довольно быстро был обнаружен гораздо более простой путь.
Оказывается, если взять строку программы, например, в направлении X+, заполнить левую часть пробелами и поместить куда-нибудь команду «N» (взять символ из стека и записать его в ячейку на правильно), затем положить в стек определенные последовательности команд и данных, и отправить программе на выполнение этой строки, тогда программа сможет сделать то, что вам нужно, и вернуться обратно.
Например, последовательность [N,x,x,N] превратит строку
__ __ __ N n n xв соответствии
021 120 020 110 011 110 121 020 021 120 111 110 010 120 121 121 120 011 000И если после этого отправить в эту строку последовательность [n,n,n,N,n], то вы получите строку
X , B / \ B + 2 B - < ? T B - T
y __ 10 __ __ 7 __ __ A __ __ __ __ 07 __ __
------------------------------------------------------------------
__ Y __ __ __ __ __ __ __ __ .
__ x __ __ x || __ __ __ __ __ __ __ __ __ __ 20 __ __ __ __ __
t X __ __ __ q + 2 q - < ? Z q - Z || z __ __ __ __ __ __ __ __ .
b .
x __ __ x
— крайняя левая команда «N» переместится на одну клетку влево.
Аналогично в два действия можно выполнить команды «переместить вправо», «записать символ в соседнюю строку» и «прочитать символ из соседней строки».
Удобнее всего работать с ячейкой, расположенной на две позиции правее ячейки, в которой находится команда «N».
Программа реализации машины Тьюринга будет состоять из трех частей.
Уровень T=0 будет использоваться для связи между программой и лентой.
Программа будет расположена в области T> 0, Z=0 и будет представлять собой конечный автомат (с памятью), преобразующий текущий символ на ленте в пару (новый символ, направление сдвига).
Поместим ленту на прямую Y=Z=T=1, и программа управления займет область T> 0, Z=1. Интерфейс ленты дополняет программный интерфейс: попарно (символ, направление сдвига) меняет содержимое ленты, перемещает каретку и возвращает новый символ, на который указывает каретка.
Назначение коммуникационного уровня — передача управления с программы на ленту и обратно, а также отладка печати.
Кроме того, этот слой осуществляет запуск программы (стоимость реализации: чтобы начать выполнение, необходимо явно запихнуть в стек содержимое ячейки, на которую указывает каретка).
Текущее состояние программы сохраняется с помощью модификации кода.
Для выполнения обработки управление передается в точку (2,3,0,1) в направлении Т+ и идет по прямой, заполненной командами «Т», за исключением одной ячейки, соответствующей текущему состоянию.
В этой ячейке содержится команда «x» (идти налево).
Программа «выходит на нужном этаже», меняет команду «х» на «Т», затем анализирует символ наверху стека, кладет в стек нужное направление движения и новый символ, после чего использует боковые пути для достижения «этажа», соответствующего новому состоянию, команда «x» помещается в ячейку (2,3,0,T) и переходит в плоскость Z=T=0, куда она перенаправляется для управления лента.
Собственно, это все.
Вот пример программы, реализующей удвоение числа, записанного на ленте.
В программе 7 состояний, число на ленте теперь 2 (две единицы).
Программа 0 X , D - 2 ? T D - 2 ? T D - Y || __ z __ 0D __ __ __ __ 13 __ __ __ __ 10
__ __ Y D T ? 2 - D T ? 2 - D , x || __ __ __ 10 __ __ __ __ 13 __ __ __ __ 0D
__ __ X - \ 2 2 + 2 + + 2 + + __ y
-------------------
T t __ __ __ __ __ ^ __ __ __ __ x || __ t
+ y + ^ x __ __ __ __ ^ || __ y __ __ .
B .
B x D || 01 __ __ __ __ 0A __ 0D y \ + x __ X __ y ------------------- Y 0 x \ 0 ^ , x + x || __ __ __ __ __ Y __ __ .
x
\ __ y Z ? 2 \ - x y || __ __ __ X + X 2 ? t y
D __ __ __ X + D \ y || 0A __ __ __ __ __ 3A
X \ 2 ? y D - Y || __ __ __ __ __ 01
y t ? 2 - D \ x || __ __ __ __ __ 01
Если вы запустите эту программу, она напечатает B __ Y || T X 2 Y
01 __ __ || __ __ __ P 0
__ __ __ || y \ .
+ b 2 x __ __ T .
B x || __ __ 0 X .
z __ Z __ __ __ __ || X 2 b + .
\ y
--------------------------------------------------------------------------------
__ __ __ __ __ 02 01 __ __ __ __ || Y t X # ? __ # \ __ __ N __ __ __
__ T __ __ X b b __ __ __ Y || __ __ T __ __ __ __ __ __ __ FF 00 01 01 00
X b F ? y B B Y __ __ __ || N __ p
y __ x x __ 02 00 T __ Y T || __ __ y
t __ f b __ __ __ __ __ x __ || __ __ T
|| N __ p
|| __ __ y __ __ __ __ __ __ __ __ x
|| X Q Q Q Q Q Q Q Q Q Q y
--------------------------------------------------------------------------------
__ __ __ __ __ 02 00 __ __ __ __ || __ __ t __ __ __ __ __ __ __ __ x
__ T __ __ X b b __ Y __ __ || __ __ X B B B B B B B B y
X b F ? y B B Y __ __ __ || __ __ __ 01 # # F x x N N
y __ T x __ 02 01 Y T __ __ || __ __ __
t __ f b __ __ __ x __ __ __ || __ __ 2
|| __ __ __
|| __ __ __
|| __ 00 01 # # B x x N 01 N
--------------------------------------------------------------------------------
__ __ __ __ __ 01 01 __ __ __ __ ||
__ T __ __ X b b Y __ __ __ ||
X b F ? y B B __ Y __ __ ||
y __ T x __ 02 01 T Y __ __ || __ __ __
t __ f b __ __ __ __ x __ __ || __ __ ?
--------------------------------------------------------------------------------
__ __ __ __ __ 01 00 __ __ __ __ ||
__ T __ __ X b b __ Y __ __ ||
X b F ? y B B Y __ __ __ ||
y __ T x __ 01 01 Y T __ __ || __ __ t __ x
t __ f b __ __ __ x __ __ __ || __ __ X ^ y
--------------------------------------------------------------------------------
__ __ __ __ __ 02 01 __ __ __ __ ||
__ T __ __ X b b __ __ Y __ ||
X b F ? y B B __ Y __ __ ||
y __ T x __ 01 01 __ Y t __ || __ __ __
t __ f b __ __ __ __ x __ __ || __ __ P 01
--------------------------------------------------------------------------------
__ __ __ __ __ 01 00 __ __ __ __ ||
__ T __ __ X b b Y __ __ __ ||
X b F ? y B B __ __ __ Y ||
y __ T x __ 02 01 T __ __ Y || __ __ __
t __ f b __ __ __ __ __ __ x || __ __ -
--------------------------------------------------------------------------------
__ __ __ __ __ __ __ __ __ __ __ ||
__ T __ __ % __ __ __ __ __ __ ||
X b F ? y B B Y __ __ __ ||
y __ T x __ 00 00 Y __ __ __ || __ __ __
t __ f b __ __ __ x __ __ __ || __ __ ?
--------------------------------------------------------------------------------
||
||
|| __ __ __ __ N 01 x x N
|| __ __ t __ b b b b b x
|| __ __ X B B B B B B y
|| __ __ __ n N n n 01 n
--------------------------------------------------------------------------------
||
||
|| __ __ __ __ N 01 N x x n
|| __ __ t __ b b b b b b x
|| __ __ X B B B B B B B y
|| __ __ __ N N N __ 01 n n
Каждая тройка символов — это новый символ, который нужно оставить на ленте (0 или 1), направление, в котором нужно двигаться (0 — на место, 1 — влево, 2 — вправо) и символ, оказавшийся под новое положение каретки.
Вы можете проверить, что программа все сделала правильно, и результатом стала цифра 4. Приложив некоторые усилия, эту реализацию можно адаптировать и к 2D. А вот в 4 измерениях работать несколько приятнее — свободы гораздо больше.
Что дальше?
Можно немного расширить язык — добавить команды умножения, деления с остатком и помещения числа 256 в стек (для более удобного разделения числа на байты для записи в память).Правда, с отрицательными числами будут проблемы.
Вместо 256 можно добавить команды «отделить младший байт» ([x] => [x&0xff,x> > 8]) и «приклеить младший байт» ([x,y] => [x+(y<<8)]).
But this will only make the language more convenient without changing its essence. It is more interesting to see what is superfluous in the language, and how best to use multidimensional memory. Например:
- можно ли удалить стек и оставить только 8- или 32-битный аккумулятор?
- что, если после этого мы добавим fork (каждый процесс со своим аккумулятором)?
- А что, если вместо батарей реализовать параллельный уровень данных, чтобы в каждой ячейке была одна команда и один байт данных?
- .
и заставить все ячейки работать параллельно и одновременно в каждом такте?
- Это уже оказались схемы из Майнкрафта или еще нет? А если нет, то я выпью еще.
Оба диалекта BrainFuck. Но в одном каретка бродит по многомерной памяти, и программа выглядит как линия на БФ, а в другом наоборот — программа многомерная, но память линейная.
Отличие от 4DL в том, что в обоих случаях управление и работа с памятью разделены.
Ссылки.
Страница 4DL на Esolang Страница блога автора Сайт с переводчиком Бефунге и его диалекты Brainfuck с многомерной памятью Brainfuck с многомерной программой Теги: #многомерный массив #языки программирования #эзотерические языки #Ненормальное программирование

-
Мультфильм «Вверх» Воплощен В Реальность
19 Oct, 24 -
Yiiconf 2017, Москва, 16 Июня
19 Oct, 24 -
Дайджест Игровой Индустрии: Март
19 Oct, 24 -
Https Приходит На Geektimes/Habrahabr?
19 Oct, 24


