Динамическое Программирование. Классические Задачи

Привет, Хабрахабр.

Сейчас я работаю над учебником по олимпиадному программированию, один из параграфов которого посвящен динамическому программированию.

Ниже приведен отрывок из этого абзаца.

Стараясь максимально просто объяснить эту тему, я постарался сопровождать сложные моменты иллюстрациями.

Мне интересно ваше мнение о том, насколько понятен этот материал.

Также буду рад получить совет, какие еще задачи стоит включить в этот раздел.

Во многих олимпиадных задачах по программированию решение с помощью рекурсии или перебора требует выполнения очень большого количества операций.

Попытка решить подобные задачи, например, методом перебора, приводит к превышению времени выполнения.

Однако среди задач перебора и некоторых других можно выделить класс задач, обладающих одним хорошим свойством: наличием решений некоторых подзадач (например, для меньшего числа н ), можно найти решение исходной задачи практически без поиска.

Такие задачи решаются методом динамического программирования, а под самим динамическим программированием мы подразумеваем сведение задачи к подзадачам.

Последовательности

Классическая проблема последовательности заключается в следующем.

Последовательность Фибоначчи Ф _н определяется формулами: Ф ₁ = 1, Ф ₂ = 1, Ф_н = Ф _{н – 1} + Ф _{н – 2} в н > 1. Нужно найти Ф _н по номеру н .

Одним из решений, которое может показаться логичным и эффективным, является решение с использованием рекурсии:

 
 int F(int n) {
  if (n < 2) return 1;
  else return F(n - 1) + F(n - 2);
 }

Используя такую функцию, мы решим задачу «с конца» — сократим шаг за шагом н пока не достигнем известных значений.

Но как видите, такая, казалось бы, простая программа уже есть.

н =40 работает заметно долго.

Это связано с тем, что одни и те же промежуточные данные вычисляются несколько раз — количество операций растет с той же скоростью, с которой растут числа Фибоначчи — в геометрической прогрессии.

Один из выходов из этой ситуации — сохранить уже найденные промежуточные результаты с целью их повторного использования:

 
 int F(int n) {
  if (A[n] != -1) return A[n];
  if (n < 2) return 1;
  else {
   A[n] = F(n - 1) + F(n - 2);
   return A[n];
  }
 }

Данное решение является правильным и эффективным.

Но для этой проблемы применимо и более простое решение:

 
 F[0] = 1;
 F[1] = 1;
 for (i = 2; i < n; i++) F[i] = F[i - 1] + F[i - 2];

Это решение можно назвать решением «с начала» — сначала заполняем известные значения, затем находим первое неизвестное значение ( Ф ₃ ), затем следующий и т. д., пока не доберемся до нужного.

Это именно то решение, которое является классическим для динамического программирования: мы сначала решили все подзадачи (нашли все Ф _я Для я < н ), то, зная решения подзадач, мы нашли ответ ( Ф _н = Ф _{н – 1} + Ф _{н – 2} , Ф _{н – 1} И Ф _{н – 2} уже найдены).

Одномерное динамическое программирование

Чтобы лучше понять суть динамического программирования, сначала мы более формально определим понятия задачи и подзадачи.

Пусть первоначальная задача состоит в том, чтобы найти определенное число Т с исходными данными н ₁ , н ₂ , .

, н _к .

То есть мы можем говорить о функции Т ( н ₁ , н ₂ , .

, н _к ), значение которого и есть нужный нам ответ. Тогда будем рассматривать задачи как подзадачи Т ( я ₁ , я ₂ , .

, я _к ) в я ₁ < н ₁ , я ₂ < н ₂ , .

, я _к < н _к .

Далее мы поговорим об одномерном, двумерном и многомерном динамическом программировании с к = 1, к = 2, к > 2 соответственно.

Следующая одномерная задача динамического программирования встречается в различных вариантах.

Задание 1. Подсчитайте количество последовательностей нулей и единиц длины н , в котором не встречаются две последовательные единицы.

В н < 32 a complete search will take several seconds, and with н = 64 полный перебор невозможен в принципе.

Для решения задачи методом динамического программирования сведем исходную задачу к подзадачам.

В н = 1, н = 2 ответ очевиден.

Предположим, что мы уже нашли К _{н – 1} , К _{н – 2} — количество таких последовательностей длины н – 1 и н – 2. Посмотрим, какой может быть длина последовательности н .

Если его последний символ равен 0, то первый н – 1 — любая правильная последовательность длин н – 1 (неважно, заканчивается он нулем или единицей – за ним следует 0).

Есть только такие последовательности К _{н – 1} .

Если последний символ равен 1, то предпоследний символ должен быть равен 0 (иначе будет две единицы подряд), а первый н – 2 символа – любая допустимая последовательность длины н – 2, число таких последовательностей равно К _{н – 2} .

Динамическое программирование.

Классические задачи

Таким образом, К ₁ = 2, К ₂ = 3, К _н = К _{н – 1} + К _{н – 2} в н > 2. То есть эта задача фактически сводится к нахождению чисел Фибоначчи.

2D-динамическое программирование

Классической задачей двумерного динамического программирования является задача о маршрутах на прямоугольном поле.

В разных постановках нужно посчитать количество маршрутов или найти маршрут, лучший в каком-то смысле.

Вот пара формулировок таких задач: Задача 2. Учитывая прямоугольное поле размером н * м клетки.

Вы можете сделать шаги на одну клетку вправо или вниз.

Посчитайте, сколькими способами можно добраться из левой верхней клетки в правую нижнюю.

Задача 3. Учитывая прямоугольное поле размером н * м клетки.

Вы можете делать шаги на одну клетку вправо, вниз или по диагонали вправо и вниз.

Каждая ячейка содержит натуральное число.

Вам нужно добраться из верхней левой ячейки в правую нижнюю.

Вес маршрута рассчитывается как сумма чисел из всех посещенных ячеек.

Необходимо найти маршрут с минимальным весом.

Характерной особенностью всех подобных задач является то, что каждый отдельный маршрут не может проходить через одну и ту же ячейку два и более раз.

Рассмотрим задачу 2 более подробно.

В некоторую ячейку с координатами ( я , дж ) может прийти только сверху или слева, то есть из ячеек с координатами ( я – 1, дж ) И ( я , дж – 1):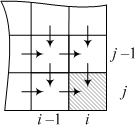

Динамическое программирование.

Классические задачи

Таким образом, для клетки ( я , дж ) количество маршрутов A[i][j] будет равно A[i – 1][j] + A[i][j – 1], то есть задача сводится к двум подзадачам.

Эта реализация использует два параметра: я И дж - следовательно, применительно к этой задаче мы говорим о двумерном динамическом программировании.

Теперь мы можем последовательно пройтись по строкам (или столбцам) массива А, находя количество маршрутов для текущей ячейки по приведенной выше формуле.

Сначала вы должны поместить число 1 в A[0][0].

В задаче 3 в ячейке с координатами ( я , дж ) мы можем получить из ячеек с координатами ( я – 1, к), ( я , дж – 1) и ( я – 1, дж - 1).

Предположим, что для каждой из этих трёх ячеек мы уже нашли маршрут минимального веса, а сами веса разместили в W[i – 1][j], W[i][j – 1], W[i – 1][j – 1].

Чтобы найти минимальный вес для ( я , дж ), необходимо выбрать минимум из весов W[i – 1][j], W[i][j – 1], W[i – 1][j – 1] и прибавить к нему число, записанное в текущая ячейка: W[i][j] = min(W[i–1][j], W[i][j – 1], W[i – 1][j – 1]) + A[i][j] ; Эта задача усложняется тем, что необходимо найти не только минимальный вес, но и сам маршрут. Поэтому в другом массиве мы для каждой ячейки дополнительно запишем, с какой стороны нам нужно в нее войти.

На следующем рисунке показан пример исходных данных и один из шагов алгоритма.

Динамическое программирование.

Классические задачи

К каждой из уже пройденных ячеек ведет ровно одна стрелка.

Эта стрелка показывает, с какой стороны нужно подойти к этой ячейке, чтобы получить минимальный вес, записанный в ячейке.

После прохождения всего массива вам нужно будет проследить сам маршрут от последней ячейки, следуя по стрелкам в обратном направлении.

Проблемы с последовательностью

Рассмотрим проблему возрастающей подпоследовательности.

Задача 4. Дана последовательность целых чисел.

Необходимо найти ее самую длинную строго возрастающую подпоследовательность.

Начнем решать задачу с начала – будем искать ответ, начиная с первых членов этой последовательности.

Для каждого номера я мы будем искать наибольшую возрастающую подпоследовательность, заканчивающуюся элементом в позиции я .

Пусть исходная последовательность хранится в массиве A. В массиве L будем записывать длины максимальных подпоследовательностей, заканчивающихся текущим элементом.

Найдем все L[i] для 1 <= я <= к – 1. Теперь мы можем найти L[k] следующим образом.

Просматриваем все элементы A[i] на предмет 1 <= я < к – 1. Если А[я] < A[k], then к Элемент-й может стать продолжением подпоследовательности, заканчивающейся элементом A[i].

Длина результирующей подпоследовательности будет на 1 больше, чем L[i].

Чтобы найти L[k], нужно пройти все я от 1 до k – 1: L[k] = max(L[i]) + 1, где максимум берется по всем я такой, что A[i] < A[k] and 1 <= я < к .

Здесь максимум пустого множества будет считаться равным 0. В этом случае текущий элемент станет единственным в выбранной последовательности, а не будет продолжением одного из предыдущих.

После заполнения массива L длина наибольшей возрастающей подпоследовательности будет равна максимальному элементу L. Для восстановления самой подпоследовательности можно также сохранить номер предыдущего выбранного элемента для каждого элемента, например, в массиве N. Рассмотрим решение этой задачи на примере последовательности 2, 8, 5, 9, 12, 6. Поскольку нет элемента раньше 2, максимальная подпоследовательность содержит только один элемент — L[1] = 1, и при этом перед ним нет элемента - N[1] = 0. Далее, 2 < 8, so 8 can be a continuation of the sequence with the previous element. Then L[2] = 2, N[2] = 1.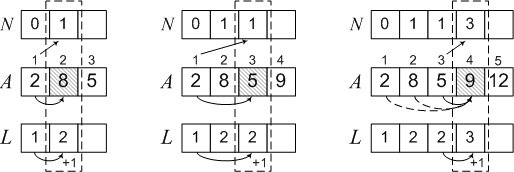

Динамическое программирование.

Классические задачи

Единственный элемент, меньший, чем A[3] = 5, — это A[1] = 2, поэтому 5 может стать продолжением только одной подпоследовательности — той, которая содержит 2. Тогда L[3] = L[1] + 1 = 2, N[3] = 1, так как 2 находится на позиции номер 1. Аналогично выполняем еще три шага алгоритма и получаем окончательный результат.

Динамическое программирование.

Классические задачи

Теперь выбираем максимальный элемент в массиве L и из массива N восстанавливаем саму подпоследовательность 2, 5, 9, 12. Другая классическая задача динамического программирования — проблема палиндрома.

Задача 5. Дана строка заглавных букв латинского алфавита.

Вам нужно найти длину наибольшего палиндрома, который можно получить, вычеркнув несколько букв из заданной строки.

Обозначим эту строку через S, а ее символы через S[i], 1 <= я <= н .

Мы рассмотрим возможные подстроки этой строки с я й дж символ, мы обозначаем их С ( я , дж ).

Длины максимальных палиндромов для подстрок запишем в квадратный массив L: L[i][j] — длина максимального палиндрома, который можно получить из подстроки С ( я , дж ).

Начнем решение задачи с простейших подстрок.

Для одной строки символов (то есть подстроки вида С ( я , я )) ответ очевиден - ничего зачеркивать не надо, такая строка и будет палиндромом.

Для двухсимвольной строки С ( я , я +1) возможны два варианта: если символы равны, то перед нами палиндром, ничего зачеркивать не надо.

Если символы не равны, то вычеркните любой.

Давайте теперь дадим подстроку С ( я , дж ).

Если первый (S[i]) и последний (S[j]) символы подстроки не совпадают, то один из них необходимо удалить.

Тогда у нас остается подстрока С ( я , дж – 1) или С ( я + 1, дж ) — то есть сводим задачу к подзадаче: L[i][j] = max(L[i][j – 1], L[i + 1][j]).

Если первый и последний символы равны, то можно оставить оба, но нам нужно знать решение задачи.

С ( я + 1, дж – 1): L[i][j] = L[i + 1][j – 1] + 2. Давайте рассмотрим решение на примере строки ABACCBA. Первым делом заполняем диагональ массива единицами, они будут соответствовать подстрокам С ( я , я ) от одного персонажа.

Затем мы начинаем рассматривать подстроки длины два.

Во всех подстроках, кроме С (4, 5) символы разные, поэтому в соответствующих ячейках пишем 1, а в L[4][5] — 2. Получается, что мы будем заполнять массив по диагонали, начиная с главной диагонали, ведущей из левого верхнего угла в правый нижний.

Для подстрок длиной 3 получаются следующие значения: в подстроке ABA первая и последняя буквы равны, поэтому L[1][3] = L[2][2] + 2. В остальных подстроках первая и последняя буквы различны.

БАК: L[2][4] = max(L[2][3], L[3][4]) = 1. АСС: L[3][5] = max(L[3][4], L[4][5]) = 2. CCB: L[4][6] = max(L[4][5], L[5][6]) = 2. CBA: L[5][7] = max(L[5][6], L[6][7]) = 1. Продолжая дальнейшие аналогичные рассуждения, заполняем все клетки под диагональю и в ячейке L[1][7] = 6 получаем ответ.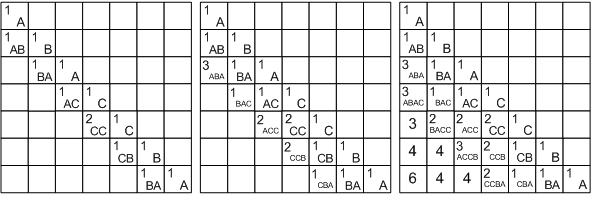

Динамическое программирование.

Классические задачи

Если в задаче необходимо вывести не длину, а сам палиндром, то помимо массива длин необходимо построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован (для наглядности на рисунке вместо числовых значений, кодирующих переходы, нарисованы соответствующие стрелки).