Всем привет! Недавно я открыл для себя язык Rust. Своими первыми впечатлениями он поделился в предыдущая статья .
Теперь я решил копнуть немного глубже, для этого мне нужно что-то посерьезнее списка.
Мой выбор пал на дерево Меркла.
В этой статье я хочу:
- расскажите нам об этой структуре данных
- посмотрите, что уже есть в Rust
- предложите свою реализацию
- сравнить производительность
В чем проблема
Дерево Меркла было изобретено еще в 1979 году, но свою популярность оно приобрело благодаря блокчейну.Цепочка блоков в сети очень велика (у биткоина она составляет более 200 ГБ), и не все узлы могут ее загрузить.
Например, телефоны или кассовые аппараты.
Однако им необходимо знать о том, что конкретная транзакция включена в блок.
Для этого был придуман протокол SPV – упрощенная проверка платежей .
Как работает дерево?
Это бинарное дерево, листьями которого являются хеши любых объектов.Для построения следующего уровня хеши соседних листьев берутся попарно, конкатенируются и вычисляется хеш результата конкатенации, что проиллюстрировано на картинке в заголовке.
Таким образом, корень дерева представляет собой хеш всех листьев.
Если вы удалите или добавите элемент, корень изменится.
Как работает дерево
Имея дерево Меркла, можно построить доказательство включения транзакции в блок как путь от хеша транзакции до корня.Например, нас интересует транзакция Tx2, доказательством для нее будет (Hash3, Hash01).
Этот механизм используется в SPV. Клиент загружает только заголовок блока с его хешем.
Имея интересующую транзакцию, он запрашивает подтверждение у узла, содержащего всю цепочку.
Затем он делает проверку, для Tx2 это будет:
Полученный результат сравнивается с корнем заголовка блока.hash(Hash01, hash(Hash2, Hash3)) = Root Hash
Такой подход делает невозможным фальсификацию доказательства, поскольку в этом случае результат проверки не будет соответствовать содержимому заголовка.
Какие реализации уже существуют? Rust — молодой язык, но на нем уже написано множество реализаций дерева Меркла.
Судя по Github, на данный момент их 56, что больше, чем в C и C++ вместе взятых.
Хотя Go их выдерживает с помощью 80 реализаций.
SpinResearch/merkle.rs
Для сравнения я выбрал эту реализацию, исходя из количества звезд в репозитории.Это дерево строится самым очевидным образом, т. е.
представляет собой граф объектов.
Как я уже отмечал, этот подход не совсем дружелюбен к Rust. Например, невозможно сделать двустороннюю связь от детей к родителям.
Построение доказательства происходит посредством поиска в глубину.
Если лист с нужным хешем найден, то результатом будет путь к нему.
Что можно улучшить
Мне не хотелось делать простую (n+1)-ю реализацию, поэтому я задумался об оптимизации.Мой код векторное дерево Меркла расположен Гитхаб .
Хранилище данных
Первое, что приходит на ум — перенести дерево в массив.Это решение будет намного лучше с точки зрения локальности данных: больше попаданий в кэш и лучшая предварительная загрузка.
Обход объектов, разбросанных по памяти, занимает больше времени.
Удобен тот факт, что все хеши имеют одинаковую длину, потому что.
рассчитываются по одному алгоритму.
Дерево Меркла в массиве будет выглядеть так: 
Доказательство
При инициализации дерева вы можете создать HashMap с индексами всех листьев.Таким образом, когда листа нет, не нужно обходить все дерево, а если есть, то можно сразу подойти к нему и подняться до корня, строя доказательство.
В своей реализации я сделал HashMap необязательным.
Конкатенация и хеширование
Казалось бы, что здесь можно улучшить? Все уже понятно — берем два хеша, склеиваем их и вычисляем новый хеш.Но дело в том, что эта функция некоммутативна, т.е.
hash(H0, H1) ≠ hash(H1, H0).
Из-за этого при построении доказательства нужно помнить, с какой стороны находится соседний узел.
Это усложняет реализацию алгоритма и добавляет необходимость хранить дополнительные данные.
Это очень легко исправить, просто отсортируйте два узла перед хешированием.
Для примера я дал Тх2, с учетом коммутируемости проверка будет выглядеть так: hash(hash(Hash2, Hash3), Hash01) = Root Hash
Когда вам не нужно беспокоиться о порядке, алгоритм проверки выглядит как простое свертывание массива: pub fn validate(&self, proof: &Vec<&[u8]>) -> bool {
proof[2.].
iter() .
fold( get_pair_hash(proof[0], proof[1], self.algo), |a, b| get_pair_hash(a.as_ref(), b, self.algo) ).
as_ref() == self.get_root()
}
Нулевой элемент — это хеш искомого объекта, первый — его сосед.
Пойдем! История была бы неполной без сравнения производительности, которое заняло у меня в несколько раз больше времени, чем реализация самого дерева.
Для этих целей я использовал фреймворк критерий .
Исходники самих тестов находятся здесь .
Все тестирование происходит через интерфейс ДеревоОбертка , который был реализован для обоих испытуемых: pub trait TreeWrapper<V> {
fn create(&self,
c: &mut Criterion, counts: Vec<usize>,
data: Vec<Vec<V>>, title: String);
fn find(&self,
c: &mut Criterion, counts: Vec<usize>,
data: Vec<Vec<V>>, title: String);
fn validate(&self,
c: &mut Criterion, counts: Vec<usize>,
data: Vec<Vec<V>>, title: String);
}
Оба дерева работают с одной и той же криптографией.
кольцо .
Я не собираюсь здесь сравнивать разные библиотеки.
Я взял самый обычный.
В качестве объектов хеширования используются случайно сгенерированные строки.
Деревья сравниваются на массивах разной длины: (500, 1000, 1500, 2000, 2500, 3000).
2500–3000 — примерное количество транзакций в блоке Биткойн на данный момент. На всех графиках ось X — количество элементов массива (или количество транзакций в блоке), а ось Y — среднее время выполнения операции в микросекундах.
То есть чем больше, тем хуже.
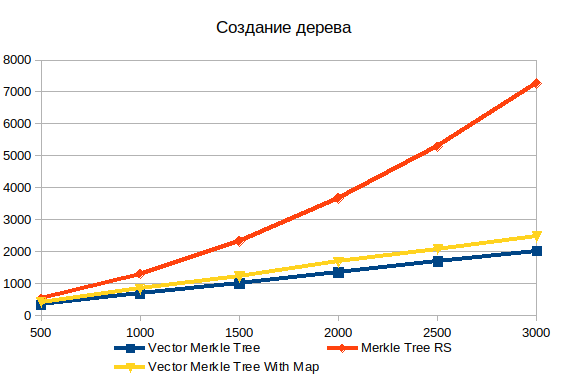
Создание дерева
Хранение всех данных дерева в одном массиве значительно превосходит граф объектов.Для массива из 500 элементов это в 1,5 раза, а для 3000 элементов уже в 3,6 раза.
Отчетливо виден нелинейный характер зависимости сложности от количества входных данных в стандартной реализации.
Я также добавил для сравнения два варианта векторного дерева: с Хэшмап и без этого.
Заполнение дополнительной структуры данных добавляет около 20%, но позволяет гораздо быстрее искать объекты при построении доказательства.
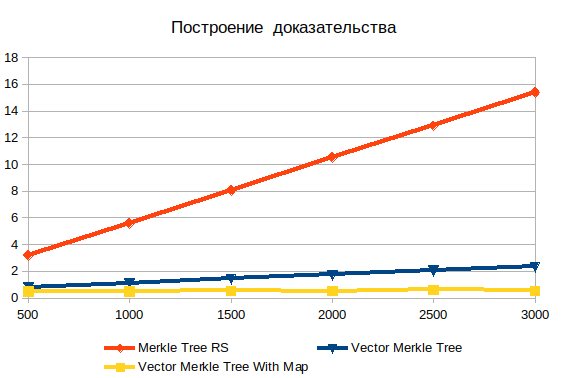
Построение доказательства
Это показывает очевидную неэффективность поиска в глубину.С увеличением входных данных становится только хуже.
Важно понимать, что искомые объекты представляют собой листы, поэтому сложность журнал (п) Не может быть.
Если данные предварительно хешируются, то время операции практически не зависит от количества элементов.
Без хеширования сложность растет линейно и представляет собой перебор методом перебора.
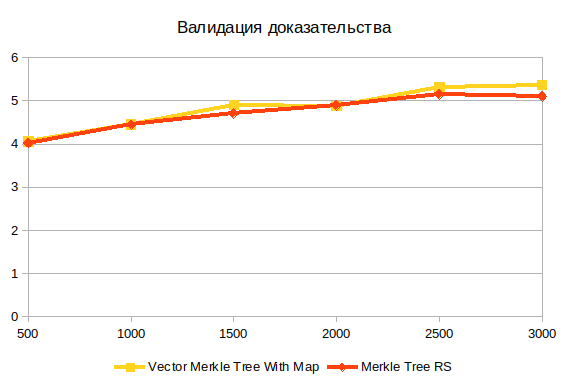
Проверка доказательств
Это последняя операция.Оно не зависит от структуры дерева, т.к.
работает с результатом построения доказательства.
Я считаю, что основная трудность здесь — вычисление хеша.
Нижняя граница
- Способ хранения данных оказывает большое влияние на производительность.
Когда все находится в одном массиве, это происходит намного быстрее.
И сериализовать такую структуру будет очень легко.
Общий объем кода также уменьшается.
- Объединение узлов с сортировкой значительно упрощает код, но не делает его быстрее.
- мне понравилась основа критерий .
Предоставляет четкие результаты со средними значениями и отклонениями, дополненными графиками.
Возможность сравнивать разные реализации одного и того же кода.
- Отсутствие наследства не сильно мешает жить.
- Макросы — мощный механизм.
я использовал их в тесты вашего дерева для параметризации.
Я думаю, если ими плохо пользоваться, можно сделать что-то, что не понравится.
- В некоторых местах компилятор утомлял проверками памяти.
Мое первоначальное предположение, что начать писать на Rust будет не так-то просто, оказалось верным.
- Более полное описание алгоритма дерева Меркла
- критерий — фреймворк для нагрузочного тестирования
- merkle.rs — самое популярное дерево для Rust
- вектор-меркле-дерево — моя реализация дерева
- merkle-tree-test-rs — проект для сравнения производительности двух библиотек

-
О Фотореализме
19 Oct, 24 -
Элмслев, Луи
19 Oct, 24 -
Рейтинг Mail.ru: Новые Возможности
19 Oct, 24 -
Авторское Право Против Культуры
19 Oct, 24 -
Полугодовой Солнечный Цикл Завершился.
19 Oct, 24 -
Гарнитура С Питанием От Солнца
19 Oct, 24


