Приятно, когда диаграмма помимо новых созвездий содержит что-то похожее на зависимость.
В этом случае мы строим модель, которая хорошо объясняет взаимосвязь между двумя переменными.
Но исследователь должен понимать не только то, как работать с данными, но и реальную историю, стоящую за ними.
В противном случае легко ошибиться.
Я расскажу вам о парадоксе Симпсона — одном из самых опасных примеров обманчивых данных, которые могут перевернуть общение с ног на голову.
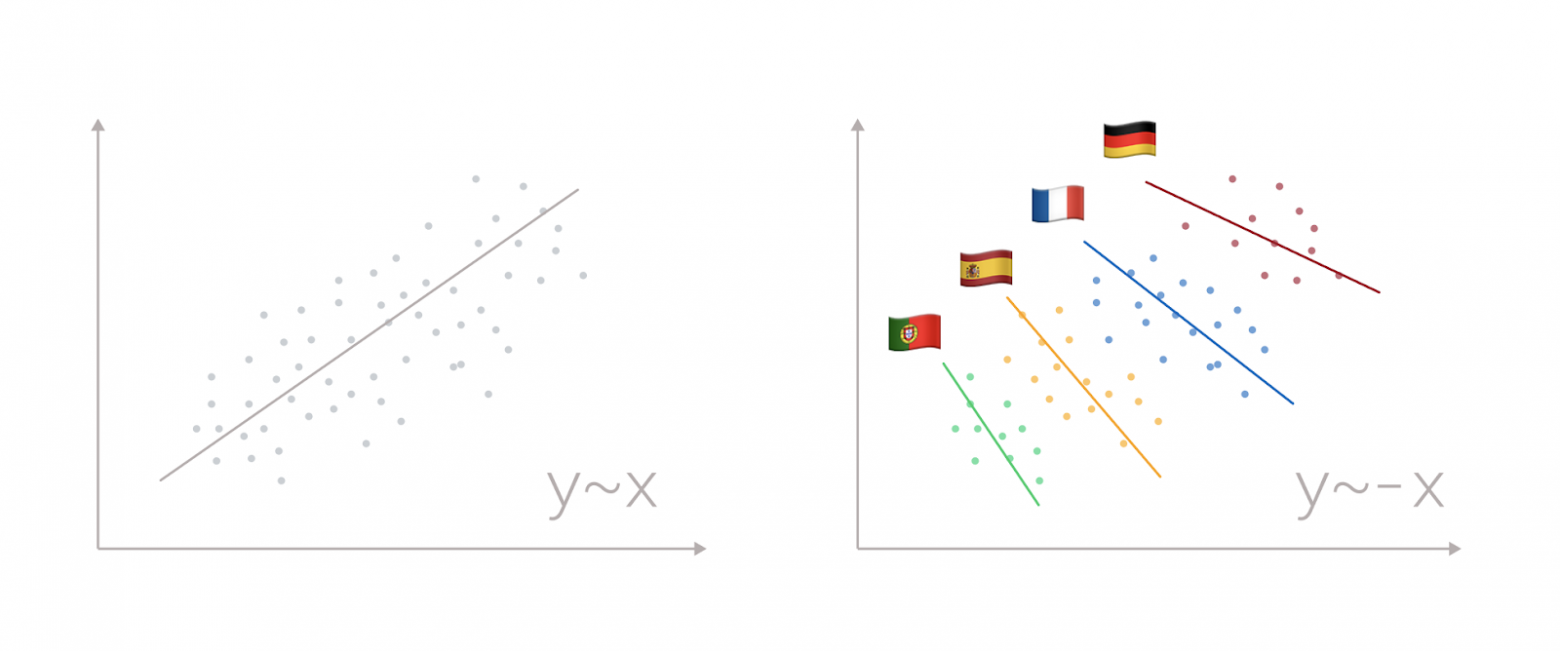
Давайте рассмотрим две условные переменные X и Y. Построив диаграмму, мы увидим облако, четко вытянутое от левого нижнего угла к правому верхнему, как на рисунке выше.
В эту картину прекрасно вписывается линейная регрессия, которая с относительно небольшой ошибкой поможет нам спрогнозировать значения: чем больше X, тем больше Y. Задача выполнена.
С первого взгляда.
Более опытный коллега порекомендует добавить на диаграмму разбивку по когортам: например, по странам.
Следуя его совету, мы увидим, что связь действительно есть, но она диаметрально противоположная – внутри одной страны чем больше Х, тем меньше Y. Это парадокс Симпсона: явление, при котором объединение нескольких групп данных с одинаковой зависимостью от направления приводит к изменению направления.
Пример 1: Дискриминация по признаку пола в Беркли
Самый известный пример парадокса Симпсона в реальном мире — это провал при поступлении в Беркли в 1973 году.Среди исследователей ходит слух, что над университетом даже судили, однако убедительных доказательств суда в Интернете найти не удалось.
Вот как выглядит статистика приема в университет за 1973 год:
| Пол | Приложения | Принял |
| Люди | 8442 | 3738 (44%) |
| Женщины | 4321 | 1494 (35%) |
Слишком большой, чтобы быть случайным.
Однако если разбить данные по отделам, картина изменится.
Исследователи обнаружили, что причина разницы заключалась в том, что женщины подали заявки на более конкурентоспособные области.
Кроме того, установлено, что из 85 факультетов 6 дискриминируют женщин в пользу и только 4 – против.
Разница возникает исключительно из-за различий в размерах выборки и масштабах конкуренции между департаментами.
Покажу на примере двух факультетов.
| Факультет | Пол | Приложения | Принял |
| А | Люди | 400 | 200 (50%) |
| А | Женщины | 200 | 100 (50%) |
| Б | Люди | 150 | 50 (33%) |
| Б | Женщины | 450 | 150 (33%) |
| Общий | Люди | 550 | 250 (45%) |
| Общий | Женщины | 650 | 250 (38%) |
Однако, поскольку абсолютное количество мужчин было больше на факультетах с более высокими показателями приема, при объединении данных оказывается, что в целом уровень приема мужчин выше.
Пример 2. Несбалансированный эксперимент A/B
Представьте, что вы проводите эксперимент A/B, чтобы повысить коэффициент конверсии вашей целевой страницы.Эксперимент проводился два дня, но в первый день сломался распределитель посетителей, и вариант Б получил больше посетителей.
На второй день эта проблема была устранена.
В результате получились следующие цифры:
| А | Б | |||
| Посетители | Конверсии | Посетители | Конверсии | |
| 1 день | 400 | 30 (7.5%) | 2000 | 140 (7%) |
| День 2 | 1000 | 60 (6.0%) | 1000 | 55 (5.5%) |
| Общий | 1400 | 90 (6.4%) | 3000 | 195 (6.5%) |
В этом примере неопытный исследователь развернет вариант Б для всего трафика, тогда как на самом деле коэффициент конверсии увеличится, если он воспользуется вариантом А.
Пример 3. Влияние посещения страницы на конверсию
На каждом веб-сайте есть страница, которая мотивирует людей покупать больше, чем другие.Допустим, мы создаем систему оценки посетителей и подбираем для нее факторы.
У нас есть страница «О нас», и мы предполагаем, что ее посещение увеличивает вероятность конверсии.
Давайте посмотрим на данные.
| Посетил страницу | ||
| Конверсия | Нет | Да |
| Нет | 4000 | 4800 |
| Да | 400 | 320 |
| Коэффициент конверсии | 9% | 6% |
Но если мы разобьем данные на две наиболее важные когорты в онлайн-маркетинге — пользователей настольных компьютеров и мобильных устройств, — мы увидим, что в каждой из них, по сути, вероятность конверсии увеличивается с количеством посещений страницы.
| мобильный | Рабочий стол | |||
| Посетил страницу | Посетил страницу | |||
| Конверсия | Нет | Да | Нет | Да |
| Нет | 1600 | 4200 | 2400 | 600 |
| Да | 40 | 180 | 360 | 140 |
| Коэффициент конверсии | 2% | 4% | 13% | 19% |
На практике в игру вступила третья переменная: платформа пользователя.
Поскольку он влияет не только на конверсию, но и на вероятность посещения страницы, в агрегированном состоянии он исказил данные таким образом, что привел нас к выводам, противоположным реальному поведению пользователей.

Что делать
При анализе данных вам необходимо понимать историю, стоящую за этим: что происходит в реальном мире, как это измерялось и переводилось в данные.Следовательно, специалист по данным в отделе маркетинга должен знать основы маркетинга, а специалист по данным в нефтегазовой отрасли должен кое-что знать о горнодобывающей промышленности.
Это поможет избежать большого количества потенциальных ошибок, не последней из которых является ошибка агрегирования, вызванная парадоксом Симпсона.
Следующие характеристики данных обычно приводят к парадоксу Симпсона:
- Наличие значимых когорт, способных влиять на значения зависимой (Y) и независимой (X) переменных;
- Когортный дисбаланс.
Считать, что все данные всегда нужно разбивать на когорты – тоже неправильный подход, ведь зачастую именно агрегированные данные позволяют построить наиболее точную модель.
Кроме того, любые данные можно разбить таким образом, чтобы получить ту связь, которую нам хотелось бы получить.
Правда, никакого практического применения это не будет иметь — когорты должны быть обоснованы.
Для онлайн-маркетинга одним из важнейших выводов является необходимость проверки корректности работы сплиттера в A/B-экспериментах.
Группы пользователей в каждом тестовом примере должны быть примерно одинаковыми.
Речь идет не только об общем количестве пользователей, но и об их структуре.
При подозрении на проблемы когорты следует сначала проверить на наличие следующих характеристик:
- Демографические характеристики;
- Географическое распределение;
- Источник трафика;
- Тип устройства;
- Время посещения.
Дж.
Бикель, ?.
А.
Хаммель и Дж.
В.
О'Коннелл (1975) «Сексуальная предвзятость при поступлении в аспирантуру: данные Беркли»
Теги: #Машинное обучение #математика #Статистика в ИТ #Интеллектуальный анализ данных #статистика #Парадокс Симпсона
-
Бесплатная Mmo — Лучший Способ Играть
19 Oct, 24 -
Интервью С Экспертами - Часть 2
19 Oct, 24 -
Разделение Чата И Поиск В Telegram
19 Oct, 24 -
Семинар По Вредоносному Коду На Javascript
19 Oct, 24 -
Chromium: Шестой Обзор Проекта И 250 Ошибок
19 Oct, 24


