Тема защиты авторских прав стала чрезвычайно популярной в настоящее время; появилось множество способов предотвращения нелицензионного дублирования.
Одним из таких методов является цифровой водяной знак (Digital Watermarking, Digital Watermark), добавляющий к исходной информации (цифровому изображению, видео или звуковому файлу) некоторые скрытые маркеры, устойчивые к любым атакам.
Цифровые водяные знаки в основном используются для установления факта нарушения авторских прав, но, конечно же, сфера применения цифровых водяных знаков этим не ограничивается.
Например, цифровые водяные знаки могут использоваться для передачи конфиденциальной информации, проверки подлинности электронных документов и в ряде других приложений.
Во многих приложениях и сайтах реализована защита видеопродукции с помощью цифровых записей, где конструируются несколько идентификационных тегов, один из тегов вводится в видеоряд, тег извлекается из пиратской копии видеоряда, а члены коалиции поиск с использованием извлеченного тега.
Рассмотрим реализацию и проверку цифрового водяного знака на примере алгоритма дискретного вейвлет-преобразования изображения.
Дискретное вейвлет-преобразование
Дискретное вейвлет-преобразование разлагает сигнал на взаимно ортогональный набор вейвлетов (математических функций, позволяющих анализировать различные частотные составляющие данных), что является основным отличием от непрерывного вейвлет-преобразования.Вейвлет может быть построен на основе функции масштабирования, которая описывает его свойства масштабируемости.
Ограничение состоит в том, что масштабная функция должна быть ортогональна своим дискретным преобразованиям, что накладывает на них некоторые математические ограничения:
где - масштабный коэффициент (у нас он будет равен 2), при этом площадь под функцией должна быть нормированной, а масштабирующая функция должна быть ортогональной, следовательно:
Введя некоторые дополнительные условия (поскольку указанные выше ограничения не приводят к единственному решению), мы можем получить результат этих уравнений, т.е.
конечный набор коэффициентов
которые определяют функцию масштабирования, а также вейвлет. Затем набор вейвлетов образует ортонормированный базис, который мы используем для разложения, обычно это всего лишь несколько коэффициентов.
будет отличным от нуля, что упрощает расчеты.
Схема алгоритма
Давайте рассмотрим схему работы над растровым изображением.
Давайте определим двумерный массив, имеющий размеры
, обозначающий яркость конкретной координаты по одному из цветов (
— яркость пикселей с координатами
для всех
) Далее рассмотрим шаг: создаем четыре массива (модель двумерного вейвлет-преобразования):
Для всех
.
Здесь
означает отклонение яркости точки с координатами
от среднего арифметического яркостей двух соседних по горизонтали точек
И
(Рисунок 1),
означает отклонение яркости точки с координатами
от среднего арифметического яркостей двух соседних по горизонтали точек
И
(рис.
2),
означает отклонение яркости точки с координатами
от среднего арифметического яркостей четырех соседних точек.
(рис.
3) 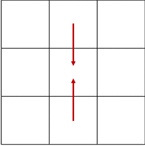
Рис.
2 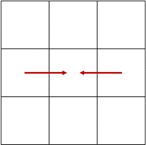
Рисунок 1 
Рис.
3 Далее мы «обновляем» точки массива
:
Обновление необходимо для того, чтобы гарантировать, что средняя энергия изображения
(его средняя яркость) равнялась средней яркости исходного массива.
Очевидно, образ
, и в результате он обязательно восстанавливается.
Также стоит отметить, что каждый раз, когда мы вычисляем новые элементы
,
,
, мы можем уже не помнить те, которые использовали для их расчета (
,
,
).
Это означает, что наш алгоритм не требует дополнительной памяти.
Выполняем наши действия до тех пор, пока наш массив не достигнет размера
.
То есть теперь у нас тоже есть наборы
,
,
;
,
,
;.
;
,
,
Заметь
,
,
влияют только
пикселей, таким образом, каждый шаг соответствует разной степени резкости (детализации).
Например, для
каждый коэффициент влияет только на 3 пикселя, если
затем на 5 и т. д. Давайте теперь попробуем встроить нашу цифровую картину в изображение, для этого выберем
- «видимость» водяного знака, резкость -? шаг и массив, или , в который мы введем водяной знак.
Пусть это будет для уверенности
, затем замените его массивом
, такой, что:
Здесь
, и как следствие
, имеет тот же размер, что и
.
можно назвать коэффициентами вейвлет-преобразования другого изображения
.
Выполним обратное вейвлет-преобразование и получим новое изображение, назовем его
.
Теперь поговорим о том, как автор, имея лишь
, или еще проще, сами коэффициенты
, их можно легко вычислить, зная все остальное), параметр, в который был заложен массив, и видимость
, смогут проверить наличие центрального выставочного центра.
Зная исходное изображение, мы можем проверить, помечено ли наше изображение, просто сравнивая разницу коэффициентов и массива.
Теперь рассмотрим случай, когда мы не знаем исходное изображение и по тем же причинам
.
Тогда мы не можем точно сказать, использовалась ли здесь ЦЭЗ, но можем оценить вероятность ее обнаружения.
Для этого будем считать, что наше изображение осмысленно, то есть не представляет собой хаотическое распределение яркостей пикселей.
Соответственно, массив
, предположительно несущий водяной знак и напрямую связанный с изображением, также демонстрирует некоторую упорядоченную структуру.
Значит что
прежде чем добавить его
представляла собой более-менее упорядоченную структуру, а это значит, что нам необходимо
(с точностью до коэффициента
) ввести меру порядка – сложность.
Вариация функции вполне подойдет. Действительно, чем меньше резких изменений функции, тем меньше ее вариация.
Для двумерного массива введем аналог вариации:
Давайте разберемся, как можно применить эту функцию: как описано ранее, если
- результат применения водяного знака (
), то это будет сложнее, чем
, что означает, что оно будет выполнено:
Для более надежной работы алгоритма можно ввести порог, после которого будем считать, что цифровой водяной знак обнаружен, если
где ценность
будет соответствовать максимально возможному увеличению вариации при добавлении
в массив
, А
-параметр подбирается экспериментально.
Заключение
Стоит сказать, что данный алгоритм, основанный на дискретном вейвлет-преобразовании, является лишь одним из многих способов, с помощью которых можно реализовать цифровой водяной знак и проверить его наличие в файле.Например, вы можете использовать кодировку сдвига строки для текста, водяные знаки домена DCT для изображений и кодировку наименее значимого значения для аудио.
Преимущество приведенного алгоритма в том, что такие водяные знаки устойчивы к сжатию JPEG (для изображений) и некоторым другим искажениям, поэтому этот метод остается актуальным и по сей день.
Теги: #информационная безопасность #Алгоритмы #Криптография #алгоритм #изображения #Wavelet #CVS #Watermark
-
Не Нарушайте Мою Конфиденциальность
19 Oct, 24 -
Выпущена Opensuse 12.3
19 Oct, 24 -
Я Хочу Знать Все: Бизнес-Анализ. Часть 1
19 Oct, 24 -
Новый Подход В Китае
19 Oct, 24 -
Незамаскированная Zfs
19 Oct, 24 -
Dell И Tlc 3D Nand: Что-То Новое
19 Oct, 24 -
«Звездные Войны» Берут Паузу – Комментарии
19 Oct, 24


