Сегодня компьютеры решают практически любую проблему.
Они работают и приносят пользу практически во всех отраслях.
Но давайте посмотрим, что такое компьютер.
Это машина, которая манипулирует числами.
Подобные манипуляции – это практически все, что они могут сделать.
Поэтому тот факт, что они решают так много проблем, просто манипулируя числами, кажется почти волшебным.
Давайте посмотрим, откуда берутся цифры, к чему они могут привести и как они работают. Статья основана на докладе Дугласа Крокфорда с июньской конференции.
HolyJS 2017 в Санкт-Петербурге (презентацию доклада можно найти здесь )
Пальцы
Начнем с пальцев.Пальцы намного старше цифр.
Человек развил свои пальцы, чтобы лучше лазить по деревьям и собирать фрукты.
И он был по-настоящему счастлив, занимаясь этим миллионы лет.
Инструменты
Но климат изменился, деревья стали исчезать.Мужчине пришлось спуститься на землю, пройтись по траве и искать другие источники пищи.
А пальцы были нужны для манипулирования инструментами, например палкой.
С его помощью можно было копать землю в поисках клубней.
Другой пример инструмента — камень, который позволяет раздавливать клубни, чтобы они стали достаточно мягкими, чтобы их можно было есть (наши маленькие обезьяньи зубы не позволяют нам есть все; нам пришлось научиться готовить, чтобы выжить).
Со временем человек приобретал опыт обращения с инструментами.
И эти инструменты повлияли на нашу эволюцию, поэтому мы продолжали их обновлять.
Вскоре мы научились делать ножи из вулканического стекла и со временем научились управлять огнем.
Теперь человек знал, как сажать семена в землю и выращивать себе еду.
Получив новые знания, люди начали собираться в более крупные сообщества.
Мы перешли от семей и кланов к городам и нациям.
Общество росло и возникла проблема отслеживания всей человеческой деятельности.
Чтобы ее решить, человеку пришлось придумать аккаунт.
Проверять
Оказывается, наш мозг не очень хорошо запоминает многие числа.Но чем сложнее становилось общество, тем больше вещей нужно было помнить.
Поэтому человек научился делать насечки на дереве и надписи на стенах.
Возникли идеи нанизывать орехи на веревочки.
Но мы еще забыли, что именно означают эти цифры.
Поэтому пришлось придумать письменность.
Письмо
Сегодня мы используем письмо для решения многих задач: для писем, для законов, для литературы.Но сначала это были рукописи.
Я считаю изобретение письменности самым важным открытием, когда-либо сделанным человеком, и это произошло трижды.
Первые следы письменности были обнаружены на Ближнем Востоке.
Многие умные люди полагают, что это произошло в Месопотамии.
Я думаю, это произошло в Египте.
Кроме того, письменность была изобретена в Китае и Америке.
К сожалению, последняя из упомянутых цивилизаций не пережила испанское вторжение.
Давайте подробнее рассмотрим некоторые исторические системы счисления.
Египет
Вот как выглядели цифры в Египте.

У египтян была десятичная система.
Для каждой 10-й степени имелся свой иероглиф.
Палка представляла собой единицу, кусок веревки — 100, палец — 10 000, а парень с поднятыми руками — миллион (это демонстрирует некоторую математическую изощренность, поскольку у них был символ, который не представлял собой абстрактное понятие «многие»).
, а именно "миллион" - ни больше, ни меньше).
Египтяне придумали много чего другого: треугольник 3 на 4 на 5 с прямым углом (они знали, для чего нужен этот угол), действительно умную систему работы с дробями.
У них было приближение числа Пи и многого другого.
Финикия
Египтяне научили своей системе финикийцев, живших на территории современного Ливана.Они были очень хорошими мореплавателями и торговцами – плавали по Средиземному морю и части Атлантики.
Переняв у египтян довольно сложную систему счисления, они упростили ее.
Используя письменность, состоящую только из согласных, они сократили набор символов с тысяч, имевшихся у египтян, до пары десятков, которые было гораздо проще использовать.
И они научили своей системе людей, с которыми торговали, особенно греков.
Греция

Греки взяли финикийскую систему и усовершенствовали ее, добавив гласные.
Поэтому теперь они могли правильно записать все слова.
С этого времени греческий алфавит содержит 27 букв.
Греки использовали тот же набор символов для записи чисел.
Они взяли первые 9 букв алфавита для обозначения чисел от 1 до 9, следующие 9 букв для обозначения десятков от 10 до 90 и еще 9 букв для сотен от 100 до 900. Свою систему они передали римлянам.
Рим

Но римляне по-прежнему основывали свою систему счисления на египетской.
Хотя они переняли греческий подход – использовали буквы вместо иероглифов.
Они также добавили некоторые нововведения, чтобы сделать цифры немного компактнее.
Одна из проблем египетской системы заключалась в том, что для записи числа 99 требовалась последовательность из 18 символов.
Римляне хотели сократить рекорд. Для этого придумали символы, обозначающие половину десяти или полста (тысячи).
У них был один, представленный символом I (или палкой), 10 — X (связка палочек, соединенных вместе), а 5 — буквой V, что представляет собой всего лишь X пополам.
Еще одним нововведением стало добавление в систему счисления вычитания.
До сих пор системы были аддитивными.
Число представлялось суммой всех символов.
Но у римлян была идея, что определенные символы (в определенных позициях) могут уменьшать число.
Китай
Тем временем в Китае происходили действительно интересные вещи.
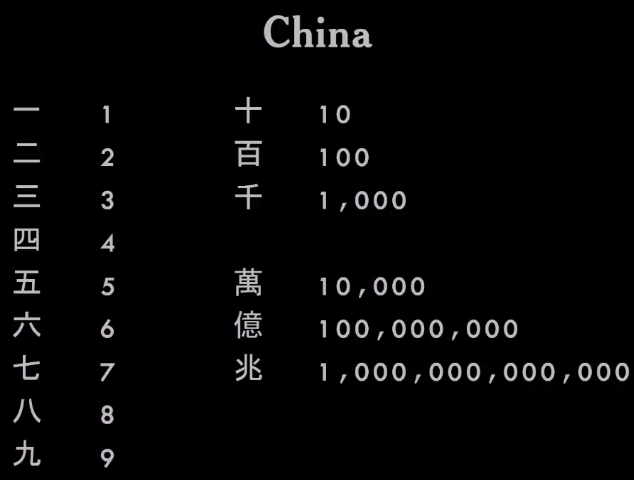
У них была другая система, в которой использовались символы от 1 до 9 и набор множителей или модификаторов.
Таким образом, числа любого размера и сложности можно было записать, просто сложив иероглифы.
Очень элегантная система.
Индия
Самый большой скачок произошел в Индии.

Математики в Индии придумали идею нуля — числа, которое ничего не представляет. И они придумали использовать это по позиционному принципу.
Для отображения чисел использовалось всего 10 символов, но их можно было комбинировать для создания любого числа.
Это была действительно важная идея.
Повторение идеи
Индийцы передали свою систему персам.Они назвали это индийскими цифрами.
А от персов идея пришла к арабам.
В свою очередь арабы передали его европейцам, которые назвали такой способ записи арабскими цифрами.
Это основная система счисления, которую сегодня использует большая часть мира.
Самое замечательное то, что независимо от того, на каком языке вы говорите, вы можете понять эти цифры.
Написание числа так же универсально, как и человеческое общение.
Написание чисел и математика
Вот одно и то же число, записанное во всех упомянутых системах.

И все эти системы работали.
Они использовались ключевыми странами и империями на протяжении веков.
Поэтому трудно утверждать, что одна из этих систем лучше другой.
Единственное преимущество индийской системы перед всеми остальными заключалось в том, что можно было взять столбец чисел и сложить их, не используя счеты — имея лишь ручку, бумагу и немного тренированный мозг.
В любой другой системе это было бы нелегко сделать.
Сегодня это не имеет значения, потому что у нас есть компьютеры.
Поэтому нет однозначного ответа, почему мы до сих пор используем эту систему.
В его использовании могут быть некоторые преимущества, которые я не могу себе представить, например, набор телефонного номера.
Кажется, что это будет довольно сложно сделать, используя римские цифры.
Но я не помню, когда в последний раз набирал номер телефона.
Так что, возможно, это уже не имеет значения.
Важная идея заключается в том, что индийские числа научили нас математике.

Это позиционная система.
Вы можете взять числа и разместить их на числовой прямой, а затем сложить числа в каждой позиции, умножив их на 10 в степени, соответствующей номеру этой позиции.
Оказывается, индийские числа — это сокращение полиномов.
А полином — действительно важное понятие в математике.
У нас есть способ записывать числа.
В других системах такого не было.
Целые числа
Эта система также допускала отрицательные числа.

Мы могли бы написать число со знаком минус, обозначающим отрицательные вещи.
Эта концепция не имела смысла в других системах счисления.
О негативных вещах в Египте мы говорить не могли, не было смысла.
Но мы можем сделать это в индийской системе.
И оказывается, что с отрицательными числами происходит много интересного.
Вещественные числа
Мы можем взять числовой ряд и продолжить его назад до бесконечности.Используя эти обозначения, мы получаем действительные числа.

Другие системы счисления также могут работать с дробями.
Но это всегда были особые случаи.
Используя индийскую систему, мы можем записывать дроби так же, как целые числа — просто требуется немного дисциплины в обращении с десятичными знаками.
В оригинальных индийских обозначениях положение разделителя указывалось линией вверху.

Но с годами разделительный символ изменился.
В разных странах существуют свои конвенции о том, как писать.
В некоторых культурах используется десятичная точка, в других — запятая.
И долгое время это не имело значения.
Вы были в своей стране и могли правильно или неправильно написать цифры.
Но это становится проблемой, когда у вас есть Интернет, потому что теперь цифры повсюду.
Записанный вами номер можно увидеть где угодно.
И каждый увидит разное – может возникнуть путаница.

Например, в зависимости от того, где вы находитесь и как учились, первое число на картинке вы можете прочитать как 2048 или 2 и 48 тысячных.
И это может быть действительно серьезной ошибкой, особенно когда дело касается финансов.
Так что я предсказываю, что мир рано или поздно найдет способ выбрать один из вариантов записи.
Потому что в этой путанице нет никакой ценности.
Однако сложность выбора между вариантами состоит в том, что ни один из них не является явно лучшим.
Как мир выберет? Я предвижу, что ты примешь это решение.
И вы выбираете десятичную точку, потому что именно ее использует ваш язык программирования.
И все числа в мире в конечном итоге проходят через компьютерные программы.
В конце концов вы просто решите упростить его.
База
Все рассмотренные выше системы имеют основание 10. Именно так записывались числа на Ближнем Востоке и в Китае.Они не общались друг с другом, а взяли основание 10. Как это произошло? Они просто считали пальцы на обеих руках.
И это сработало.
Но есть и другие культуры, которые писали числа по-другому.
Например, в Америке была система счисления с основанием 20. Знаете, как они ее придумали? Думаю, это очевидно: они считали пальцы не только на руках, но и на ногах.
И это тоже сработало.
У них была развитая цивилизация.
Они провели довольно много вычислений, но использовали систему счисления по основанию 20. Некоторые культуры использовали основание 12. И мы до сих пор можем видеть их следы в нашем мире.
Например, основание наших часов равно 12. У нас все еще есть 12 дюймов в футах.
Мы научились этому у англичан и до сих пор не можем отказаться от использования подобных усложнений.
Компромиссы: 60
Шумеры использовали 60-е счисление.А мы до сих пор придерживаемся 60-го, верно? Так мы считаем время и проводим географические измерения.
Географические приложения должны использовать систему координат Base-60. Это добавляет ненужную сложность.
Как появилось основание 60? Я думаю, когда города разрослись, они поглотили множество мелких поселений, объединив их в более крупные.
В какой-то момент они попытались объединить сообщество, использовавшее основание 10, с сообществом, принявшим основание 12. Наверняка был какой-то король или комитет — кто-то должен был решить, как их объединить.
Правильным вариантом было использовать основание 10. Второй вариант — развивать с основанием 12. Но вместо этого выбрали худший вариант — использовать основание, которое является наименьшим общим кратным.
Причина, по которой было принято это решение, заключается в том, что комитет не смог решить, какой вариант лучше.
Они пришли к компромиссу, который, по их мнению, был похож на то, чего хотели все.
Но дело не в том, кто чего хочет. Следует отметить, что комитеты по-прежнему принимают подобные решения каждый раз, когда выпускают стандарты.
Бинарная система
Действительно интересная вещь в базе — это появление двоичной системы.
Мы можем взять индийскую систему и просто заменить 10 на 2. 
Таким образом, мы можем представить все с помощью битов.
И это был действительно важный шаг вперед, поскольку он позволил изобрести компьютер.
Если мы начнем говорить о компьютерах, использующих двоичный формат, нам необходимо запомнить знак числа.
Существует три способа записи и отображения знака:
- Значение знака (Знаковое представление величины).
В этом случае мы просто добавляем к числу дополнительный двоичный бит и решаем, в каком состоянии этот бит соответствует положительному числу, а в каком — отрицательному числу.
Не имеет значения, поместим ли мы этот бит спереди или сзади (это всего лишь вопрос договоренности).
Недостатком этого метода является наличие двух нулей: положительного и отрицательного, что не имеет смысла, так как ноль не имеет знака.
- Первое дополнение (дополнение до единицы), при котором мы не выполняем побитовую операцию над числом, чтобы сделать его отрицательным.
Помимо двух нулей (положительного и отрицательного – как в предыдущем варианте), в этом представлении есть проблема переноса: при сложении двух чисел, представленных таким образом, для получения правильного результата необходимо прибавить 1 бит в позиции конец.
Но в остальном это работает.
- Второе дополнение (дополнение двойки), благодаря которому удалось обойти проблему переноса.
Отрицательное N представляется не как поразрядное отрицание положительного N, а как +1. Помимо отсутствия проблемы переноса, мы получаем всего один ноль, что очень хорошо.
Но при этом мы получаем дополнительное отрицательное число.
И это проблема, потому что вы не можете получить абсолютное значение этого числа — вместо этого вы получите то же самое отрицательное число.
Это потенциальный источник ошибок.
Я думаю, нам следует взять это дополнительное число (отрицательный 0 или дополнительное отрицательное число из дополнения ко второму) и превратить его в сигнал о том, что это вообще не число.
Таким образом, это позволит нам избежать проблемы, которая возникает в Java: если мы используем метод indexOf для поиска строки в другой строке, а если он ее не находит, Java не может об этом сигнализировать.
Потому что эта дурацкая система может возвращать только int, а int может представлять только целые числа.
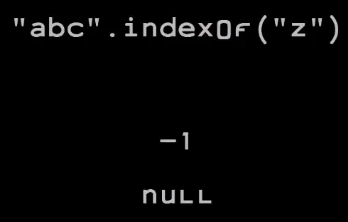
Чтобы обойти эту проблему, придумали сомнительный компромисс: вернуть минус единицу.
Но, к сожалению, если вы просто возьмете возвращаемое значение и поместите его в другую формулу, вы можете получить неверный результат. Если метод вернул нулевое значение, это можно было бы обнаружить в дальнейшем, и у нас было бы меньше шансов получить неверный результат вычислений.
Типы
Давайте подробнее рассмотрим типы, используемые в наших языках.
интервал
У нас есть много языков, которые имеют int32 под разными именами.Если мы добавим два числа int32, какого типа будет результат? Ответ — int33, потому что вы можете добавить число, немного большее, чем int32. Здесь Java ошибается.
Java говорит, что это int32.
Другой пример — умножение int32 на int32. Что мы получим в результате? Похоже на int63. 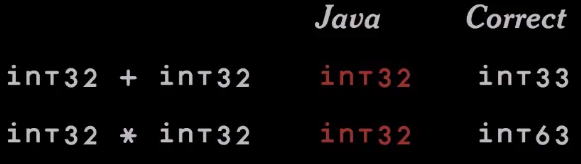
Когда обычная оценка приводит к результату, выходящему за рамки области видимости, мы получаем переполнение.
И наши процессоры это знают. Например, в архитектуре Intel процессор имеет флаг переноса, содержащий 33-й бит. Также в архитектуре Intel, если вы выполняете умножение 32-битных чисел, вы получаете 64-битный результат. Те.
есть регистр, содержащий нужные вам «лишние» 32 бита.
И есть флаг переполнения, который устанавливается, если необходимо игнорировать умножения высокого порядка.
Сообщает, что произошла ошибка.
К сожалению, Java не позволяет вам получить эту информацию.
Она просто выбрасывает все, что является проблемой.
Что должно произойти при переполнении? Здесь есть несколько вариантов:
- мы можем хранить значение null, что, на мой взгляд, очень разумно;
- или максимально возможная часть (насыщение).
Это может быть разумно при обработке сигналов и компьютерной графике.
Однако не стоит делать это в финансовых приложениях;
- вы можете выдать ошибку - машина должна выдать исключение или что-то должно произойти.
Программное обеспечение должно понимать, что в расчетах произошла путаница и ситуацию необходимо исправить;
- некоторые говорят, что программу следует остановить.
Это довольно резкая реакция, но этот вариант сработал бы, если бы машина не просто остановилась, а каким-то образом сообщила, что что-то не так.
Именно это и делает Java и большинство наших языков программирования.
Те.
они предназначены для увеличения частоты ошибок.
Разбиение чисел на значения из разных регистров
Первые компьютеры работали с целыми числами.Но машины были построены и запрограммированы математиками, и они хотели работать с действительными числами.
Поэтому была разработана арифметика, где действительное число представляется целым числом, умноженным на некоторый масштабный коэффициент. Если у вас есть два числа с одинаковыми масштабными коэффициентами, вы можете просто сложить их, но если они имеют разные масштабные коэффициенты, вам придется изменить хотя бы одно из них для выполнения простых операций.
Поэтому перед выполнением каких-либо операций необходимо сравнить масштабный коэффициент. А запись стала немного сложнее, потому что нужно было в конце ставить дополнительный масштабный коэффициент. И деление усложняется, потому что приходится учитывать коэффициент масштабирования.
В результате люди начали жаловаться, что это сильно усложняет программирование и делает его очень подверженным ошибкам.
Кроме того, было сложно найти оптимальный масштабный коэффициент для любого приложения.
В качестве решения этих проблем кто-то предложил создать числа с плавающей запятой, которые могли бы представлять собой аппроксимации действительных чисел, используя два компонента: само число и запись о том, где внутри него находится десятичная точка.
Используя эти обозначения, вы можете относительно легко выполнять сложение и умножение.
Таким образом, вы получите наилучшие результаты, которые машина может обеспечить, с гораздо меньшим количеством программирования.
Это было большим достижением.
Первая форма записи числа с плавающей запятой выглядит примерно так: у нас есть некоторое число, значение которого увеличено на 10 в степени логарифма масштабного коэффициента.

Этот подход был реализован в программном обеспечении первых машин.
Это работало, но крайне медленно.
Сами машины были очень медленными, и все эти переоборудования только ухудшали ситуацию.
Неудивительно, что возникла необходимость интегрировать это в железо.
Следующие поколения машин уже понимали вычисления с плавающей запятой на аппаратном уровне, однако для двоичных чисел.
Переход с десятичного на двоичный формат был вызван потерей производительности из-за деления на 10 (что иногда приходится делать для нормализации чисел).
В двоичной системе вместо деления достаточно было просто переместить разделитель – это практически «бесплатно».
Вот как выглядит стандарт с плавающей запятой в двоичном виде: 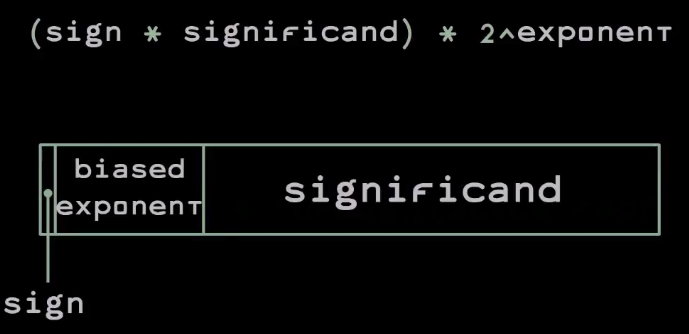
Число записывается с использованием знакового бита мантиссы, который равен 0, если число положительное, и 1, если отрицательное, самой мантиссы, а также смещенной экспоненты.
Смещение здесь является своего рода оптимизацией — оно позволяет выполнить целочисленное сравнение двух значений с плавающей запятой, чтобы увидеть, какое из них больше.
Однако с этим обозначением есть проблема: 0,1 + 0,2 не равно 0,3. 
Результат близок, но он неверен.
Давай посмотрим что происходит. 
Представим себе числовой ряд. 0,1 — это примерно 1/16+1/32, но немного больше, поэтому нам понадобится еще несколько бит. Двигаясь вниз по числовой прямой, мы получим бесконечно повторяющуюся серию 0011, похожую на то, что происходит с 1/3 в десятичной дроби.

Это здорово, если у вас есть бесконечное количество свободных битов.
Если продолжать эту последовательность до бесконечности, вы получите именно то, что вам нужно.
Но у нас нет бесконечного числа битов.
В какой-то момент нам придется отрезать этот хвост. И конечная ошибка будет зависеть от того, где вы срезали.
Если вы вырежете до 0, вы потеряете все последующие биты.
Поэтому ваш результат будет немного меньше необходимого.
Если отрезать раньше 1, то по правилам округления нужно переместить единицу, то результат будет немного больше.

И можно надеяться, что при расчетах вы допустите небольшую ошибку в одну и другую сторону, и в результате ошибки уравновесятся.
Но этого не происходит. Вместо этого ошибка накапливается — чем больше вычислений мы делаем, тем хуже результат. Всякий раз, когда мы представляем константу в программе, написанной на языке, или в данных, как десятичную дробь, мы не получаем это точное число.
Мы получаем приблизительное значение этого числа, поскольку работаем с системой счисления, которая не может точно представлять десятичные дроби.
А это нарушает закон ассоциации.
Закон ассоциации действительно важен при алгебраическом манипулировании выражениями в программах.
Но это терпит неудачу, если входные/выходные данные и промежуточные результаты вычислений не могут быть точно представлены.
А поскольку ни одно из наших чисел не представлено точно, все расчеты неверны! Это означает, что (A + B) + C — это не то же самое, что A + (B + C), и порядок выполнения вычислений может изменить результат. Эта проблема не нова.
Это было известно ещё во времена развития вычислений с плавающей запятой в двоичной системе — таким образом разработчики пошли на компромисс.
В то время существовало две школы информатики:
- те, кто занимался научной работой, писали на Фортране, используя числа с плавающей запятой в двоичной системе;
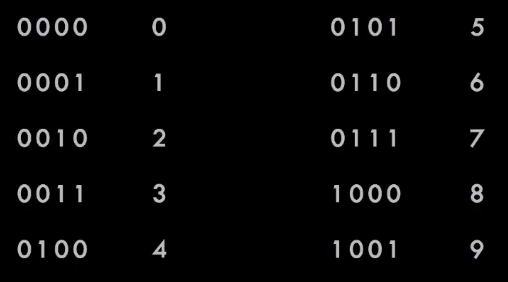
- те, кто занимается бизнесом, писали Кобол, используя двоично-десятичный код (BCD).
Код BCD выделяет 4 бита для каждого числа и выполняет обычный десятичный счет (с использованием обычной арифметики).
Компьютеры дешевеют и теперь могут решить практически любую проблему, но мы все еще застряли в модели двух разных миров.
Другая проблема с представлением числа в двоичном формате с плавающей запятой — сложность преобразования текста.
Берем кусок текста и превращаем его в число; затем мы берем число и преобразуем его обратно в фрагмент текста.
Это нужно сделать правильно, эффективно и без сюрпризов, используя как можно меньше цифр.
Оказывается, при такой записи это очень сложная задача, дорогая с точки зрения производительности.
Проблема с типами
В большинстве современных языков программирования существует путаница из-за ошибочных типов данных.Например, если вы пишете на Java, каждый раз, когда вы создаете переменную, свойство или параметр, вам нужно выбрать правильный тип: Bite, Char, Short, Int, Long, Float, Double. И если вы выберете неправильно, программа может не работать.
Причём ошибка проявится не сразу и не будет видна в тестах.
Это проявит себя в будущем, когда произойдет переполнение и плохие вещи.
Что может случиться? Одним из самых драматичных примеров стал провал Aryan 5. Это ракета, отправленная Европейским космическим агентством.
Он резко отклонился от курса и через несколько секунд после запуска взорвался.
Причиной этого стала ошибка в программном обеспечении, написанном на языке Ada. Здесь я перевел ошибку на Java: 
У них была переменная, определяющая горизонтальное смещение.
И ее перевели в Шорт, который был переполнен.
Результат, появившийся в Short, был неверным.
Но оно было отправлено в систему наведения и полностью ее сбило с толку, так что курс восстановить уже невозможно.
Эта ошибка оценивается примерно в полмиллиарда долларов.
Полагаю, вы не совершили ошибку, которая стоила полмиллиарда долларов.
Но могли бы (технически это все еще возможно).
Поэтому нам следует попытаться создать системы письменности и языки, позволяющие избежать подобных проблем.
ДЕКАБРЬ64
С точки зрения выбора типа данных при объявлении переменных JavaScript намного лучше — язык имеет только один числовой тип.Это означает, что целый класс ошибок можно автоматически избежать.
Единственная проблема заключается в том, что этот тип неверен, поскольку это двоичное число с плавающей запятой.
И нам нужны десятичные числа с плавающей запятой, потому что.
иногда мы складываем деньги и хотим, чтобы результат имел смысл.
Предлагаю исправить этот тип.
Моё исправление называется DEC64, это современная система записи десятичных чисел с плавающей запятой.
Я рекомендую DEC64 как единственный числовой тип в языках прикладного программирования в будущем.
Потому что, если у вас есть только один числовой тип, вы не сможете совершить ошибку, выбрав неправильный тип (я думаю, это принесет гораздо больше пользы, чем то, что мы можем получить, имея несколько типов).
Аппаратная реализация DEC64 позволяет добавлять числа за один цикл, что снижает проблемы с производительностью при использовании старых типов.
Преимущество DEC64 в том, что в этой записи основные операции с числами работают так, как привыкли люди.
А устранение числовой путаницы уменьшает количество ошибок.
Кроме того, преобразование чисел DEC64 в текст и обратно является простым, эффективным и не содержит сюрпризов.
На самом деле это немного сложнее, чем преобразование целых чисел в текст и обратно — вам просто нужно следить за тем, где находится десятичная точка, и вы можете удалить лишние нули с обоих концов, а не только с одного.
DEC64 может точно представлять десятичные дроби длиной до 16 цифр, чего достаточно для большинства наших приложений.
Вы можете представлять числа от 1*10 -27 до 3 со 143 нулями.
DEC64 очень похож на оригинальные числа с плавающей запятой, разработанные в 40-х годах.
Число представляется в виде двух чисел, упакованных в 64-битное слово.
Коэффициент представлен 56 битами, а индикатор — 8 битами.

Причина, по которой показатель степени находится в конце, заключается в том, что в архитектуре Intel мы можем распаковать такое число практически бесплатно.
Это помогает в реализации программного обеспечения.
Если вы хотите ознакомиться с программной реализацией DEC64, ее можно найти по адресу GitHub .
И если вы думаете о разработке следующего языка программирования, я настоятельно рекомендую вам рассматривать DEC64 как единственный числовой тип.
Я не ожидаю, что формат DEC64 войдет в следующий JavaScript, поскольку это фундаментальное изменение.
Зн Теги: #математика #программирование #JavaScript #ИТ-стандарты #системы счисления

-
Когда Надоедливые Программы Не Исчезнут
19 Oct, 24 -
Pintask — Программируемый Трекер Задач
19 Oct, 24


