Это продолжение статьи Часть №1. Введение в складной биокомпьютер.
От белков к РНК .
Здесь мы опишем ковалентные и водородные связи математически.
Давайте посмотрим, на какие углы мы будем поворачивать, чтобы РНК свернулась.
И затронем вопрос «в чем сложностьЭ»
Первые два слайда: 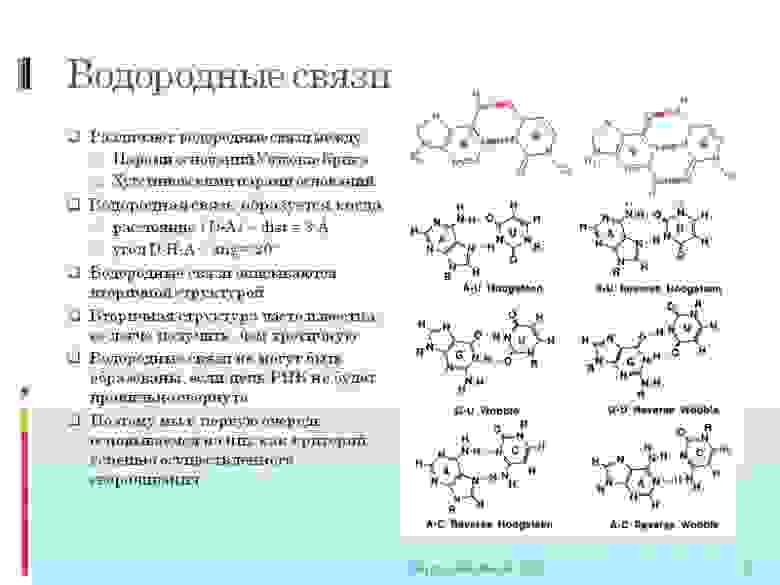

здесь вы видите более строгое определение ковалентных и водородных связей.
И как они описываются математически.
Далее для нас будет важно: 1. Подсчитать, оказались ли запрещенные ковалентные связи длиннее, чем сделать реальный оборот и вычислить десяток водородных связей.
Поэтому это делается только тогда, когда по всем остальным критериям нас устраивает найденное состояние.
Предположим, что существует просто функция GetFullCoвалентнаяБонд(), которая сообщает нам, существует ли хотя бы одна запрещенная ковалентная связь.
Если есть, продолжаем считать дальше и не учитываем такие состояния.
Хотя сравнительно в игре FoldIt быстро просчитываются коллизии и эти состояния исключаются из «плохих».
В этом есть некоторый смысл.
Но увы у меня нет алгоритма как это сделать нормально, в общем без этого пока.
2. Важно, чтобы между молекулами образовывались сразу две или три (в зависимости от типа) водородные связи.
Дальше мы будем говорить в контексте «между нуклеотидами образовалась водородная связь» — это значит, что образовались все две/три связи.
3. Сначала я очень переживал, что могут быть нестандартные водородные связи.
Те.
не так, как в ДНК есть только G с Ц и А с Т (а в РНК с U).
Могут быть разные сюрпризы.
Например, G c U, а также тройные связи А с двумя U одновременно.
4. Повторю еще раз, потому что это важно – водородная связь образуется, когда определенные атомы находятся на расстоянии <3 angstroms from each other and at a certain angle of <20 degrees. All atomic coordinates are calculated in angstroms. And there is a function ScoreGroup(int N1, int N2), where two numbers of nucleotides (molecules) in the chain are supplied, and we get an answer to how close they are to create all the necessary hydrogen bonds. The important thing here is that the answer is not just yes/no, but as a function of getting closer to “yes”.
We will discuss what exactly this function is in subsequent articles. Теперь как нам повернуть цепь.
Начнем с поворотов всего одного нуклеотида: 
Цепь поворачивается только за счет поворота на 9 углов скручивания.
По-другому он двигаться не может – это запрещено биологией (энергетикой).
6 углов входят в так называемую основную цепочку, которая на картинках в предыдущей статье показана сплошной линией.
Здесь они обозначены греческими буквами, начинающимися с альфа.
Еще три угла в боковой цепи сильно зависят друг от друга, т.е.
вращать их самостоятельно нельзя - поэтому в дальнейшем мы будем называть его углом номер 7 - но на самом деле будет комбинация из трех углов.
Боковая цепь является радикалом, т.е.
то, что собственно отличает нуклеотиды а, и, с, г – и основная цепь (12 атомов из 28-33) одна и та же.
Если у нас есть только один нуклеотид, то ясно, что мы можем вращаться на 6 углов практически без ограничений.
А по 7-му запретов очень мало.
Ничто не мешает. Если цепочка из 2-х нуклеотидов уже есть, то появляются запреты – атомы одного нуклеотида могут сталкиваться с атомами другого.
Но так как связка не большая (возьмите бусины - два соседних шарика вряд ли столкнутся друг с другом при вращении - длина нити между ними мала) - запретов тоже не так много.
А вот если брать 6 и более, запретов может быть очень много.
А вот поворот одного угла на 0,1 градус может позволить поворот на другой угол, например, образовать водородную связь, а без этого не получится.
В чем сложность? Просчитать все комбинации, скажем, за день можно только для цепочки из 2-3 нуклеотидов, для 4 уже уходит неделя или месяц, а то и годы :) Но не все ракурсы так коррелируют друг с другом.
Есть такие, которые мало влияют друг на друга.
Но никто не знает, какие они в данном случае.
Но невозможно шаг за шагом взять и задать нужные углы, поэтому я хочу разработать итерационную процедуру, чтобы шаг за шагом получать все лучшее и лучшее состояние.
Но я провел этот эксперимент. Я взял всего 3 нуклеотида (биологическое вырожденное состояние).
И мы сделали ходы в начале первого нуклеотида, нашли лучшее состояние, потом зафиксировали лучшие состояния второго, потом третьего (одна итерация - просчет, скажем, 1500+1500+1500 оборотов) зафиксировали лучшее.
.
и так далее.
Алгоритм в конечном итоге находит такое состояние с оценкой -9,41. Если мы сделаем это, мы повернем первый нуклеотид на 1500 вращений, затем для каждого из 1500 вариантов повернём второй на 1500, затем для комбинации первого и второго (1500*1500 вариантов) повернём третий на 1500 вращений.
варианты.
Мы получим действительно полный перебор примерно из 3 миллиардов вариантов и получим лучшее состояние -13,87. Но путь к полному перебору закрыт, и хотелось бы свести его к варианту локальной аппроксимации (первый вариант).
О том, как это сделать, мы поговорим в следующей части.
Для более глубокого понимания приведу две ссылки: 1. О деталях эксперимента, описанных выше 2. О свободе колебаний нуклеотидов в спирали РНК , хорошо видно, что законы максимально нелинейны и простой логики не существует. Теги: #складывание белка #складывание РНК #теория игр #кибернетика #Алгоритмы

-
«Гонки Роботов» В Уральском Федеральном
19 Oct, 24


