В 19 веке появились интересные инструменты для умножения, построенные на основе теоремы Слонимского.
Это «Снаряд умножения» Слонимского и такты Иоффе.
Настоящая статья посвящена второму из них, предложенному в 1881 году Гиршем Залмановичем Иоффе (вариант – Иоффе).
Материалов по этому инструменту в Рунете очень мало, однако, мне кажется, мне удалось восстановить их внешний вид. В любом случае, версия, которую я прикрепил ниже, близка к оригиналу и пригодна для использования по назначению.
Цель написания этой статьи
Эта статья для тех, кто, как и я, интересуется историей компьютерных технологий.Когда я написал статью [3] По поводу принципа построения таблицы Слонимского и использования ее для умножения у меня глаза затуманились и я не обратил должного внимания, так сказать, на материальную часть.
К тому же у меня на тот момент не было необходимых зацепок для восстановления внешнего вида брусков.
Поэтому, когда меня спросили о практической стороне вопроса, и у меня были на этот счет некоторые подсказки, я решил восстановить внешний вид брусков Иоффе и написать о них статью.
Почему местом для статьи был выбран Giktimes?
Статья посвящена, хотя и древней, компьютерным технологиям.Следовательно, по тематике он подходит Хабру, а хаб «История ИТ» находится, как известно, на Гиктаймсе.
Гиктаймс хорошо индексируется, и я хочу, чтобы всем, кто интересуется этим инструментом подсчета, было легко найти информацию о нем.
Назначение и описание
Иоффе-планки предназначены для быстрого составления таблицы произведений определенного заданного числа по рядам чисел от 2 до 9. Для этого на каждой грани каждого бруска записывается столбик цифр и формируется искомая таблица сложение нескольких полосок вместе в необходимом порядке.Вот что нам удалось найти в Интернете: Из источника [1]:
Счётные планки были предложены Иофе в 1881 году.Из источника [2]:В 1882 году они получили почётное упоминание на Всероссийской выставке.
Принцип работы с ними основан на теореме Слонимского.
Устройство Иоффе состояло из 70 четырехгранных брусков.
Это позволило разместить 280 столбцов Слонимской таблицы на 280 гранях.
Каждая полоса и каждый столбец были размечены, для чего использовались арабские и римские цифры и буквы латинского алфавита.
Латинские буквы и римские цифры служили для обозначения порядка, в котором нужно было расположить столбцы, чтобы получить произведение множимого на однозначный множитель.
Полученные произведения (а их столько, сколько цифр в множителе) складывались (так же, как и при использовании устройства умножения Слонимского) с помощью карандаша и бумаги.
Устройство Иофе представляло собой коробочку с десятью отсеками, пронумерованными 0, 1, 2,.Жаль, что у меня не было второго источника, когда я открыл алгоритм работы с таблицей Слонимского., 9. В каждом отсеке находилось семь четырехгранных брусков, помеченных с четырех сторон одной из цифр: 0, 1, 2 и т. д., и ниже цифры I, II и т. д. и буквы A, B, C, D соответственно с каждой стороны.
Затем по этим обозначениям располагались столбцы чисел из таблицы Слонимского, по одному столбцу на каждой грани (на 70 четырехгранных брусках ровно 280 столбцов, составляющих полную таблицу Слонимского).
Еще ниже располагаются римские цифры и те же буквы А, В, С и D. Римские цифры и буквы служили для обозначения порядка, в котором следует располагать бруски, чтобы получить произведения данного числа на однозначные множители.
Там же была картинка, иллюстрирующая принцип умножения: 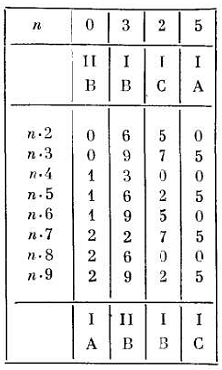
Эта картинка послужила ключом к пониманию того, что было нарисовано на решетке.
Теория
Таблица Слонимского (подробнее описана мной в статье [3] ) состоит из 280 столбцов, как доказал Слонимский, этого достаточно, чтобы сложить из них (столбцов) таблицу с произведениями любого заданного числа на ряд однозначных чисел 0.9. Для выбора нужного столбца используйте «ключ» — у Иоффе это пара «римская цифра» — «латинская буква», и цифра умножаемого числа.Иоффе использовал для ключа семь цифр, написанных римскими цифрами, и четыре буквы — т. е.
всего ключей 28. А, как известно, в десятичной системе 10 цифр.
28 * 10 = 280. Как вы можете видеть на картинке выше, в каждом столбце Иоффе написал один ключ вверху и другой ключ внизу.
Для удобства назовем их верхней и нижней клавишей.
Верхняя клавиша используется для идентификации самого столбца, а нижняя клавиша используется для выбора столбца для следующей цифры.
Кроме того, столбец вверху имеет номер — это цифра, на которую умножается, он же служит для идентификации столбца.
Алгоритм можно описать как автомат, где входной строкой является число, подлежащее умножению, читаемое справа налево (от младшего к старшему разряду), а состоянием является ключ предыдущего столбца.
На каждом этапе нам необходимо найти столбец, верхний ключ которого равен нижнему ключу предыдущего столбца, а номер которого является следующей входной цифрой.
Начальное состояние – ключ И-А, конечное состояние – тоже И-А, при условии, что номер прочитан полностью.
Чтобы избежать сюрпризов, добавьте к числу ведущий ноль.
Упражняться
Теперь проделайте то же самое с пальцами и брусьями.Гирш Залманович сгруппировал столбики по 4 по краям своих брусков, а сами брусья - по 7 в коробах.
Вышло 10 коробок.
Нетрудно догадаться, что номер ячейки должен одновременно совпадать с количеством всех столбцов в ней.
Столбики в коробочках могут иметь 7 цифр – очевидно, в этом и заключается значение римской цифры.
Далее 4 буквы, как следует из описания, обозначают четыре грани бруска.
На картинке из источника [2] изображена сложенная таблица умножения числа 325 на строку 2.9. Как я и советовал, для профилактики номеру присваивается ведущий ноль.
Повторю картинку, чтобы не пришлось листать: 
Давайте посмотрим в обратном порядке: нам необходимо последовательно найти столбцы для чисел 5, 2, 3, 0.
Начнем с состояния I-A.
Идти:
Берем блок I из коробки 5 и кладем стороной А.
Читаем его нижний ключ: I-C. Наш психический автомат переходит в состояние I-C. Берем из коробки 2-й блок I и кладем его слева от предыдущего стороной С.
Читаем его нижний ключ: I-B. Берем блок I из ящика 3 и кладем его стороной Б.
Читаем его нижний ключ: II-Б.
Берем блок II из коробки 0 и кладем его стороной Б.
Числа у нас закончились, поэтому проверяем нижний ключ последнего блока: I-A, что нам и нужно было доказать.
Приложение:
→ Разработки всех штанг PDF В прикреплённом файле каждые четыре столбца — это развитие одного такта.В горизонтальных группах на одну коробку приходится семь планок.
Литература:
1. Iofe подсчет баров Апокин И.А.
, Майстров Л.
Е.
«История вычислительной техники».
М.
: Наука, 1990. – С.
112-116. 2. Апокин И.
А.
, Майстров Л.
Е.
«Развитие компьютеров».
М.
: Наука, 1974. - С.
98-99. 3. Инструмент умножения на основе теоремы Слонимского Зениччик, Хабр, 2014 :) Теги: #математика #история информационных технологий

-
Дендримеры
19 Oct, 24 -
Домен Google.com Куплен За Одну Минуту
19 Oct, 24 -
Зачем Козе Гармошка? Опус О Сафари
19 Oct, 24 -
Наши Елки
19 Oct, 24


