Хотелось бы подробнее разобрать проблему из публикации «Олимпиады по программированию среди школьников» , а также покажем, что оно действительно нетривиально.
Хотя результирующая программа состоит из трёх заданий и двух сравнений, прийти к такому результату не так-то просто, особенно если под рукой нет справочника по аналитической геометрии.

Итак, сразу договоримся, что никаких округлений и ошибок, связанных с представлением чисел с плавающей запятой, у нас не будет. Мы будем работать исключительно с целочисленными переменными; для этого мы прибегнем к очевидным уловкам.
Хотя на самом деле программирования будет мало и много математики.
В данной работе использованы справочные материалы по университетской математике, а точнее один абзац из главы «Основы линейной алгебры и аналитической геометрии» [1].
Для начала напомню текст задачи:
Простуженный Петя лежал в постели, как вдруг кто-то открыл дверь.Ну нельзя подходить к этой проблеме «в лоб», анализ в указанной теме тоже особо ничего не «разжевывает».Пете лень было вставать, и он посмотрел в зеркало, чтобы увидеть, кто пришел.
Координаты вошедшего известны (его можно считать материальной точкой), необходимо выяснить, сможет ли Петя увидеть отражение вошедшего в зеркале.
Зеркало имеет форму круга с центром в начале координат и расположено в плоскости ax+by+cz=0. Петю также можно считать материальной точкой.
Гарантируется, что Петя и незнакомец не лежат в плоскости зеркала и что Петя всегда видит отражающую сторону зеркала.
Если изображение попадает на границу зеркала, то Петя видит входящего человека.
Поскольку материальными точками можно считать и Петю, и вошедшего, то Петя может видеть отражение вошедшего как через вошедшего, так и через собственное отражение.
Поэтому я предлагаю упростить задачу и решить ее для двумерного пространства, а затем по аналогии перейти к трехмерному пространству.
Можно, конечно, рассмотреть и одномерный вариант, но смысла в нем мало, потому что зеркало превращается в точку и Петр увидит входящего человека только тогда, когда он окажется по одну сторону зеркала, т.е.
их координаты имеют одинаковый знак.
Давайте нарисуем иллюстрацию проблемы: 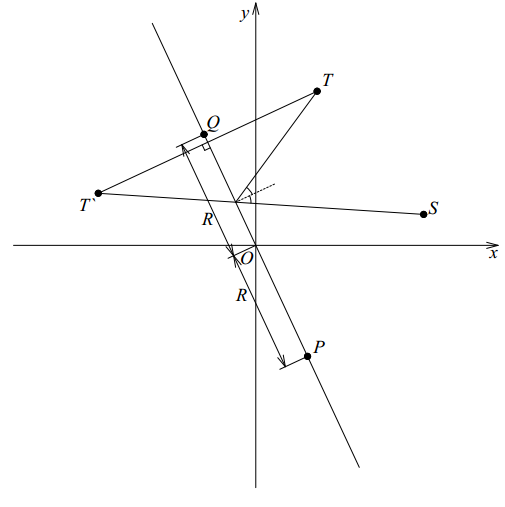
Обозначим Петю точкой С , точка зрения незнакомца Т , зеркало - прямой сегмент 
Исходные данные: р — радиус зеркала, коэффициенты А И Б ; 
— координаты входящего; 
— Координаты Питера.
Алгоритм решения следующий:
— Через точку Т провести прямую линию перпендикулярно ПК ;
— Отмечаем точку на этой линии Т` симметричная точка Т относительно ПК - это будет изображение входящего человека, которое увидит (или не увидит) Петя;
- Давайте сделаем прямой СТ` ;
— Найдем точку пересечения ПК И СТ` ;
— Проверим, принадлежит ли данная точка отрезку ПК
Итак, уравнение прямой, проходящей через точку Т перпендикуляр 
следующее: 
или 

Точка пересечения ТТ` И ПК является решением системы уравнений: 
Умножим уравнения на А И Б соответственно, и складываем: 



Найдена точка 
— проекция точки Т напрямую ПК
Определим координаты точки Т` : 

Два шага позади.
Найдем уравнение прямой СТ` : 
или 
Подставим выражения для координат Т` : 
Перейдем к целочисленному исчислению — умножим уравнение на 
: 
Пришло время представить замену: 
тогда уравнение СТ` принимает форму: 
Точка пересечения ПК И СТ` является решением системы: 




И наконец, расстояние от центра координат до найденной точки: 
Отходим от радикалов: 
Теперь, если найдут Р' будет не больше указанного р , то наш несчастный Петр все равно увидит входящего незнакомца.
В сравнении 
Умножим обе части неравенства на заведомо положительный множитель (так как это четная степень) 
те.
нас интересует истинность выражения 
Почему я так подробно все это описываю? Просто чтобы показать, какой объем работы должен проделать участник олимпиады для решения этой задачи, а ведь все эти формулы для перпендикулярных прямых не включены в школьный курс математики, участник должен сам дойти до них логическим путем? Причем на это задание ему давали в среднем 30 минут. Так что проблема фактически еще не решена.
Во-первых, то же самое нужно сделать и для трехмерного пространства, что еще более трудоемко, а во-вторых, не учитывается, находятся ли мальчик и его гость по одну сторону зеркала.
Что ж, нам не грозит нехватка времени, так что продолжим.
Разберемся с «зазеркальем».
У меня есть такое решение (хотя оно тоже не сразу пришло в голову, сначала я думал о переходе в систему координат, связанную с прямой линией зеркала, но есть "некрасивые" тригонометрические функции) - через точки С И Т провести прямые линии, параллельные данной 
.
Параллельные линии имеют несколько коэффициентов при Икс И й , т.е.

, разница только в бесплатном сроке.
Не будем ничего выдумывать и возьмем эти коэффициенты равными заданным А И Б .
Тогда уравнение прямой, проходящей через точку С параллельный ПК имеет форму: 
или 
Здесь в зависимости от знака свободного члена 
прямая будет находиться по ту или иную сторону от данной.
Аналогично для линии, проходящей через Т : 
Сделаем следующее: найдем стоимость продукта 
и сравните с нулем: если больше нуля, то точки расположены по одну сторону линии, если меньше, то по разные стороны и Петя точно не увидит своего гостя, а промежуточный ноль тоже удовлетворяет, потому что в этом случае хотя бы одна из точек лежит на данной прямой.
И напоследок приведу текст программы для трехмерного мира, т.е.
для начального условия задачи: источник
Теги: #возмущение #математика #олимпиадные задачи #программирование #математикаpackage ru.andrewn; import static java.lang.System.out; public class Program {

-
Немного О Миграции Ит-Специалистов
19 Oct, 24 -
Сравнение Анимации Gif, Webp, Apng, Bpg
19 Oct, 24


