Привет, Хабр! Решил предаться графомании и поделиться результатом развлечений минувших выходных (только эти выходные прошли уже давно и статья писалась гораздо дольше, чем развлечения.
Как говорится, время для дела - время для удовольствия) .
Я расскажу о так называемых алгоритмах расщепления (в частности, алгоритме DPLL), о теореме и числах Ван дер Вардена, а в конце статьи мы напишем свой алгоритм расщепления и за полчаса расчетов мы докажет, что число w(2; 5 ) равно 178 (на расчеты у первооткрывателей 1978 года ушло более 8 дней).
Алгоритм разделения
Это достаточно общий алгоритм, решающий следующую задачу: существует некоторое конечное множество S и мы хотим разделить его на два подмножества A и B, обладающие определенными свойствами, или определить, что множество S невозможно разделить требуемым образом.Делается это следующим образом: на каждом шаге создаются и поддерживаются 3 непересекающихся подмножества A, B, C, которые полностью покрывают множество S, где C — множество тех элементов, которые мы еще не распределили между A и B. Изначально, C = S, а A и B пусты.
На каждой итерации из множества C случайным образом выбирается элемент a, который можно поместить либо в набор A, либо в набор B. Фактически мы делаем и то, и другое, а затем рекурсивно обрабатываем обе возможности.
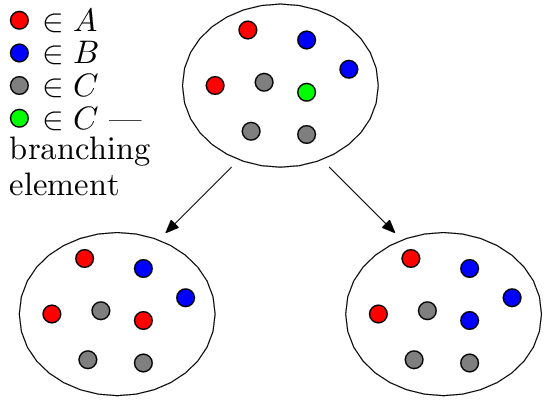
В результате получается дерево расщепления, листья которого содержат все возможные деления множества S на A и B, а множество C пусто.
Теперь нам просто нужно проверить все листья, что интересующие нас свойства удовлетворяются.
«Извините!», — скажете вы, — «чем это лучше, чем очевидный поиск 2-х |С| параметры? А все дело в разрезах, которые очень удобно добавлять в скелет предложенного выше алгоритма! Отключенный список:
- Если частично построенные А и Б не подходят — откат
- Перемещение элемента из S в A или B может привести к перемещению других элементов из S в A или B.
- Правильный выбор элемента a из S на каждом шаге позволяет существенно уменьшить размер дерева поиска.
Хотя сложность алгоритма в худшем случае все равно остается экспоненциальной.
Общий алгоритм расщепления и все предлагаемые разрезы удобно объяснить на примере классического алгоритма DPLL.
Алгоритм ДПЛЛ
Алгоритм Дэвиса – Патнэма – Логемана – Лавленда (DPLL) была разработана в 1962 году для определения выполнимости булевых формул, записанных в конъюнктивной нормальной форме, т.е.для решения задачи SAT. Алгоритм оказался настолько эффективным, что более 50 лет спустя он стал основой для самых эффективных решателей SAT. Давайте подробнее рассмотрим, что делает алгоритм DPLL. Он принимает логическую формулу и пытается разделить все переменные в ней на два набора A и B, где A — это набор всех переменных, которые оцениваются как истина, а B — это набор всех переменных, которые оцениваются как ложь.
На каждом шаге каким-то образом выбирается переменная, которой еще не присвоено значение (назовем такие переменные бесплатно ) и ей присваивается значение true (эта переменная вводится в набор A).
После этого решается полученная упрощенная задача.
Если оно выполнимо, то выполнима и исходная формула.
В противном случае выбранной переменной присваивается значение false (оно вводится в B) и задача решается по новой упрощенной формуле.
Если оно выполнимо, то выполнима и исходная формула.
В противном случае, увы, исходную формулу реализовать невозможно.
После каждого присваивания формула дополнительно упрощается с использованием следующих двух правил:
- Распространение единицы.
Если в любом дизъюнкте осталась ровно одна переменная, то ей нужно присвоить такое значение, чтобы дизъюнкт в конечном итоге стал истинным (перейти к А или Б в зависимости от того, есть отрицание или нет).
- Чисто буквальное устранение.
Если какая-либо переменная включается в формулу только с отрицаниями или всегда без отрицаний, то она называется чистый .
Этой переменной можно присвоить такое значение, что все ее вхождения будут иметь значение true, тем самым уменьшая количество свободных переменных.
Если после упрощения мы получим пустое предложение (все его простые союзы ложны), то текущая формула невыполнима и нам следует откатиться назад. Если свободных переменных не осталось, то формула допустима и работу алгоритма можно завершать.
Также возможно завершить работу алгоритма, если не осталось ни одного пункта — неиспользуемые свободные переменные могут быть назначены произвольно.
Небольшой C-подобный псевдокод, поясняющий, что происходит:
Теги: #алгоритмы расщепления #DPLL #алгоритм DPLL #SAT #теорема Ван дер Вардена #числа Ван дер Вардена #программирование #Алгоритмы #математикаbool DPLL( eq F, set A, set B, set C ) {

-
Советы Surefire Для Более Быстрой Загрузки
19 Oct, 24 -
Биохимия
19 Oct, 24 -
Фаерфокс 3.5.1
19 Oct, 24 -
3 Легендарных Харизматика
19 Oct, 24 -
Пикник С Инвесторами: Итоги
19 Oct, 24 -
Google Покажет Пробки
19 Oct, 24


