Сегодня мы рассмотрим алгоритм TILT (Transform Invariant Low Rank Texture) и его многочисленные методы применения в области компьютерного зрения.
Статья будет носить несколько обзорный характер, без углубления в математические дебри.
Идея алгоритма, можно сказать, выросла из конкурса Премия Netflix , что по сути является задачей коллаборативной фильтрации, где у нас есть матрица пользователей и их рейтингов: матрица разреженная, элементов в ней нет, а также может быть шум, и для каждого фильма мы нужно предугадать, какую оценку ему поставит каждый пользователь, т.е.
заполняем матрицу.
Изображение – это тоже матрица! Мы будем использовать определение ранг матрицы
Ранг системы строк (столбцов) матрицы A с m строками и n столбцами — это максимальное число линейно независимых строк (столбцов).А какое изображение будет иметь низкий ранг? Например, изображение, где есть регулярные структуры:Несколько строк (столбцов) называются линейно независимыми, если ни одну из них нельзя выразить линейно через другие.
Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Как показано на картинке вверху поста, мы моделируем нашу исходную матрицу как матрицу низкого ранга + разреженную матрицу с шумом, т.е.
в реальности это может выглядеть примерно так:
Теперь о самом алгоритме TILT:
К исходной постановке задачи добавляем искажение, т.е.
восстанавливаем не только матрицу низкого ранга и зашумленную матрицу, но и геометрическое искажение (например, вращение, аффинное преобразование, проективное преобразование), минимизирующее ранг матрицы.
.
Мы определим наше преобразование как матрицу гомографии, хотя можно определить и более сложное преобразование.
Но на практике они не минимизируют напрямую ранг матрицы, а берут ядерная норма , а для матрицы с шумом берется норма L1, я так понимаю это делается для регуляризации, т.е.
чтобы матрица была разреженной.
Постановка задачи минимизации:
Затем алгоритм итеративно сходится к оптимальному решению, используя методы оптимизации, как показано в видео:
Небольшой бонусный пример: уменьшение размерности матрицы с помощью SVD:
Берется изображение с регулярной структурой и в нем делается прямоугольное отверстие (цвет пикселей выставляется на 0)
5-й ранг 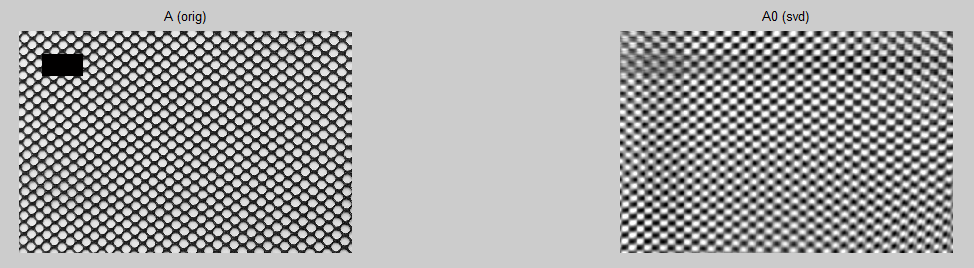
15 место 
100-е место 
Код кл, ясно
к = 100; % классифицировать
% A — матрица mxn, которую мы хотим разложить.
A = im2double(rgb2gray(imread('low_rank_img.jpg')))';
размер = размер (А)
%сделать черную дыру
А(100:100+sz(1)/8,100:100+sz(2)/10)=0;
kmax= min(размер(A));
если (к> кмакс)
к= кмах;
конец
тик
% Вычислить SVD A напрямую
[u0, S0, V0] = svd(A,'econ');
A0 = U0(:,1:k) * S0(1:k,1:k) * V0(:,1:k)';
ранг(A0)%тест, если ранг = k
содержание
display(['Ошибка SVD: ' num2str(norm(A(:)-A0(:)) /normal(A(:)))])
очистить U0 S0 V0 Теперь перейдем к самому интересному, а именно практическому применению:
Автоматическая калибровка искажений объектива:
Дополненная реальность:
Автоматический поворот текста, знаков и штрих-кодов:
И да, не только картинки с повторяющейся структурой имеют низкий ранг, но и симметрия снижает ранг! Также стоит отметить, что если у человека на одном глазу повязка (человек-пират) или его челка зачесана набок, это не помешает алгоритму «найти симметрию», ведь мы помним, что алгоритм моделирует и шум.
.
Автоматический поворот лиц, коз и любых объектов с симметрией:
Автоповорот номерного знака (небольшой привет недавним постам про распознавание номеров от ЗлодейБаал изображения сделаны отсюда ):
Другая область, в которой может быть использован этот алгоритм, — это задача живопись , но польза сомнительна, ведь нужна штатная структура и детали будут удалены.
Действительно ли алгоритм так хорош? ?
Не совсем.
Сходимость алгоритма к правильному решению зависит от инициализации, вот пара негативных примеров:
Что дальше?
Ссылка на исходный код в Matlab: Код НАКЛОНА
Ссылка на код C++ из Смородов : TILT-Cpp-порт И Самокалибровка
Ссылки на публикации: TILT: преобразование инвариантных текстур низкого ранга
Ссылки на лекции: Низкоранговое моделирование | Поиск низкоразмерных структур в многомерных данных, Йи Ма, Microsoft
Теги: #Обработка изображений #линейная алгебра #методы оптимизации #компьютерное зрение #OpenCV #Обработка изображений
-
Виртуальное Будущее Университетов
19 Oct, 24 -
Заметки О Жизни В Сша
19 Oct, 24 -
Фильм Будет Платить Создателям За Видео
19 Oct, 24 -
Пробка Пиявки Для Экономных
19 Oct, 24 -
Тс50 2009 Г.
19 Oct, 24 -
Как Интегрировать Zimbra С Dlp-Системой?
19 Oct, 24


