В этой статье описывается метод разворачивания этикетки в шести точках.
Этот метод является обратной задачей рендеринга, т.е.
по ключевым точкам определяется геометрия бутылки и рассчитывается исходная плоскость изображения.
Все манипуляции производятся с использованием библиотеки OpenCV. Добро пожаловать коту!
Прежде всего, давайте разберемся, что такое цилиндрическая дисторсия.
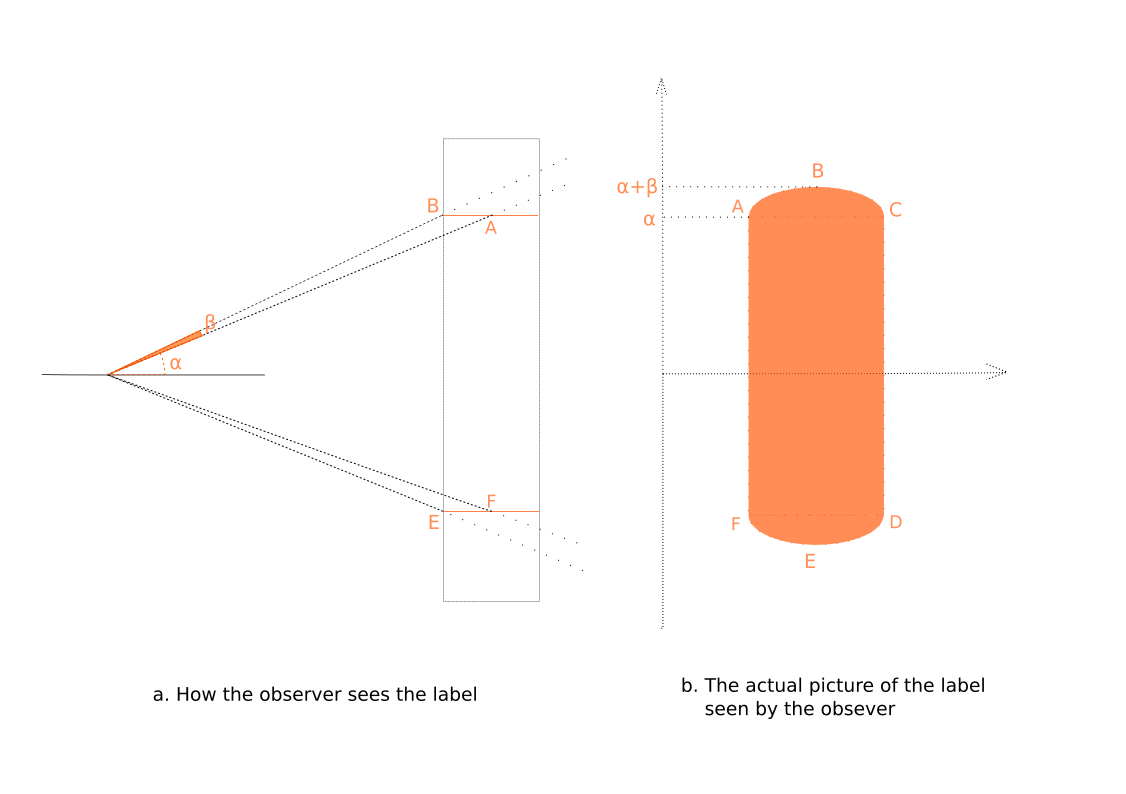
Прямоугольная этикетка, приклеенная на цилиндр, имеет характерную бочкообразную форму (б на схеме выше).
Кривая АВС в данном случае, в достаточно хорошем приближении, представляет собой эллипс, поскольку мы видим окружность (сечение цилиндра) под углом.
Множество горизонтальных линий этикетки аналогичным образом преобразуются на фотографии в множество эллипсов.
Самое интересное, что для разворачивания метки достаточно указать 6 маркеров (ABCDEF): 
И используя их, постройте полную сетку поверхности: 
Учитывая сетку поверхности, мы можем вращать каждую плитку индивидуально, чтобы получить исходную поверхность: 
Код библиотеки доступен на Github. .
Удобство этого метода состоит в том, что входными параметрами обратного преобразования являются визуально определяемые характеристики этикетки (углы, верхняя и нижняя точки), что позволяет полностью автоматизировать процесс.
Следующая часть посвящена идентификации маркеров.
Рабочий код доступен лишь частично в ветка на Github , потому что реально работающее решение покрыто хаками и шаманством, поэтому моя совесть просто не позволяет мне выложить подобное на GitHub. Шаг первый – преобразуем изображение в черно-белое.
Затем вам нужно получить контур бутылки с этикеткой.
Для этого мы используем трансформация Собеля .
Короче говоря, этот фильтр сначала размывает изображение, а затем вычитает его из оригинала.
В результате однородные области остаются темными, а края (вариации) — светлыми.

Следующее, что вам нужно сделать, это определить две наиболее заметные вертикальные линии, которые, если вам повезет, окажутся краями бутылки.
В данном случае это правда, но если сфотографировать бутылку, стоящую рядом с другими бутылками, то это уже не так.
Чтобы определить эти линии, мы используем Преобразование Хафа .
Суть методики в том, что мы берем множество линий, проходящих через весь экран, и вычисляем среднее значение пикселя (например, берем линии, идущие от верха картинки к низу).
Переносим эти значения в новую координатную плоскость и получаем что-то вроде тепловой карты.
На этой тепловой карте мы ищем две крайности — это боковые линии.
На диаграмме ниже показано, как левая линия идет к точке на новой координатной плоскости: 
С эллипсами немного сложнее, но зная, что преобразование Хафа можно применить к любым математически заданным кривым, мы снова воспользуемся этим методом, но на этот раз будем искать множество эллиптических кривых.
Но сначала нам нужно привести задачу к двумерному виду.
Зная, что бутылка центрально-симметрична, примем центральную ось за координату Y, а одну из сторон за координату X. В качестве значений на новой координатной плоскости примем набор эллипсов, построенных между центральной осью и координатой X. сторона.
Это возможно благодаря тому, что произвольная точка сбоку и центральная ось имеют только один способ соединения.
Это может быть не очень очевидно на первый взгляд, но гораздо легче понять, если обратиться к параметрической формуле эллипса:
х = а * потому что (т)
у = б * грех (т) 
Точно так же мы найдем два искомых экстремума, которые и определят два эллипса метки (кривые А-Б, Ф-Е).
Теперь, когда у нас есть все необходимые параметры метки (боковые кривые, а также верхний и нижний эллипсы), мы можем применить алгоритм из первой части статьи и выполнить обратное преобразование.
Что можно улучшить.
Во-первых, алгоритм не учитывает искажение перспективы самого эллипса, в результате чего боковые фрагменты метки растягиваются немного больше, чем следовало бы.
Чтобы внести коррекцию, нужно знать реальный угол обзора камеры или хотя бы использовать наиболее типичный для телефона (можно подобрать опытным путем).
Во-вторых, преобразование Хафа работает довольно нестабильно в сложных условиях — например, когда в кадр попадают близлежащие бутылки, и края интересующей бутылки могут определяться неправильно.
В-третьих, если метка не прямоугольной формы (например, эллиптическая), то маркеры будут определены неправильно, и трансформация только сильнее исказит изображение.
На практике гораздо интереснее использовать нейронную сеть для определения маркеров, поскольку ее можно обучить на сложных примерах так, что, как минимум, алгоритм не выполняет преобразование, если маркеры не могут быть определены.
Но пока я не пробовал использовать нейрон для этой задачи, так что, возможно, это будет тема отдельной статьи :) Теги: #Машинное обучение #python #Обработка изображений #python opencv
-
Надежные Оригинальные Картриджи Brother
19 Oct, 24 -
Как Исправить Ошибки, Связанные Со Скоростью
19 Oct, 24 -
Фстэк: Требования К Межсетевым Экранам - 2
19 Oct, 24


