Привет, меня зовут Женя.
Сегодня я расскажу вам, что такое квантование вложений, какие методы квантования существуют и как с их помощью мы в Яндекс.
Дзен смогли сократить использование памяти, скорость записи и сетевой трафик в четыре раза.
Будет совсем немного математики, умеренные размышления о машинном обучении, highload и big data и много красочных картинок.
Что такое вложения?
Эbedding — это числовой вектор, который каким-то образом (вообще непонятным глазу) характеризует интересы или контент пользователя.Например, вложения могут быть такими.

Каждый пользователь и карта могут иметь несколько вложений разных типов.
В основном используются два типа вложений.
Содержание — на основе содержания карточки в ленте (заголовок, текст, картинка, тема).
Две статьи с одинаковым заголовком о самолетах будут иметь схожие вложения.
Совместный — на основе оценок похожих пользователей и карточек (лайки, дизлайки, клики, блокировки).
Две статьи будут иметь одинаковые вставки, если статьи нравятся пользователям со схожими интересами.

Зачем нужны вложения?
Расскажу поверхностно (столько, сколько необходимо для этого поста), потому что о матричной факторизации и принципах работы рекомендательных систем уже написано много отличных статей.Например:
- здесь Павел Пархоменко пархоменкопа ясно и лаконично объяснил смысл алгоритма АЛС;
- здесь Михаил Ройзнер М.
Ройзнер подробно рассказал о структуре рекомендательных систем;
- здесь Никита Мокров Тисмони подробно описывает различные методы матричной факторизации.
Его задача — найти материалы, которые с наибольшей вероятностью будут интересны пользователю.
Например, так выглядит мой канал
Для выбора таких карт мы прогнозируем рейтинг пользователя для всех карт и выбираем карты с лучшим рейтингом.
Для решения этой задачи используется матрица оценок (заимствована из почта Паша): 
В нем расположены пользователи в строках, карточки в столбцах, а на пересечении оценки, которые пользователи поставили карточкам.
Мы не знаем большинства оценок — нам нужно их предсказать.
Настоящая рейтинговая матрица Zen весила бы более 100 ТБ.
Такую матрицу сложно уместить на диске одной машины, не говоря уже о памяти.
Но поскольку матрица в основном пуста, мы можем применить алгоритмы факторизации матрицы, такие как ALS (чередующиеся наименьшие квадраты), чтобы эффективно использовать ее для прогнозов.
Вместо этой тяжелой матрицы мы возьмем две другие — P и Q, которые при перемножении дадут матрицу, близкую к исходной матрице рейтингов.
P — матрица пользовательских вложений, а Q — матрица вложений карт. Выбирая длину встраивания (d), можно найти оптимальный баланс между качеством аппроксимации оценочной матрицы и ее размером.
Использовать вложения в расчетах гораздо удобнее: для построения рекомендаций для одного пользователя нам не нужны вложения других пользователей.
Вложения удобно хранить в сегментированных хранилищах ключей и значений.
Зачем их квантовать?
Мы считаем встраивания пользователей и карточек в автономном режиме, потому что некоторые встраивания дорого подсчитывать во время выполнения, а другие невозможно.У каждого пользователя и каждой карты есть несколько десятков вложений.
Каждое вложение представляет собой массив примерно из 100 чисел с плавающей запятой (float).
Соответственно, одно вложение весит около 400 Б.
Для ранжирования нам потребуется встраивание около семи миллионов карточек.
Они весят в общей сложности около 100 ГБ .
Внедрения карточек со временем мало меняются (встраивания контента изменяются только при редактировании карточки).
Просто хранить вставки карточек в базе данных невозможно, потому что для каждого запроса вам придется считывать их все в память.
Поэтому мы храним их все в памяти на каждой машине, шардируя по типам карт. Постельное белье пользователей меняется после каждого взаимодействия с лентой Zen (например, клика и даже показа карточки).
Мы подсчитываем их при потоковой обработке и сохраняем в специальном распределенном хранилище «ключ-значение» в памяти.
Для одного запроса нам необходимо прочитать из хранилища несколько десятков пользовательских внедрений (встроений пользователя, для которого мы подбираем рекомендации).
Поэтому хранить их в памяти каждой машины не обязательно, да это и невозможно — мы храним вложения примерно на 300 миллионов пользователей, а это более 10 ТБ памяти.
Встраивания пользователей хорошо сегментируются с использованием хеша из user_id. С точки зрения использования вложений архитектура времени выполнения Яндекс.
Дзен выглядит примерно так (конечно, это очень упрощенная схема).
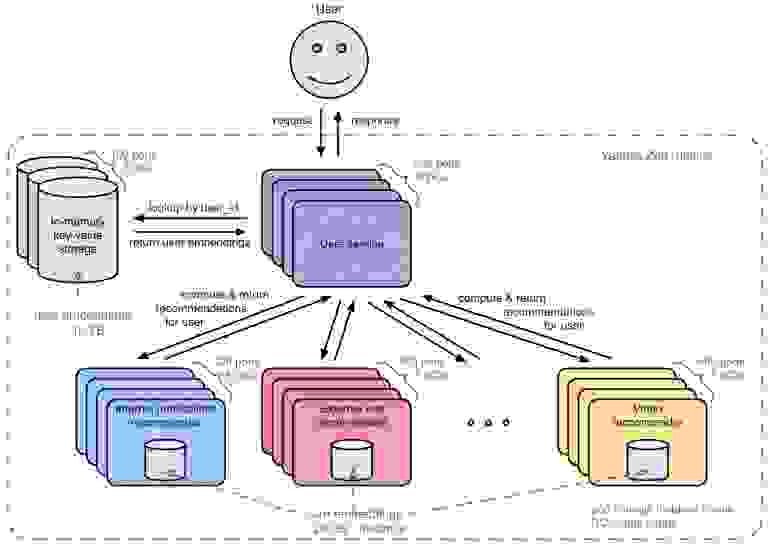
На снимке вы можете увидеть несколько узких мест.
- Пользовательские внедрения занимают много места для хранения.
10 ТБ памяти стоят немалых денег.
- Встраивание карточек съедает много памяти в экземплярах рекомендателей.
За счет большой избыточности всего имеется целых 24 ТБ памяти.
Более того, необходимость иметь встраивания всех карточек одного типа в каждом экземпляре усложняет горизонтальное масштабирование.
- Пользовательские вставки летают по сети, съедая около 300 МБ/с сетевого трафика.
- Хоть на этой картинке и не видно, но скорость записи пользовательских вложений в логи WAL на SSD (внутри хранилища) тоже является дорогим ресурсом.
Скорость записи около 300 МБ/с.
С помощью квантования можно преобразовать непрерывный диапазон значений в набор дискретных значений фиксированного размера.
Другими словами, мы преобразуем плавать (четыре байта) в байт (один байт).

Оказалось, что существуют методы квантования, которые могут сжимать наши вложения в четыре раза без существенного ухудшения качества рекомендаций.
Визуализация вложений
Во-первых, нам нужно понять, с чем мы имеем дело — внимательно посмотреть на структуру вложений.
Постельное белье можно визуализировать, например, так: 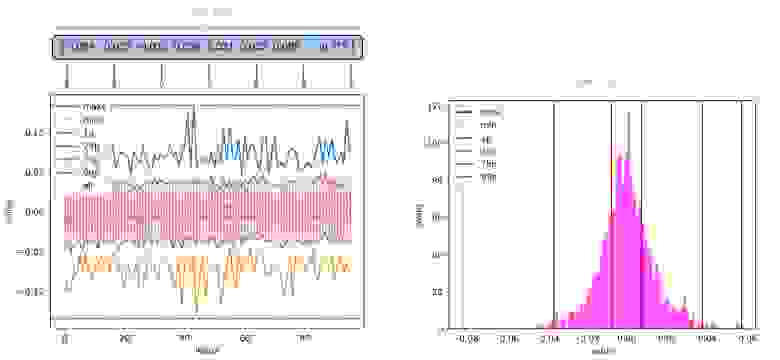
На левом рисунке по оси X расположены индексы, а по оси Y — значения вложений по этим индексам (розовые точки).
На рисунке показано уплотнение точек по всем индексам в области 0. Для удобства оценки степени уплотнения проведены линии максимального и минимального значений ( максимумы И минут ) и некоторые процентили ( 1р - первый процентиль).
На правом рисунке для наглядности представлена гистограмма значений только по 42-му индексу.
Аналогично рисуются вспомогательные линии (минимумы, максимумы и процентили).
Распределение по всем индексам имеет куполообразную форму.
Иногда это выглядит нормально, но в целом это не так.
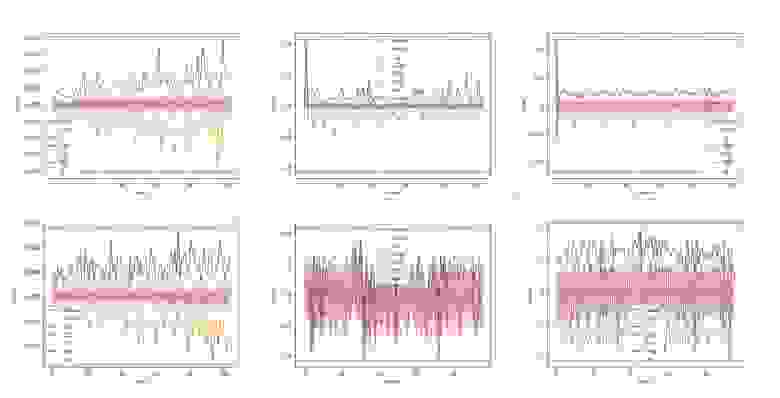
Другие типы вложений имеют сложности.
Например, разброс значений может существенно различаться от индекса к индексу.
Купол может быть широким или узким.
Вершина купола не всегда находится на нуле, а также может существенно меняться от индекса к индексу.
В основном мы изучили три алгоритма квантования, и сейчас я вам о них расскажу.
Мы придумывали имена, как могли.
Минимальное-максное квантование
Наверное, первая идея, которая может прийти в голову, — вырезать интервал между минимальным и максимальным значениями и разделить его на равные участки.
Для каждого индекса преобразование будет выглядеть примерно так: 
На рисунке серые цифры между пунктирными линиями обозначают номер сегмента, в который попадает значение встраивания.
Это число является квантованным значением.
На самом деле сегментов будет 256, а не 12.
Формально преобразование можно выразить следующим образом: 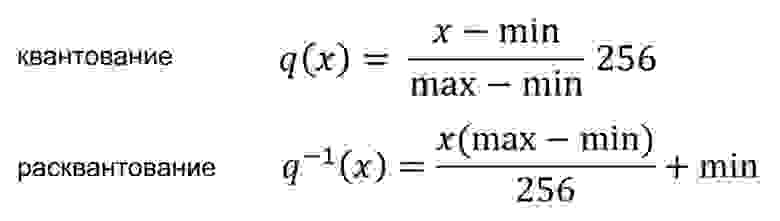
Оба преобразования представляют собой простые линейные смещения по каждому индексу внедрения.
Для всех значений индекса мин И Макс могут существенно отличаться (как видно из приведенных выше распределений).
Следовательно, для каждого типа встраивания нам необходимо хранить два вектора размера д с минимумами и максимумами (около 800 Б для каждого типа встраивания).
Этот подход прост в реализации и не требует много ресурсов для преобразований.
Однако есть очевидный недостаток — для некоторых типов вложений значительная часть значений попадет в пару центральных сегментов.
В этом случае мы потеряем полезную информацию о пользователе или карте.

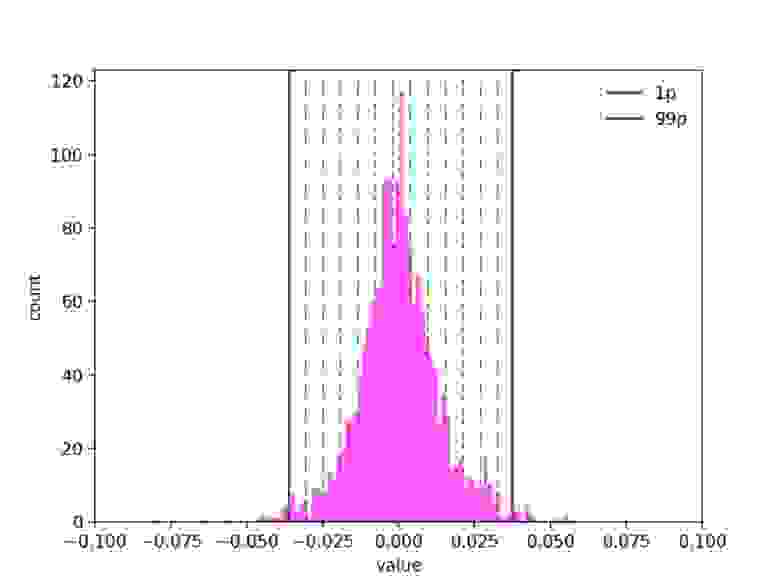
В большинстве случаев вместо минимумов и максимумов достаточно взять значения крайних процентилей, например, 1-го и 99-го.
«Экспериментальным путем мы выяснили, что наши встраивания можно обрезать аж до 5-го и 95-го процентиля без потери качества рекомендаций.
Таким образом, округляя по 1% точек в обе стороны, мы получаем существенный выигрыш: сохраняем больше информации при уплотнении вокруг нуля.
Квантование 255-квантилей
В подходе мин-макс мы пытались представить, что наше распределение близко к равномерному.Чем меньше оно похоже на равномерное, тем хуже будет работать квантование.
А что, если мы сами приведем это распределение к равномерному? Оказывается, это совсем не сложно.
Нам нужно, чтобы сегменты в разреженных областях были длиннее, а в плотных — короче.
Границы сегментов выберем так, чтобы каждый сегмент содержал равное количество значений.
Если бы мы хотели получить 100 сегментов, нам идеально подошли бы процентили.
(1, 2, .
, 99) .
Для 256 сегментов нам придется взять следующие процентили: (0,389, 0,778, .
, 99,611) .
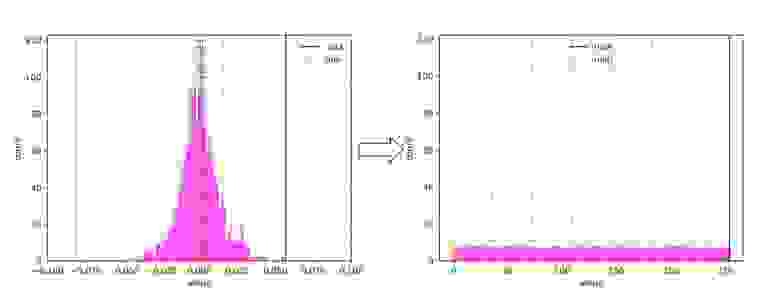
Этот алгоритм квантования сохраняет максимальное количество информации и одинаково хорошо работает с любым исходным распределением.
Это также легко реализовать:
- Предварительный расчет границ интервалов (квантили) на основе образца внедрения;
- квантование: для каждого значения встраивания находим соответствующий интервал.
Это можно сделать с помощью двоичного поиска, но на практике может оказаться, что более эффективным будет простой поиск интервалов в порядке возрастания;
- квантование: с помощью индекса сегмента восстанавливаем его центр.
Это просто одно чтение по индексу из массива.
Для каждого индекса внедрения необходимо хранить все сегменты — массив из 257 элементов.
Умножьте на 100 (размер встраивания) и 4 (байты в плавать ).
Всего ок.
100 КБ по типу встраивания.
Все еще несущественно для современных машин.
квантование с присоединенным экстремумом
Хранить дополнительные данные о встраиваемой структуре может быть неудобно.Это может быть связано, например, со сложностями в управлении версиями и синхронизацией вложений.
Либо со сложностями интеграции с другими сервисами (например, квантовать в одном сервисе, а деквантовать в другом).
В этом случае следует обратить внимание на алгоритм квантования присоединенного экстремума:
- Возьмем одно произвольное вложение.
- Найдем максимум по модулю по всем индексам — назовем его экстра .
Значения всех индексов лежат в интервале [-экстра; экстра] .
- Нарушение интервала [-экстра; экстра] на 256 равных сегментов и принять индекс сегмента как квантованную величину (как в подходе мин-макс).
- Значение extr отправляется/сохраняется вместе с встраиванием.
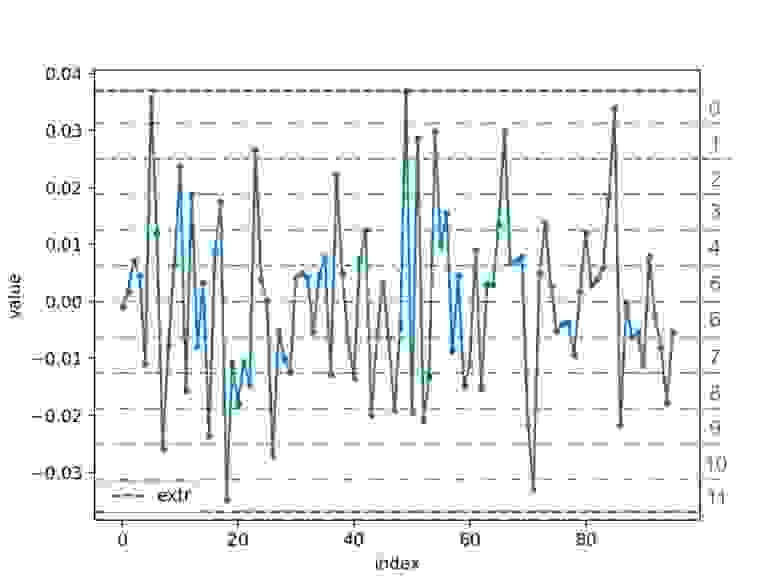
Важно отметить, что каждое вложение будет иметь свое собственное экстра в отличие от подхода min-max, где значения мин И Макс — общий для всех вложений одного типа.
Формулы квантования и деквантования легко получаются из формул min-max путем подстановки экстра И –extr вместо Макс И мин .

Допущения, которые должны быть соблюдены, чтобы этот метод квантования работал хорошо:
- распределения по индексам при встраивании примерно одинаковы (если индекс я значения попадают в интервал [–100; 100] и дальше я +1 - в интервале [–1; 1] , то почти все значения по индексу я +1 мы проиграем);
- значения встраивания по всем индексам расположены в районе 0 (если они находятся в интервале [99,9; 100,0] , то все попадут в один и тот же интервал).
Как выбрать?
При выборе метода квантования стоит учитывать:- распределение значений встраивания (для 255-квантильного квантования требования отсутствуют, для квантования с присоединенным экстремумом требования наиболее строгие);
- вычислительная мощность (255-квантильный подход может быть значительно тяжелее);
- динамика встраивания (изменения в распределениях встраивания в индексы влияют на 255-квантильное квантование больше, чем другие подходы);
- хранение дополнительных данных о вложениях (для квантования присоединенного экстремума ничего хранить не нужно).
В автономном режиме они сравнивали на основе таких критериев, как процент совпадений среди лучших карточек рекомендаций, среднеквадратическая ошибка оценки рекомендаций и т. д. Во время выполнения они сравнивали на основе ключевых показателей Яндекс.
Дзен в A/B-экспериментах.
Мы выбрали мин-максный подход с обрезкой 1-го и 99-го процентиля.
По влиянию на качество рекомендаций он существенно не отстает от 255-квантильного подхода.
Однако 255-квантиль в нашем случае совершенно неприменим для квантования вложений карточек, поскольку за один запрос пользователя нам необходимо квантовать несколько десятков тысяч таких вложений.
Чтение элемента массива по индексу для каждого индекса каждого вложения слишком затратно.
При использовании подхода «мин-макс» эта проблема решается довольно хорошо.
Чтобы вычислить скалярное произведение встраивания пользователя и встраивания карты, мы можем вообще избежать квантования встраивания карты (с присоединенным экстремумом этот трюк не работает из-за того, что каждое вложение имеет свое экстра ).
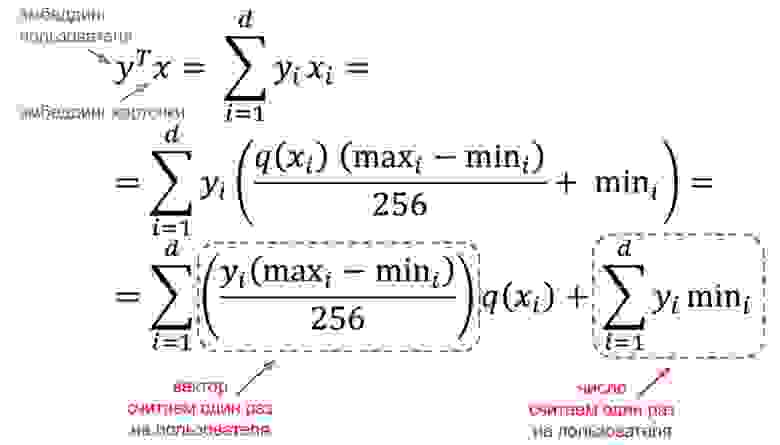
Какова прибыль?
При том же качестве рекомендаций мы сократили используемую память в четыре раза, сократили сетевой трафик к пользовательским встраиваниям в четыре раза и снизили скорость записи вложений в журналы WAL на SSD внутри нашего хранилища вложений в памяти на четыре раза.Оптимизация этих узких мест (с точки зрения потребления дорогостоящих ресурсов) позволила нам рассчитывать в четыре раза больше различных типов вложений и быстрее экспериментировать с новыми разновидностями.
Что, в свою очередь, позволит Яндекс.
Дзен более полно и глубоко понимать интересы пользователей, чтобы рассчитывать более точные персональные рекомендации.
Теги: #Машинное обучение #Высокая производительность #Большие данные #встраивания #квантование #Дзен #Команда Яндекс.
Дзен

-
Ноутбуки И Эффект Pvp!
19 Oct, 24 -
Плохая И Хорошая Кириллица
19 Oct, 24 -
Проблемы С Принятием Себя
19 Oct, 24 -
Swift Heroes 2018. Как Это Было
19 Oct, 24 -
Душ Для Любителей Rss
19 Oct, 24


