Сортировка Бисера

Сортировка бисера

Сегодня я представлю вашему вниманию симпатичный алгоритм, который хоть и был изобретен совсем недавно (11 лет назад), но «прототипом» представлял собой вычислительное устройство с трехтысячелетней историей.

Всем известно, что родоначальником счетов в Европе является счеты , которые переселились из Вавилона в Египет, оттуда в Грецию, оттуда в Рим, откуда по всей Европе.

Внешний вид и принцип работы древнего «калькулятора» настолько напоминают поведение этой «простой» сортировки, что его иногда называют «калькулятором».

Сортировка счетов "(сорт Абакус).

Алгоритм

Сортировка бисера

Предположим, нам нужно отсортировать набор натуральных чисел .

Разложим каждое число одно под другим в виде горизонтальный ряд из соответствующего количества шариков.

Теперь давайте посмотрим на все эти группировки шариков не горизонтально, а вертикально .

Давайте передвигать шарики вниз до тех пор, пока они не остановятся.

Снова переключимся на горизонтальные линии и посчитаем бисеринки в каждом ряду.

Мы получили оригинальный набор цифр, только заказанный.

Выполнение Сортировка бисера на более чем 30 языках программирования можно найти Здесь .

Хотя визуально алгоритм выглядит гораздо проще, с точки зрения программной реализации это весьма нетривиальная сортировка.

Вырожденный случай

Сортировка бисера

Это обратный упорядоченный массив .

Максимально возможное количество шариков должно будет упасть с самых высоких точек.

Ограниченная применимость Метод применим, прежде всего, к натуральные числа .

Вы также можете сортировать целые числа, но это более запутанно — отрицательные числа придется обрабатывать отдельно от положительных.

Ничто не мешает вам сортировать дробные числа, если предварительно преобразовать их в целые (например, умножить все на 10^к , отсортируйте, а затем разделите на 10^к ).

И, конечно же, таким образом можно даже сортировать строки, если каждая из них представлена как целое положительное число.

Но почему? Временная сложность У сортировки их целых 4, в зависимости от контекста, в котором рассматривается алгоритм.

Сортировка бисера

О(1)

Абстрактный корпус, сферический Сортировка бисера в вакууме.

Если представить, что все движущиеся шарики одновременно двигаются и становятся на свои места.

Это нереализуемая сложность для такой сортировки — ни в теории алгоритмов, ни на практике.

О(√n)

Рейтинг за физическая модель , где бисеринки скатываются по хорошо смазанным спицам.

Время свободного падения пропорционально квадратному корню из максимальной высоты, которая, в свою очередь, кратна н .

На)

Шарики, еще не достигшие своих мест, перемещаются вместе на одну позицию вниз за одну итерацию.

Об этой сложности уместно говорить в случае физических устройств, реализующих данный метод сортировки, аналоговых или цифровых аппаратных реализаций.

Сортировка бисера

ОПЕРАЦИОННЫЕ СИСТЕМЫ)

С – сумма элементов массива.

Каждый шар движется индивидуально, а не катит группы шаров одновременно.

Адекватная оценка сложности для реализации на языках программирования.

Трудности с памятью Оставляет желать лучшего.

Сортировка бисера рекордсмен по расточительности - стоимость дополнительной памяти во много раз превышает стоимость хранения самого массива и в среднем составляет На² ) .

Физика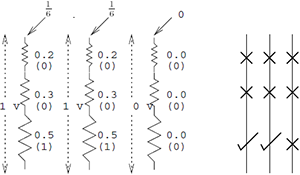

Сортировка бисера

Наличие или отсутствие шаров можно интерпретировать как аналоговое напряжение проходя через ряд электрических резисторов.

Стержни, по которым движутся шарики, являются аналогами.

электрические резисторы , напряжение в котором возрастает сверху вниз.

Не упрекайте меня за косноязычное использование терминов электротехники; В школе я получил тройку плюс четверку с минусом по физике.

Я отсылаю экспертов по электростатике на эту страницу за подробностями.

PDF-документ .

Фактически Сортировка бисера - это сорт сортировка по подсчету .

Количество шариков в каждой вертикальной дорожке — это количество элементов массива, равное или превышающее порядковый номер вертикали.

Характеристики алгоритма

Имя	сортировка бисера; Сортировка счетов
Авторы	Джошуа Дж. Аруланандам, Кристиан С. Калуд, Майкл Дж. Дайнин
Год издания	2002
Сорт	Сортировка распределения
Устойчивое развитие	Устойчивый
Сравнения	Никаких сравнений
Временная сложность	О(1)	О(√n)	На)	ОПЕРАЦИОННЫЕ СИСТЕМЫ)
Трудность с памятью	На² )