Первая часть Первая часть второй части Вторая часть второй части Что ж, господа, пора заканчивать.
В последней статье серии (название которой ломает мой, еще не до конца проснувшийся шаблон) мы поставим точку в истории этой задачи.
Несмотря на то, что в комментариях ко второй части был предложен более удобный и универсальный способ сделать это, я все равно буду использовать те инструменты, которые разработал лично мной до написания первой из статей.
Во-первых, не упускайте хорошее, а во-вторых, думаю, все понимают, что задание — это всего лишь повод нарисовать красивые рисунки в GeoGebra и выложить их на Хабр.
Ну, как говорится, поехали.
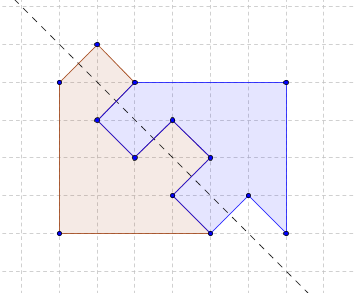
Случай 3: скользящая симметрия
Скользящая симметрия определяется следующими параметрами: осью симметрии и параллельным ей вектором сдвига.Ось симметрии, в свою очередь, определяется направлением и конкретным положением на плоскости.
Теперь я изложу ряд вытекающих друг из друга фактов, достаточно очевидных, чтобы их даже не называть леммами, а тем более доказывать.
- Ось скользящей симметрии равноудалена от границ (понятие границы мы берем без ограничений из случая параллельного переноса).
- Если взять отрезок с концами на разных границах, то ось симметрии пройдет через его середину.
- Задавая направление оси скользящей симметрии, мы автоматически распознаем ее конкретное положение.
Если обе границы состоят из одной точки, то мы также знаем вектор сдвига.
- Части, на которые фигура разделена осью, имеют равную площадь (этот факт не следует из предыдущих)
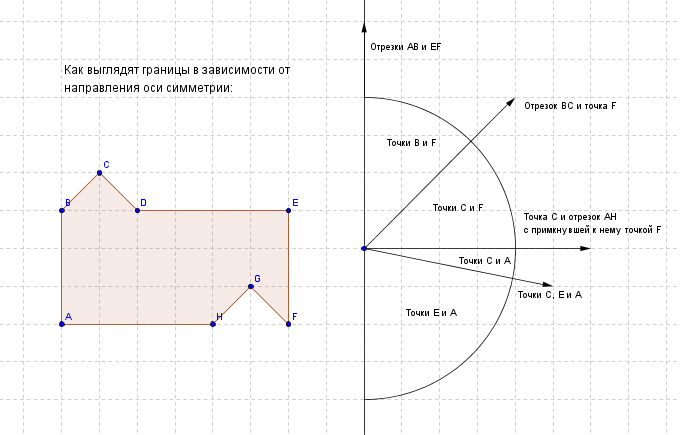
Он показывает, что для большинства направлений либо точки А и Е, либо точки В и F будут находиться на границах, а значит, ось будет проходить через «центр» фигуры (пересечение диагоналей прямоугольника ABEF).
Вторым по распространенности является случай с точками С и F, почетным третьим - с точками С и А.
В этих случаях, очевидно, ось симметрии будет проходить через середины отрезков CF и CA соответственно.
Теперь посмотрим, в каких направлениях ось разделит фигуру на две равные части.
Не вдаваясь в нудные подробности, просто скажу: но с такими.
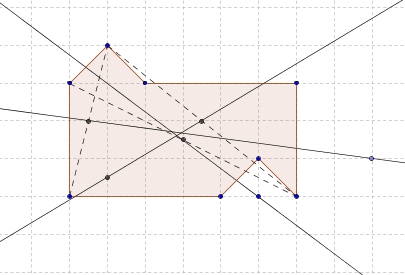
Теперь у нас есть три конкретные оси и к тому же к ним привязаны три конкретных вектора смещения — ведь границы во всех случаях состоят из одной точки.
Нетрудно показать, что для всех этих трёх скользящих симметрий существуют точки фигуры, для которых нет ни образа, ни прообраза, — что, согласно лемме 3, означает, что это плохие, непригодные для использования скользящие симметрии, которые не могут соответствовать разделение фигуры на две равные части.
Я оставляю поиск конкретных моментов читателю.
Заключение
Рисунок А 0 запрещено разрезать на две равные части.Теперь со спокойной совестью пойду пересматривать «А зори здесь тихие».
С Днем Победы, товарищи Хабровщины.
Теги: #математика #геометрия #комбинаторная геометрия #ололошечки и бугагашечки #математика

-
Учет Времени – Meteorhr
19 Oct, 24 -
Удобство Наблюдения Сверху
19 Oct, 24 -
Iso Готовит Стандарт Облачной Безопасности
19 Oct, 24


