Введение В этой статье будет обсуждаться метод распознавания рукописного ввода путем анализа всех точек плоскости и опробования всех возможных комбинаций, чтобы найти лучшее наложение контрольных точек на ранее описанные фигуры.
Позволь мне объяснить.
Почерк — это рисование определенной формы воображаемой «ручкой».
Рисование в компьютерных системах — это хранение информации обо всех пикселях графического контекста в графической памяти.
«Точка на плоскости» в математике — абстрактное понятие.
В компьютерной графике под этим понятием скрывается «пиксель».
Этот алгоритм распознавания будет анализировать предоставленный ему набор точек (пикселей) и пытаться найти в нем максимально возможную и похожую фигуру.
Фигура, в свою очередь, представляет собой кадр, содержащий только основные (контрольные) точки, делающие фигуру уникальной.
Материальная часть
В общем, суть алгоритма всем известна еще со школы.Теорема о косинусе , что является обобщенной теоремой Пифагор .
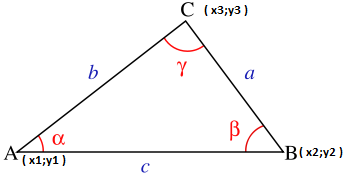
Зная координаты трех точек на плоскости и порядок их «появления» на ней, мы легко можем определить угол, описываемый этими точками (Вершиной угла является вторая точка):
Зная косинус, можно легко вычислить угол.
А(х1;у1) Б(х2;у2) С(х3;у3) расстояния между точками находятся с помощью теоремы Пифагора a^2 = b^2 + c^2 — 2*b*c*cos(АЛЬФА) потому что (АЛЬФА) = (b^+c^-a^) / 2*b*c
Среди множества точек, подаваемых на вход алгоритма, необходимо «подставить» точки в различные рамки фигур (о них выше) и выбрать лучшее решение среди найденных.
Это делается следующим образом:
На словах что-то может быть не понятно.Если эти два условия выполняются, то алгоритм принимает решение включить точку из множества точек в мыслимый кадр (при этом мы увеличиваем значение сходства с текущей анализируемой фигурой).
- Берем первую и последнюю точки рамок фигуры.
Их уже два, осталось найти третий (найти угол).
- Поиск третьего осуществляется путем перебора всех последующих точек после первой.
Решение о включении точки в предлагаемую рамку рисунка принимается на основе двух анализов:
- Попытка вставить точку в угол (как третью, заключительную) и проверить ее на соответствие значению того же угла в кадре реальной фигуры.
- Сверьте соотношение сторон полученного угла с таким же соотношением сторон угла в рамке реальной фигуры.
Если, скажем, у нас есть несколько анализируемых кадров, например, «8» и «6».
И результат алгоритма распознавания: «8» — 80%, «6» — 90%, тогда решение принимается в пользу той фигуры, кадр которой содержит больше контрольных точек, то есть в пользу восьмерки.
Процент сходства между набором точек и точками в кадре рассчитывается просто: все точки, сходящиеся с такими же точками в кадре, суммируются и находится связь.
Допустим, если в кадре N контрольных точек, а у нас M, то процент сходства равен
M / N * 100
Поэтому всё так же, но наглядно (на примере цифры «6»): 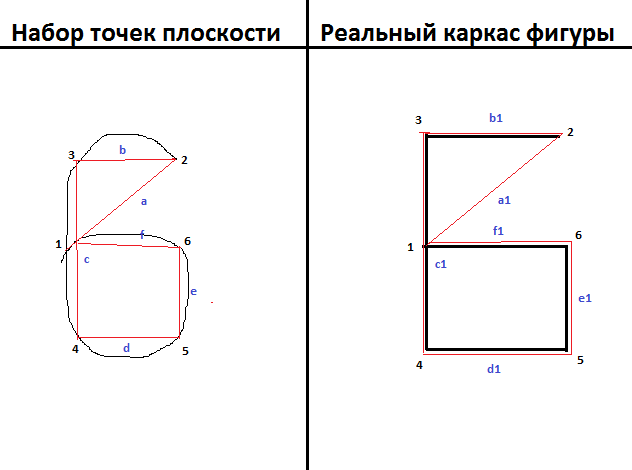
Наборы точек обозначены черным цветом, рамка, в соответствии с которой происходит анализ, – красным.
Цифрами обозначены точки углов (начиная с последней), если считать, что мы рисуем шестерку от точки «2» и заканчиваем точкой «1», то первые две точки, с которых начинается разбор кадра — «1» и «2», затем происходит поиск точки «3», чтобы ее параметры относительно образуемого ею угла совпадали с такими же параметрами в кадре.
Далее, как мы нашли точку «3», ищем точку «4» (уже опираясь на точки «2» и «3»), опять же в соответствии с реальным кадром и т.д. Буквы обозначают стороны углов.
То есть, следуя правилам алгоритма, точка из множества (точек плоскости) может войти в предложенный кадр, если (примеры):
(угол 2 ~= угол 2 в кадре) И (a/b ~= a1/b1) тогда будет включена точка «3» (угол 3 ~= угол 3 в кадре) И (b/c ~= b1/c1), тогда будет включена точка «4».На этом описание алгоритма заканчивается.и т. д.
Код
Легко сказать, но прежде чем это сказать, нужно хорошо подумать, как сделать то, что ты сказал.Что ж, я уже подумал и реализовал придуманный алгоритм с помощью C++ и графической библиотеки OpenGL (+ надстройка GLUT).
Графическая библиотека используется для рисования набора точек в двухмерном пространстве.
Кода оказалось не так уж и мало, но и не так уж и много.
Почти весь код распространяется в заголовочных файлах C++.
Проект выложен в открытый доступ для всех, кто хоть немного заинтересован.
Исходники расположены по адресу Битбакет .
В проекте используется система контроля версий GIT, поэтому у желающих скачать исходный код проекта не должно возникнуть с этим никаких затруднений.
Для перехода в режим программирования фигур необходимо щелкнуть правой кнопкой мыши в главном окне.
Затем нарисуйте рамку (используя точки, соединенные по порядку отрезками) и нажмите среднюю кнопку мыши.
"Сделанный!" появится на экране.
После этого перезапустите приложение.
Подводные скалы
Они есть практически везде.и этот алгоритм не исключение.
Скажу откровенно, алгоритм допускает периодические осечки в правильном распознавании.
Взять, к примеру, символы «S» и «5», где осечки практически неизбежны.
Хотя, если все контрольные точки будут четко обозначены, то, скорее всего, осечек удастся избежать.
Осечки могут возникать и при анализе фигур, имеющих сложную округлость.
Если на разнородных символах возникают осечки (например, у меня были осечки с «6» и «8»: 6 — 100%, 8 — 83%), то можно запрограммировать кадр каждой из цифр заново (количество повторы не ограничены).
Таким образом, вы сможете избежать ошибок распознавания.
И последнее, на что следует обратить внимание, это угол, образованный последней, первой и второй точками + надо запомнить соотношение его сторон.
Для этого можно «выровнять» этот угол до 90 градусов, как показано на демонстрационном видео ниже.
В статье я упомянул только цифры, как вы могли заметить.
Но на самом деле распознавание применимо к абсолютно любым фигурам в двухмерном пространстве.
Еще я сделал небольшое приложение к статье - видео , демонстрирующий работу алгоритма.
Если есть вопросы, задавайте - с удовольствием на них отвечу.
Теги: #Алгоритмы #математика #c++ #программирование #программирование #C++ #Алгоритмы
-
Что Такое Сертификация Mcse?
19 Oct, 24 -
«Я Не Могу Позволить Себе Купить Еду»
19 Oct, 24 -
Пасхальное Яйцо В Блокноте И Калькуляторе
19 Oct, 24 -
Берегите Свои Глаза
19 Oct, 24


