Эксперты по вероятности обнаружили фундаментальные недостатки в проведении множества социологических опросов и психологических тестов, которые проводились за последние 50 лет. Дело в том, что гуманитарии совершенно невежественны в математике.
В частности, они не знакомы Парадокс Монти Холла .
Это неудивительно, ведь данное явление из теории вероятностей противоречит здравому смыслу.
А люди гуманитарного профиля (социологи, психологи и т. д.) проводят свои опросы и подсчитывают результаты, основываясь на здравом смысле и элементарной логике, которая здесь не работает. Вот простой пример когнитивного диссонанса.
В игре «Ой, Счастливчик!» вам даны три возможных правильных ответа.
Вы выбрали один, но добрый ведущий решает вам помочь и закрывает один из трёх ответов, что заведомо неправильно.
Что делать в такой ситуации? Здравый смысл подсказывает, что нет причин отменять свой выбор.
Но теория вероятностей ясно указывает на то, что при изменении варианта ответа ваши шансы на победу парный разряд .
Это примерное описание знаменитого парадокса Монти Холла (подробное описание под аннотацией).
Если учитывать это при проведении социальных опросов и психологических исследований, то результаты многих из них можно интерпретировать по-разному и результаты могут немного измениться.
«Парадокс Монти Холла — одна из известных проблем теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу.
Задача сформулирована как описание гипотетической игры по мотивам американского телешоу «Давай заключим сделку» и названа в честь ведущего этой программы.
Наиболее распространенная формулировка этой проблемы, опубликованная в 1990 году в журнале Parade Magazine, выглядит следующим образом: Представьте, что вы участник игры, в которой вам нужно выбрать одну из трех дверей.
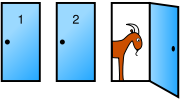
За одной из дверей — машина, за двумя другими — козы.
Вы выбираете одну из дверей, например, номер 1, после чего ведущий, знающий, где находится машина и где находятся козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза.
Затем он спрашивает вас, хотите ли вы изменить свой выбор и выбрать дверь номер 2. Увеличатся ли ваши шансы выиграть машину, если вы примете предложение хозяина и измените свой выбор? Хотя эта постановка задачи является наиболее известной, она несколько проблематична, поскольку оставляет неопределенными некоторые важные условия задачи.
Ниже приведена более полная формулировка.
При решении этой задачи обычно рассуждают примерно так: после того, как ведущий открыл дверь, за которой находится козел, машина может находиться только за одной из двух оставшихся дверей.
Поскольку игрок не может получить никакой дополнительной информации о том, за какой дверью находится машина, вероятность найти машину за каждой дверью одинакова, и изменение первоначального выбора двери игроком не дает игроку никакого преимущества.
Однако такая линия рассуждений неверна.
Если ведущий всегда знает, какая дверь за какой находится, всегда открывает ту из оставшихся дверей, за которой находится коза, и всегда предлагает игроку изменить свой выбор, то вероятность того, что машина находится за выбранной игроком дверью равна 1/3, и, соответственно, вероятность того, что машина окажется за оставшейся дверью, равна 2/3. Таким образом, изменение первоначального выбора увеличивает шансы игрока на выигрыш автомобиля в 2 раза.
Этот вывод противоречит интуитивному восприятию ситуации большинством людей, поэтому описанную проблему называют парадоксом Монти Холла».
Теги: #теория вероятностей #психологические тесты #социологические исследования #Занимательные задачи
-
Ферма, Пьер
19 Oct, 24 -
Обманчивая Видимость Экономики Ссылок
19 Oct, 24 -
Виджет Яндекс.часов К Новому Году
19 Oct, 24 -
7 Типов Собеседований
19 Oct, 24 -
Подкаст Unclesoky - Эпизод №24
19 Oct, 24 -
Истории Разработчиков: Trekkit Traveler
19 Oct, 24


