Постоянная Очередь

Вдохновлен недавним постом «Постоянное декартово дерево по неявному ключу» , решил написать про реализацию постоянной очереди.

Ошиблись те, кто сейчас думал, что раз обычная очередь — это тривиальная структура, то ее персистентная версия должна быть очень простой; результирующая реализация по крайней мере не проще, чем для приведенного выше дерева.

Постановка задачи

Кроме того, нам, конечно, хотелось бы иметь то же асимптотическое время выполнения и дополнительную память, что и для непостоянного варианта, а именно O(n), где n — общее количество операций, выполняемых в нашей очереди.

Кстати, если ослабить требования к O(n log n), то очередь тривиально эмулируется с помощью постоянного декартова дерева с использованием неявного ключа.

Примем следующий простой интерфейс для работы с нашей структурой данных: версии очереди, возникающие в результате запросов, будем нумеровать неотрицательными целыми числами; изначально существует только пустая очередь с номером 0. Пусть у нас есть N версий очередей (включая исходную пустую), тогда они пронумерованы числами от 0 до N-1 и мы можем выполнить следующие четыре запроса:

1. пустой(query_id) — проверяет, пуста ли очередь с заданным номером;
2. front(query_id) — возвращает первый элемент очереди, сама очередь никак не меняется и новые очереди не создаются.

   Операция допустима, если очередь не пуста;

3. push(query_id, new_element) — создает новую очередь с номером N, полученную добавлением нового элемента в конец исходного.

   Старая версия по-прежнему доступна под номером query_id;

4. pop(query_id) — создает новую очередь с номером N, полученную путем извлечения первого элемента из исходной.

   Исходная очередь по-прежнему доступна под старым номером.

   Если исходная очередь была пуста, новая также будет пустой.

Моделирование очереди с использованием стеков

Для каждой проблемы есть решение — простое, быстрое и неправильное.

— Первый закон онлайн-судей

Кроме того, мы знаем, что очередь можно смоделировать с помощью двух стеков.

Возникает очевидная идея: давайте сделаем эти два стека постоянными и проблема решена! К сожалению, этот простой подход не сработает. Дело в том, что при таком моделировании не каждая операция имеет асимптотику O(1): если во время pop стек, из которого мы берем элементы, оказывается пустым, то мы перекладываем в него все элементы из другого стека.

В случае регулярной очереди каждый элемент сдвигается только один раз, поэтому общая асимптотика остается O(n), но в персистентном случае каждый элемент может принадлежать многим очередям и, соответственно, смещаться несколько раз.

Пусть, например, q — номер очереди, стек которой пуст, тогда после push(q, 1) и push(q, 2) в результирующих очередях этот стек останется пустым и при извлечении из них каждый элемент очередь q будет перемещена дважды.

Невозможно организовать какое-либо совместное использование сдвинутых элементов из-за того, что нижние элементы стеков, полученные сдвигом, будут разными (1 и 2 соответственно), а постоянный стек устроен таким образом, что каждый элемент хранит указатель на элемент, лежащий под ним.

поэтому в любом случае мы будем вынуждены иметь 2 копии предпоследнего элемента, которые будут указывать на соответствующий последний, а значит 2 копии предпоследнего элемента, чтобы указывать на нужный предпоследний, и так далее по порядку.

цепь.

Тем не менее есть алгоритм , основанный на этой идее (имитация очереди с использованием двух стеков), гарантирующий, что стек, из которого мы извлекаем данные, никогда не будет пустым, и использование 6 стеков для обеспечения этого.

Мой алгоритм явно не использует эту идею, хотя общие моменты, конечно, можно найти.

Описание алгоритма

предыдущий элемент является вершиной дерева).

Когда я буду ссылаться на элемент очереди в будущем, я часто буду иметь в виду вершину, соответствующую этому элементу.

Непустая очередь в этом случае может быть представлена парой указателей на первый и последний элемент очереди, причем вершина, соответствующая первому элементу, обязательно будет предком вершины, соответствующей последнему (ну, или совпадают с ним в случае очереди из одного элемента).

Пример такой структуры и как в ней отображается очередь: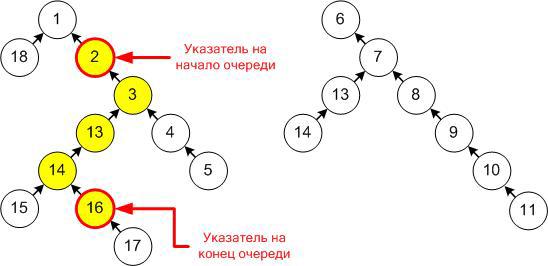



Обратите внимание, что операция push просто создает новую вершину, устанавливая последний элемент исходной очереди в качестве ее родителя (или он становится новым корнем, если добавить его к пустому), а операция pop вообще не затрагивает наш лес, она просто перемещает указатель на первый элемент. Таким образом, после создания вершина остается неизменной до конца операции и можно не беспокоиться, что новые операции могут как-то испортить существующие очереди.

Наша единственная проблема с этим подходом - реализация операции pop (остальные три тривиальны), неясно, как определить, на какую вершину переместить указатель на первый элемент, потому что для вершины мы храним только указатель на родительскому, но не дочерним (которых у одной вершины может быть несколько штук, и даже если мы сохраним их все, совершенно непонятно, какая из них соответствует следующему элементу в нашей очереди).

Поэтому для каждой очереди, имеющей более двух элементов, мы дополнительно будем хранить указатель на элемент некоторого односвязного списка, такого, что элемент списка по нашему указателю содержит указатель на второй элемент нашей очереди, и элементы под ним в списке являются указателями на третий.

четвертый и так далее соответственно.

Имея такой указатель на исходную очередь, нам теперь при выполнении попса не составит труда определить новый заголовок очереди, а указатель на такой элемент списка для результирующей очереди является просто указателем на следующий элемент в этом списке.

Однако по причинам, аналогичным тем, почему эмуляция очереди с двумя стеками не работает, мы не сможем гарантировать, что для каждой очереди ниже списка имеются абсолютно все ее промежуточные вершины, поэтому пусть она содержит ровно столько, сколько тогда первый из них, а мы, когда этот список начнет становиться слишком маленьким, будем строить новый список, перемещаясь шаг за шагом (то есть увеличивая строящийся список на 1 элемент при каждой операции push или pop) от конца очередь в начало, следуя указателям на родителей вершин нашего дерева и стараясь добиться того, чтобы к моменту окончания старого списка у нас уже был наготове новый.

Говоря более формально, для каждой очереди помимо указателей на начало и конец и указателя на элемент готового списка мы будем хранить еще указатель на элемент строящегося списка (если мы не строим что угодно, оно будет равно 0) и вычислим его значение для новой очереди (полученной после применения push или pop к исходной) по следующему простому алгоритму:

• если в исходной очереди этот указатель был равен 0, проверим, не пора ли нам приступить к построению нового списка (критерий такой проверки будет описан ниже):
  • если пришло время, то мы создаем элемент списка с нулевым указателем на следующий элемент в списке (при этом этот созданный элемент будет концом построенного списка), а указатель на вершину помещаем на предпоследний элемент нашего списка.

    очередь (родительский элемент последнего элемента),

  • если еще не время, то указатель остается равным нулю.

• В случае ненулевого начального указателя мы построим наш список по одному элементу: создадим новый элемент, указывающий на исходный как следующий в списке и на родителя вершины, соответствующей этому исходному указателю.

  элемент.

Изображение того, как все это работает и что происходит во время нажатия или нажатия, можно увидеть на схеме (как я ни старался, понятнее сделать не удалось):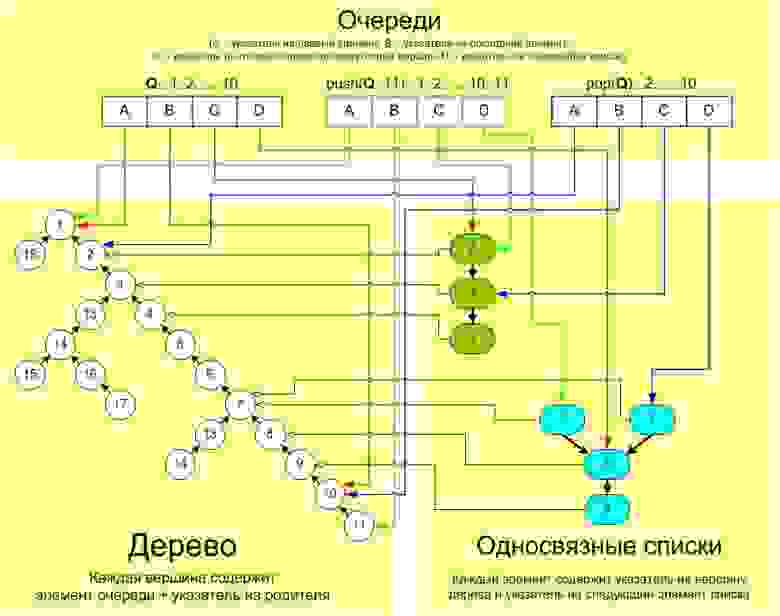



Соответственно, если при заполнении списка мы доходим до первого промежуточного элемента, то построение этой очереди завершается (при этом некоторые другие очереди могут продолжать дополнять этот список, но так как старые элементы никогда не меняются, то это будет нам никоим образом не навредить).

В этом случае вместо указателя на элемент старого списка мы записываем указатель на элемент нового, а указатель на построенный список присваиваем нулю.

Из описания алгоритма видно, что при выполнении каждого запроса мы создаем не более одной новой вершины дерева и не более одного нового элемента списка и тратим на его выполнение O(1), т.е.

асимптотика — это то, к чему мы стремились, и остается только обсудить правильный критерий.

Проверка критерия начала строительства

Заметим, что если промежуточных вершин нет, то мы имеем неравенство 0 ≥ 0 и ничего не делаем, то есть нет необходимости выделять это как частный случай.

Докажем, что при таком подходе мы никогда не окажемся в ситуации, когда старый список закончился, а новый еще не готов.

Для начала докажем следующий инвариант: если построить новый список, то на каждом шаге 2k + l = s, где k — количество элементов в старом списке, l в построенном (после завершения уже завершено на этом этапе), s — общее количество промежуточных элементов.

Докажем это методом математической индукции.

Рассмотрим первый шаг, когда мы только начали проектировать (l = 1).

Обратите внимание, что для новой очереди 2k – s < 0 (our criterion), however for the original 2k _старый -с _старый ≥ 0. Давайте посмотрим, как это может произойти: если наша операция push, то k = k _старый , и s = s _старый +1, а если pop, то k = k _старый – 1 и s = s _старый – 1. Как легко видеть, в обоих случаях 2k – s меньше 2k. _старый -с _старый ровно на единицу, а так как обе разности целые числа, значит, вторая из них равна 0, а первая равна -1, следовательно, 2k + 1 = s, и наш l равен всего лишь единице.

Основа индукции доказана.

Докажем переход: пусть на некотором шаге построения 2k _старый + л _старый = с _старый .

Тогда l = l _старый +1 (мы дополнили список на 1 элемент), в случае push: k = k _старый , с = с _старый + 1, в случае поп: k = k _старый – 1, с = с _старый – 1. В обоих случаях равенство выполнено, а значит, утверждение доказано.

Теперь предположим, что мы выполняем операцию pop, и в исходной очереди есть нужный нам пустой список (при отправке мы этот список никак не используем).

Тогда это может быть одно из двух:

• или для исходной очереди мы не начали строить новый список, то в этой очереди 2k ≥ s, k = 0 => s = 0, что означает, что это очередь размером 0, 1 или 2, и знания ее последнего элемента достаточно, чтобы выполнить pop,
• или началось, то l ≠ 0, в силу инварианта 2k + l = s, k = 0 => l = s ≠ 0 => построенный список был непустым и содержал все промежуточные элементы, а значит, нам пришлось сделать замену на этом шаге и получите непустой список.

длина полученного списка составляет не менее 1/2 от общего числа промежуточных вершин, иными словами, что при момент завершения 2l ≥ s или, что эквивалентно, l ≥ s –l. Но что такое s–l? Это количество промежуточных вершин, которых нет в нашем списке.

Легко понять, что оно равно количеству операций push, произошедших в процессе проектирования.

Однако при каждой такой операции количество элементов в нашем списке тоже увеличивалось на 1 (возможна ситуация, когда на предыдущем шаге элемент построенного списка соответствует третьему элементу очереди и мы делаем pop, тогда для новой очереди элемент списка начинает соответствовать первому промежуточному элементу сразу без завершения, но это возможно только на последнем этапе проектирования и только во время операции pop).

Следовательно, l ≥ количества таких толчков (нетрудно понять, что оно даже строго больше), что и требовалось доказать.

Для наглядности продемонстрируем, что происходит в двух крайних случаях: когда мы все время толкаем и когда мы все время толкаем: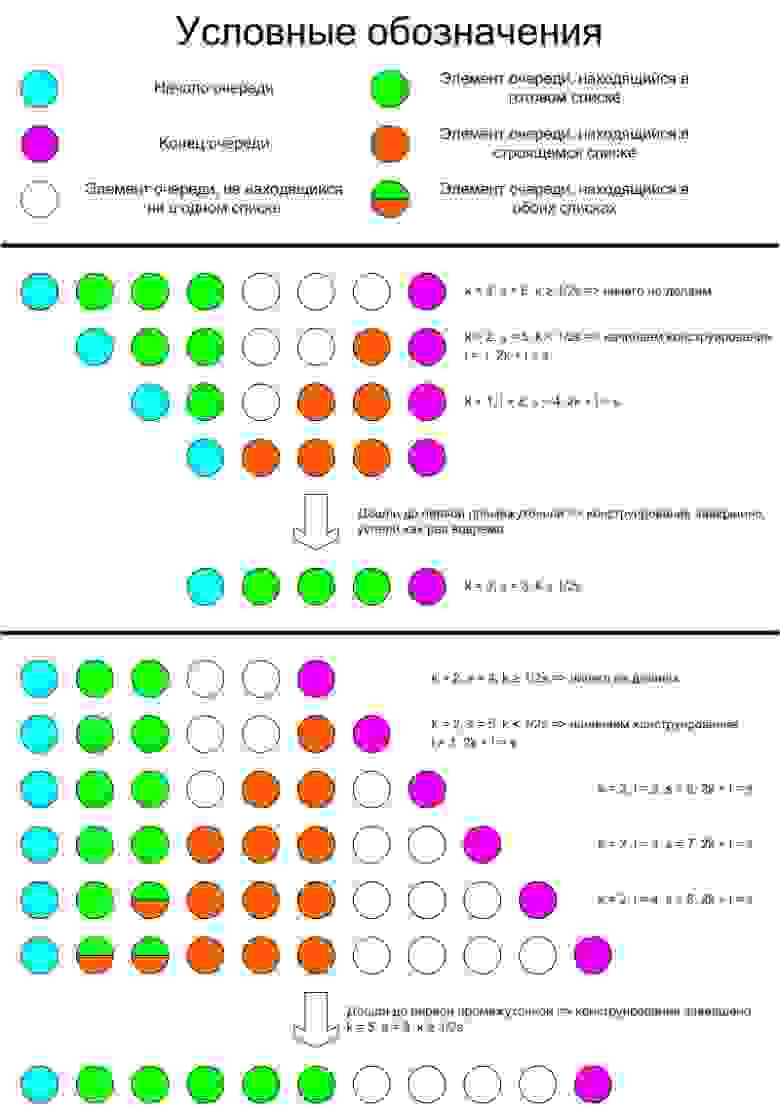

Реализация на C++

Этот код стоит взять за прототип; Я постарался написать максимально просто и кратко, пожертвовав ради этого всем остальным.

persist_queue.h

   

 #ifndef PERSISTENT_QUEUE_H
 #define PERSISTENT_QUEUE_H
 
 #include <cstdlib>
 #include <vector>
 
 using Element_type = int;
 
 class Persistent_queue {
 

   

• Партнеры: Преимущества И Недостатки Приобретения Собственного Программного Обеспечения Для Отслеживания Партнеров

  19 Oct, 24

• Психология Платных Онлайн-Опросов

  19 Oct, 24

• Прямая Трансляция Из Сан-Франциско: Конференция Apple Wwdc 2016

  19 Oct, 24

• Создание Интерфейса Для Игры

  19 Oct, 24

• Как Краудсорсинговая Платформа Яндекса Помогает Обучать Алису И Экономить Деньги

  19 Oct, 24

• Нейтринные Осцилляции Для Чайников

  19 Oct, 24

• Swiftfox — Альтернативная Сборка Firefox

  19 Oct, 24

• Огненная Лисица В России.

  19 Oct, 24

• Что Происходит С Mootools

  19 Oct, 24

• Обновление Плагина Mctube

  19 Oct, 24