Несколько дней назад я провел онлайн-конкурс по игре .
В онлайн-конкурсе приняли участие 1199 человек, а решений было более 5000, среди которых 61 решение представляло собой попытки обхода системы путем поиска уязвимостей.
Это очень круто, спасибо всем, кто принял участие.
?Эта игра представляет собой тип « Игры полковника Блотто В нем принимают участие два игрока.
У каждого одинаковое количество ресурсов, которые нужно разместить на поле NxM. Победителем становится тот, кто займет больше клеток (т. е.
количество ваших ресурсов на нем больше, чем у вашего оппонента).
Вот так выглядит условие нашей задачи.
Состояние 1. Играют два человека.
2. Игровое поле представляет собой доску 3 на 3. 3. У каждого игрока есть армия из 100 космических десантников.
4. Перед боем ночью каждая сторона тайно в случайном порядке размещает свои войска на 9 клетках.
На каждой ячейке можно разместить любое целое число космодесантников от 0 до 100. 5. Утром начинается битва за следующую планету.
На каждой из 9 клеток побеждает игрок, у которого на этой клетке больше всего Астартес.
За победу на каждом из 9 квадратов дается 1 очко.
Если в определенной ячейке одинаковый номер, то бой на этой ячейке заканчивается вничью, и оба игрока получают по 0,5 очка.
6. В битве побеждает тот, кто выиграет больше полей.
Если оба игрока выигрывают по 4,5 клетки, битва заканчивается вничью.
Когда я начинал этот эксперимент, я еще не знал, что у этой игры нет идеального решения, но благодаря комментариям я смог лучше разобраться в этой теме.
Начнем с победителей этой игры 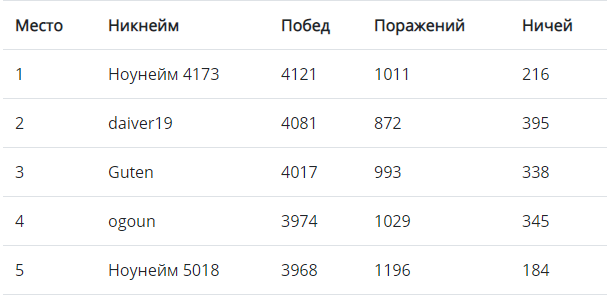
Решение Noname 4173 
Лучшее решение набрало 4121 победу – очень хороший результат. Но что было бы, если бы в игре были задействованы только решения из ТОП-100? 
Удивительно, но оно не попало даже в топ-5 (на 8-м месте), а 1-е место здесь заняло решение с 68-го места.
Арем решение 
Это просто показывает, что лучшего решения не существует. Остальные результаты можно посмотреть на сайте game.pavlukhinlab.com
Но что еще интересного можно узнать?
Игроки размещали самые большие числа в центре, при этом все игроки в среднем заполняли первый ряд более крупными числами, в то время как лучшие игроки уделяли больше внимания нижнему ряду.


средние значения по всем играм (слева) и ТОП-100 (справа)
Ну и вот еще несколько примеров лучших стратегий: Примеры стратегий Огуна (6 решений в ТОП-100) 

Примеры стратегий Гутена (8 решений в ТОП-100) 

Лучшие стратегии выбрали 5 основных ячеек, остальные ячейки были заполнены небольшими значениями.
Что логично, ведь для победы достаточно занять 5 клеток.
Ну а теперь немного графиков.
Вероятностные распределения чисел: 
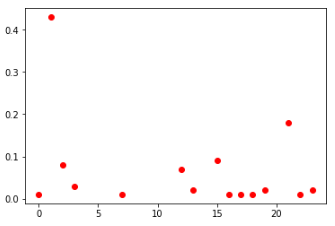
вторые ячейки среди всех игроков (слева) и ТОП-100 (справа) 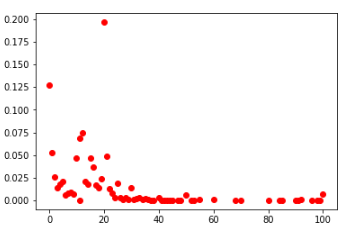
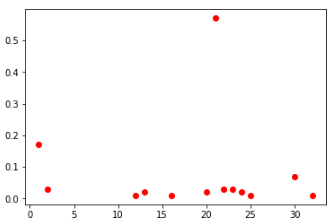
центральные ячейки среди всех и ТОП-100 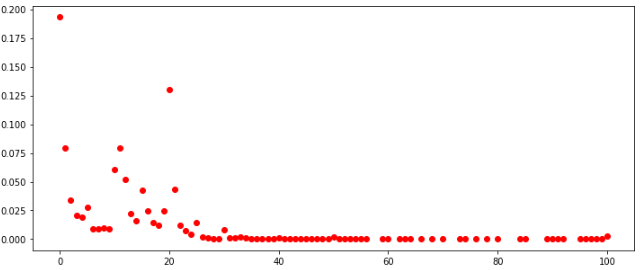
распределение номеров для всех игр 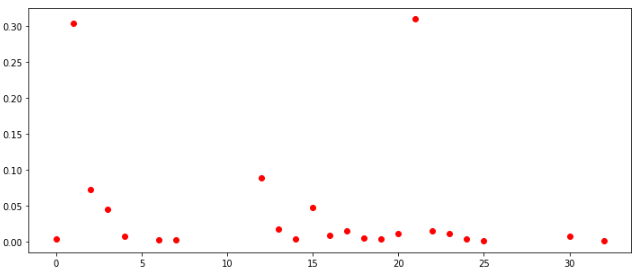
распределение номеров по ТОП-100
Если посмотреть на распределения по всем ячейкам среди всех игроков, то они в целом выглядят одинаково.
Также можно сделать вывод, что в этих условиях нет смысла заполнять ячейки значениями больше 30. На этом исследование завершается – это все, что мне удалось извлечь из этих данных.
Возможно, кто-то из вас подскажет что-то еще, что можно проверить — жду вас в комментариях.
Поиск обезличенных игр по связь .
Пы.
Сы.
В предыдущем посте я рассказывал о нейроне, который учился играть в эту игру.
К сожалению, из этого пока ничего не вышло.
Два нейрона решили, что лучшая стратегия — выбросить на выходе нули и порадоваться ничьей.
Но, возможно, я изучу эту тему и сделаю отдельный пост, посвященный ошибкам, которые я допустил при создании нейрона, а, возможно, и успехам.
Теги: #математика #Логические игры #теория игр #Игры «Полковник Блотто»

-
Хабрахабр Присвоил Каждому «Собаку»
19 Oct, 24 -
Видеообзор Вектор Тд 2
19 Oct, 24 -
Opera Turbo Больше Зла Или Добра?
19 Oct, 24 -
Что Делает Хорошего Программиста Хорошим?
19 Oct, 24


