Комбинаторика в старших классах обычно ограничивается словесными задачками, в которых нужно применить одну из трех известных формул – для числа сочетаний, перестановок или расстановок.
В институтских курсах по дискретной математике говорят и о более сложных комбинаторных объектах - скобочных последовательностях, деревьях, графах.
При этом, как правило, задача состоит в том, чтобы вычислить количество объектов заданного типа для некоторого параметра n, например, количество деревьев на n вершинах.
Выяснив количество объектов при фиксированном n, можно задать более сложный вопрос: как можно представить все эти объекты за разумное время? Алгоритмы, решающие задачи такого рода, называются алгоритмами комбинаторной генерации.
Например, таким алгоритмам посвящена первая глава четвертого тома «Искусства программирования» Дональда Кнута.
Кнут очень подробно обсуждает алгоритмы генерации всех кортежей, числовых разделов, деревьев и других структур.
Нетрудно придумать некий алгоритм, работающий умеренно быстро для каждой из этих задач, но при дальнейшей оптимизации могут возникнуть серьезные проблемы.
В процессе написания магистерской диссертации, защищенной в Академический университет Мне нужно было изучить и применить один из алгоритмов комбинаторной генерации, подходящий для особого класса задач.
Это генерация структур, на которых дополнительно вводится некоторое отношение эквивалентности.
Чтобы было понятно, о чем идет речь, приведу простой пример.
Попробуем сгенерировать все триангуляции шестиугольника.
Вы получите что-то вроде этого: 
Написать алгоритм, который будет возвращать все такие триангуляции, довольно легко.
Например, подойдет следующая процедура: фиксируем какое-то ребро (пусть это будет ребро 1-6), после чего перебираем вершины, не являющиеся его концами.
Мы строим треугольник по текущей вершине и фиксированному ребру, а затем рекурсивно триангулируем оставшиеся две области.
Если вы присмотритесь к триангуляциям, возникающим в результате работы этого алгоритма, то заметите, что многие из них практически идентичны и отличаются только тем, как расставлены метки вершин (цифры).
Поэтому было бы полезно придумать алгоритм, который будет генерировать так называемые неразмеченные триангуляции — те, что показаны на следующем рисунке: 
Более формально, пусть некоторые действуют на наш набор объектов.
отношение эквивалентности , разделив все множество на классы изоморфный объекты друг другу.
Требуется сгенерировать по одному представителю от каждого класса.
Вы наверняка заметили, что две правые триангуляции на второй картинке тоже очень похожи друг на друга и оставить из них можно только одну.
На самом деле все зависит от того, какое отношение эквивалентности мы выберем.
Если считать изоморфными только те триангуляции, которые после поворота могут накладываться друг на друга, то их будет четыре, а если еще допустить возможность переворота шестиугольника, то три.
Казалось бы, сгенерировать по одному представителю от каждого класса несложно: генерируем все объекты, затем попарно проверяем их на изоморфизм и выбрасываем дубликаты.
К сожалению, для некоторых типов объектов это займет ужасно много времени даже при небольшом n. Они не могут решить задачу проверки изоморфизма, например, двух графов за полиномиальное время, а значит, подпрограмму, решающую эту задачу, желательно вызывать как можно реже.
Еще одним недостатком предлагаемого наивного подхода является то, что все объекты придется хранить в памяти одновременно.
При этом, если теоретически можно дождаться, пока медленная программа выдаст правильный ответ, то получить вместо ответа переполнение памяти совершенно недопустимо.
Итак, чтобы сгенерировать попарно неизоморфные объекты, нужно использовать еще какой-то хитрый метод. Этот метод был неоднократно переоткрыт для многих конкретных комбинаторных объектов (графов, деревьев, разбиений) и в общем виде описан в статье Исчерпывающая генерация без изоморфов .
Об этом методе я расскажу на примере задачи, несколько более общей по сравнению с задачей триангуляции: мы сгенерируем все «разрезы», то есть способы разбиения многоугольника не обязательно на треугольники, а на многоугольники с количество сторон из списка, который предоставляется в качестве входной программы.
Для описания этого метода необходимо несколько формальных определений.
Пусть X — некоторый набор «структур».
Элементы множества X будем называть отмеченные объекты .
В нашей задаче помеченные объекты представляют собой разрезы, вершины которых пронумерованы против часовой стрелки.
Структура данных для помеченных разрезов проста — это списки смежности:
Пусть G будет некоторым группа перестановки, действующие на множестве X. Это означает, что каждый помеченный объект x из X и каждый элемент g группы G связан с другим помеченным объектом y = g*x, и выполняются следующие свойства:public class Dissection { private int[][] adjacent; .}
- Умножение любых элементов группы h и g соответствует последовательному применению действий к объекту x: h*(g*x)=(hg)*x.
- Групповая единица e переводит каждый помеченный объект x в себя: e*x=x.
маркировка вершин.
Эти классы эквивалентности изображены на втором рисунке.
Мы назовем эти классы непомеченные объекты .
Каждому элементу X мы сопоставляем натуральное число, которое будем называть порядком.
Порядок всех эквивалентных объектов должен быть одинаковым.
Это свойство позволяет дополнительно определить порядок классов эквивалентности (немаркированных объектов): он будет равен порядку любого представителя соответствующего класса.
Для нашего примера на рисунке порядок — это количество вершин в многоугольнике.
Для всех непомеченных объектов на рисунке оно равно шести.
Это были довольно общие определения.
Теперь перейдем к определениям, специфичным для будущего алгоритма.
Каждому помеченному объекту x мы связываем два набора: набор нижние объекты L(x) и множество топ объектов У(х).
Порядок элементов в этих наборах по определению равен порядку x. Прежде чем дать формальные требования к нижним и верхним объектам, я попытаюсь дать интуитивное описание.
Каждый нижестоящий объект должен содержать информацию о том, как однозначно перейти от текущего объекта к объекту более низкого порядка.
Например, нижний объект разреза — это разрез, в котором дополнительно выделен один из «крайних» полигонов (например, окрашенный в красный цвет), который можно отрезать от этого разреза.
Верхний объект, наоборот, — это помеченный объект плюс информация, позволяющая его однозначно «увеличивать», повышая порядок.
Например, верхний разрез — это разрез, при котором одна из сторон многоугольника дополнительно выделена (например, окрашена в красный цвет) и на ней написано число.
Глядя на этот разрез, мы можем выяснить, к какой стороне приклеить новый многоугольник, чтобы увеличить порядок.
Количество сторон склеенного многоугольника будет определяться числом, написанным на ребре.
Эту идею можно проиллюстрировать следующим рисунком, на котором изображены два объекта — нижний и верхний, соответствующие одному и тому же разрезу.

В программе нижний и верхний срез представлены следующим образом: public class LowerDissection {
private Dissection dissection;
private int after;
.
}
public class UpperDissection {
private Dissection dissection;
private int after, size;
.
}
Для нижнего разреза мы сохраняем только номер вершины, с которой начинается многоугольник, который мы собираемся удалить.
Для верхнего среза сохраняется номер вершины, после которой нужно будет склеить новый многоугольник, а также количество его сторон.
Вы можете заметить, что некоторые из нижнего и верхнего объектов находятся в отношениях «соответствия»: нижний объект соответствует верхнему, что получается после того, как мы уменьшили порядок так, как закодировано в нижнем объекте.
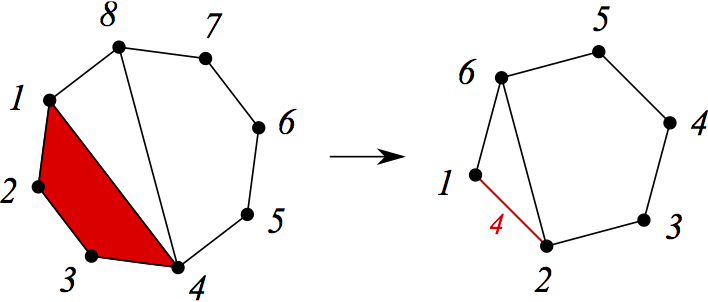
Здесь нижний объект сопоставляется с верхним, что является результатом удаления выбранного четырехугольника.
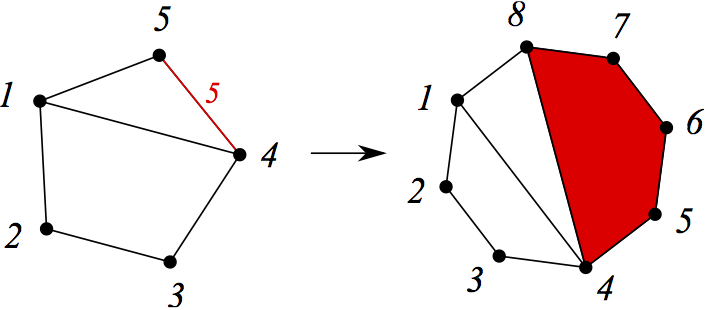
На следующей картинке все наоборот: к верхнему объекту, точнее, к его выбранному краю приклеен пятиугольник с написанной на нем пятеркой.
В результате создается объект нижнего уровня, в котором хранится информация о том, как откатить завершенную операцию.
Теперь формально, что нужно потребовать от упомянутых структур:
- Группа G действует на три типа объектов: отмеченные, верхние и нижние.
Каждое из этих трех множеств замкнуто под действием группы (это означает, что, например, если элемент группы воздействует на нижний объект, невозможно получить верхний - достаточно формальное требование).
- Для каждого помеченного объекта x и элемента группы g: L(g*x)=g*L(x); U(g*x)=g*U(x) (обозначение g*L(x) означает, что мы применяем g к каждому элементу множества L(x), аналогично g*U(x)).
- Для каждого нижнего объекта y соответствующее множество верхних объектов не пусто.
- Если два нижних объекта y и x эквивалентны (то есть y=g*x), то любые два соответствующих верхних объекта также эквивалентны.
- Если два верхних объекта y и x эквивалентны, то любые два соответствующих нижних объекта также эквивалентны.
- Порядок нижнего объекта больше порядка любого соответствующего верхнего объекта.
Отвечать Конечно, это не единственный способ, но в качестве нижних объектов вполне естественно взять графы без треугольников, у которых одна из вершин окрашена в красный цвет (это будет означать, что мы собираемся ее удалить), а графы без треугольников, в котором несколько вершин окрашены в красный цвет (это будет означать, что мы собираемся добавить вершину и соединить ее со всеми красными вершинами).
В этом случае необходимо потребовать, чтобы красные вершины не были соединены попарно.
В этом случае после добавления новой вершины треугольники не образуются.
Давай продолжим.
Предположим, что от какого-то немаркированного предмета ничего нельзя «откусить».
Таким образом, не существует низших объектов, соответствующих ему (точнее, соответствующих его помеченных объектов).
Такой объект называется нередуцируемый .
В нашем случае разрезы, состоящие из одного многоугольника, являются неприводимыми.
Все остальные данный .
Наш алгоритм будет генерировать все неизоморфные разрезы последовательно, начиная с неприводимых, постепенно увеличивая их порядок.
Для этого мы приклеим к текущему разрезу все возможные полигоны со всех возможных сторон.
Проблема, однако, в том, что одного и того же рассечения можно достичь более чем одним способом.
Например, рассечения восьмиугольника, который на двух предыдущих картинках соответствовал нижнему предмету, можно добиться, приклеив к треугольнику четырехугольник, а затем пятиугольник, или, наоборот, приклеив треугольник и четырехугольник к пятиугольник.
Таким образом, появляется возможность генерировать одно и то же рассечение несколько раз, даже не замечая этого.
Это именно то, чего вы хотите избежать.
Чтобы обойти эту проблему, при создании нового разреза мы проверим, соответствует ли последнее добавление полигона единственному каноническому способу построения этого разреза.
Для этого нам нужна функция P, которая связывает каждый помеченный объект с набором объектов более низкого уровня, для которых он является «дочерним».
Функция P должна удовлетворять следующим требованиям:
- Если L(x) пусто, то P(x) также пусто.
- Если L(x) не пусто, то P(x) состоит из таких и только таких нижних объектов, соответствующих объекту x, что любые два из них преобразуются друг в друга под действием некоторого элемента g, для которого g*x=x.
- Для любого непомеченного объекта x и элемента группы g: g*P(x)=P(g*x).
Тогда P(x) должен состоять ровно из двух нижних объектов, возникающих друг из друга с помощью таких вращений.
Попробуем удовлетворить общее требование в нашем примере.
Для этого возьмем некоторый разрез x и прокрутим на нем метки всеми n способами (n — количество вершин).
Каждый раз, когда «крайний» полигон начинается с вершин 1 и 2 (той, которую можно отрезать), мы будем запоминать эту нумерацию.
После этого из всего выбранного подмножества нумераций вершин выбираем те, которые обеспечивают лексикографически минимальную (подойдет любой другой разумный порядок) запись для списков смежности.
Эти нумерации дают нам некоторые многоугольники на исходном объекте x — те, которые при соответствующих нумерациях начинаются с 1 и 2. P(x) как раз состоит из нижних объектов для x, у которых эти многоугольники окрашены в красный цвет. Здесь без картинки не обойтись: 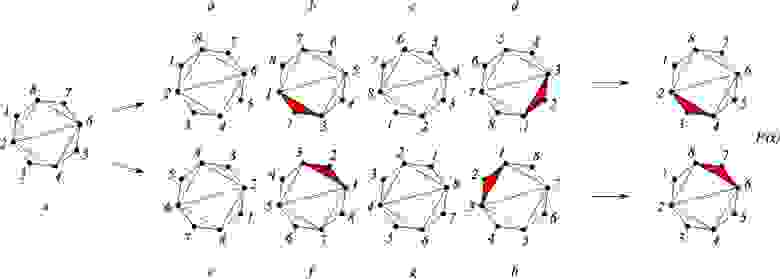
Итак, мы выбрали раздел x, показанный слева, и переставили метки восемью различными способами.
Методы a, c, e и g нам сразу не подходят: не существует многоугольника, построенного на вершинах 1,2,.
,i, который можно было бы отрезать.
Видно, что методы b и f по существу одинаковы, как и методы d и h. Из этих четырех методов мы выбираем те, которые в некотором смысле являются «минимальными».
Как мы уже отмечали, определять минимум можно как угодно, но однозначно.
Например, подойдет лексикографически минимальная нотация для списков смежности.
В этом случае побеждают методы b и f. Этот метод дает нам треугольники 2,3,4 и 6,7,8 на исходном отмеченном объекте x. В результате мы получаем два нижних объекта, показанных на картинке справа.
Функция P является наиболее важной для быстрой генерации.
Удовлетворить этим требованиям и поддерживать высокую скорость на самом деле довольно сложно.
Как видите, функция P в некотором смысле позволяет указать, какой из способов «откусить» крайний многоугольник является каноническим, с точностью до изоморфизма.
Если концепция ясна, предлагаю вам разобраться, как должна работать функция P(x) для уже упомянутых графиков без треугольников.
Отвечать Ответ, конечно, не однозначен.
Один из простых (но не очень эффективных) методов таков: для графа без треугольников x перенумеруем все способы перенумерации вершин, а затем оставим те, которые дают лексикографически минимальное представление списков смежности.
Для каждого из этих методов мы выбираем вершину v, имеющую номер 1, и создаем нижний объект — граф x с вершиной v, окрашенной в красный цвет. Все такие различные низшие объекты образуют результат работы Р(х).
Лучше посмотреть код, добавляющий методы, реализующие все перечисленные функции, к классам, описанным выше в разделе репозитории : Слишком много технических деталей, чтобы обсуждать их подробно.
Теперь все готово для описания самого алгоритма генерации.
Он будет работать для каждого неприводимого рассечения.
Для текущего разбора мы рассматриваем все неизоморфные способы создания верхнего объекта, а затем встраиваем каждый полученный верхний объект в нижний в возрастающем порядке.
Далее, используя функцию P, мы проверяем каждый нижний объект, действительно ли он является родителем соответствующего помеченного объекта.
Если эта проверка пройдена, то мы считаем, что этот помеченный объект является представителем нового класса эквивалентности; мы запускаем для него алгоритм рекурсивно.
Доказать корректность этого алгоритма, конечно, можно, но я чувствую, что уже немного переусердствовал с формализмом, и чтобы понять доказательство, проще обратиться к оригинальная статья .
А еще лучше давайте сначала посмотрим на код, отвечающий за генерацию: public static void generateSubtreeFrom(Dissection root, int maxOrder) {
for (UpperDissection upper : root.createAllUpper()) {
LowerDissection lower = upper.createArbitraryLower();
if (lower != null) {
Dissection probableChild = lower.getUnderlyingDissection();
if (probableChild.getOrder() <= maxOrder && lower.isParentFor(probableChild)) {
root.addChild(probableChild);
generateSubtreeFrom(probableChild, maxOrder);
}
}
}
}
А теперь — результат генерации всех неизоморфных разрезов на 3, 4 и 5-угольников, до порядка, равного восьмому.
Стрелки направлены от родителей к потомству.
Видно, что все разрезы образовали деревья, корни которых являются неприводимыми объектами.
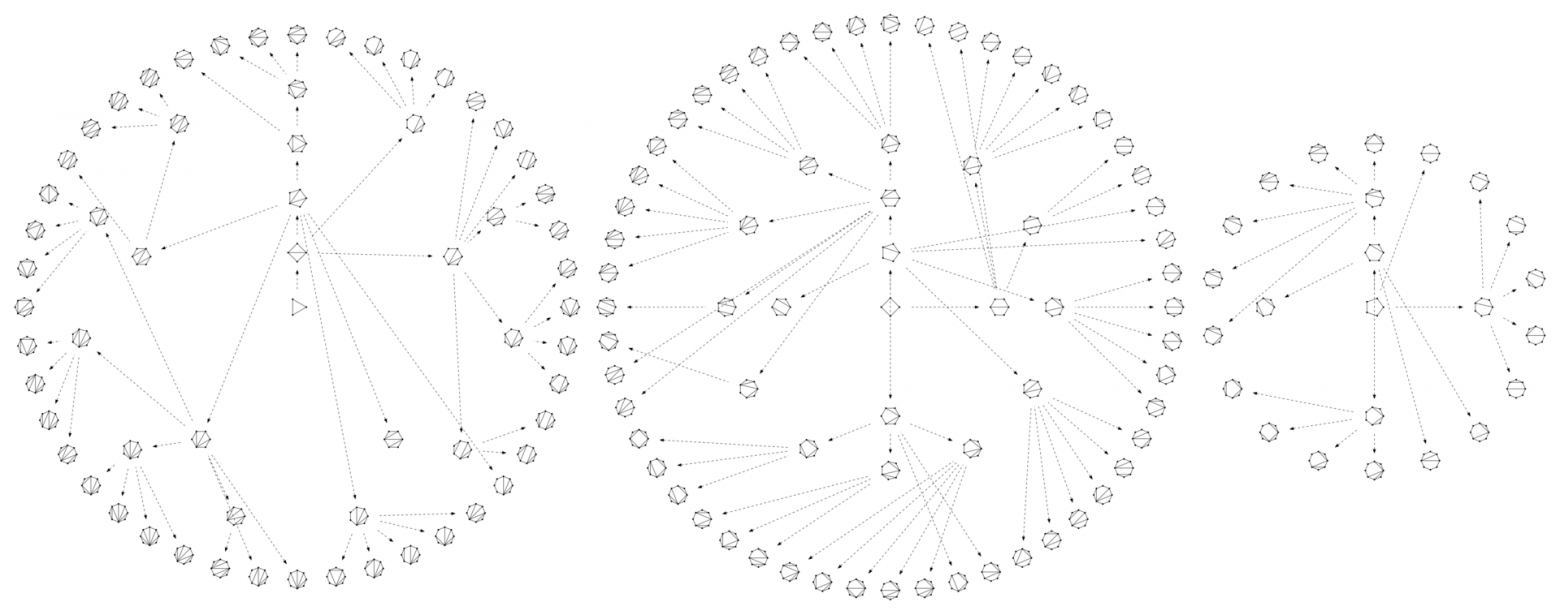
Исходный код программы, создавшей этот рисунок, доступен по адресу Google-код .
Результатом ее работы является описание в формате графвиз.
В заключение добавлю, что для рассматриваемой задачи в принципе можно придумать более простой и в то же время более быстрый алгоритм.
Однако описанная процедура применима практически ко всем типам комбинаторных объектов, которые можно построить индуктивно, «выстраивая» структуру.
Более того, для некоторых типов графов, по крайней мере, по мнению автора алгоритма, такой подход дает одни из лучших, если не лучшие, скорости генерации на сегодняшний день.
Теги: #математика #Алгоритмы #комбинаторика

-
Как Преобразовать Dvd В Файлы Mkv?
19 Oct, 24 -
Foss-Проекты В России
19 Oct, 24 -
Я Даю Тебе Идею
19 Oct, 24 -
Вопросы О Продвижении Android-Приложений
19 Oct, 24 -
Сельский Хакатон В Финляндии
19 Oct, 24


