Другими словами, это удобный способ организации двенадцати нот хроматической гаммы.
Впервые был проведен круг четвертых и пятых квинт. описал в книге «Идея музыкальной грамматики» 1679 года русско-украинского композитора Николая Дилецкого.

Страница из книги «Идея грамматики музыканта», на которой изображен квинтовый круг.
Начать строить круг можно с любой ноты, например до.
Далее, двигаясь в сторону увеличения высоты звука, откладываем одну пятую (пять шагов или 3,5 тона).
Первая квинта — до-соль, поэтому за тональностью до-мажор следует тональность соль-мажор.
Потом прибавляем еще пятую и получаем Б-Г.
Ре мажор — третья тональность.
Повторив этот процесс 12 раз, мы в конечном итоге вернемся обратно к тональности до мажор.
Квинтовый круг называется квинтовым, потому что его также можно построить с помощью кварт. Если взять ноту «до» и понизить ее на 2,5 тона, то получится также нота «соль».
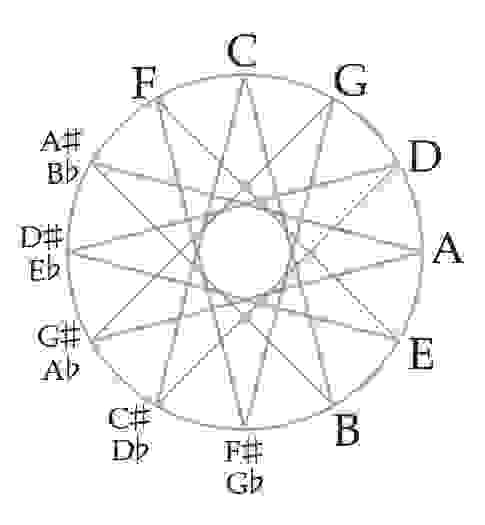
Ноты соединяются линиями, расстояние между которыми равно полутону.
Гейл Грейс (англ.
Гейл Грейс ) примечания , что квинтовый круг позволяет подсчитать количество знаков в тональности той или иной тональности.
Каждый раз, отсчитывая 5 шагов и двигаясь по кругу квинт по часовой стрелке, мы получаем тональность, в которой количество диезов на один больше, чем в предыдущем.
Тональность до мажор не содержит случайностей.
В тональности соль мажор один диез, а в тональности до-диез мажор — семь.
Чтобы посчитать количество плоских знаков в ключе, нужно двигаться в обратном направлении, то есть против часовой стрелки.
Например, начав с до и отсчитывая квинту, вы получите тональность фа мажор, имеющую один бемоль.
Следующей тональностью будет си-бемоль мажор, в которой на тональности стоят два бемольных знака и так далее.
Что касается минора, то минорные гаммы, идентичные мажорным по числу знаков в тональности, представляют собой параллельные (мажорные) тональности.
Определить их довольно просто; вам просто нужно построить минорную терцию (1,5 тона) вниз от каждой тоники.
Например, параллельной минорной тональностью до мажор будет ля минор.

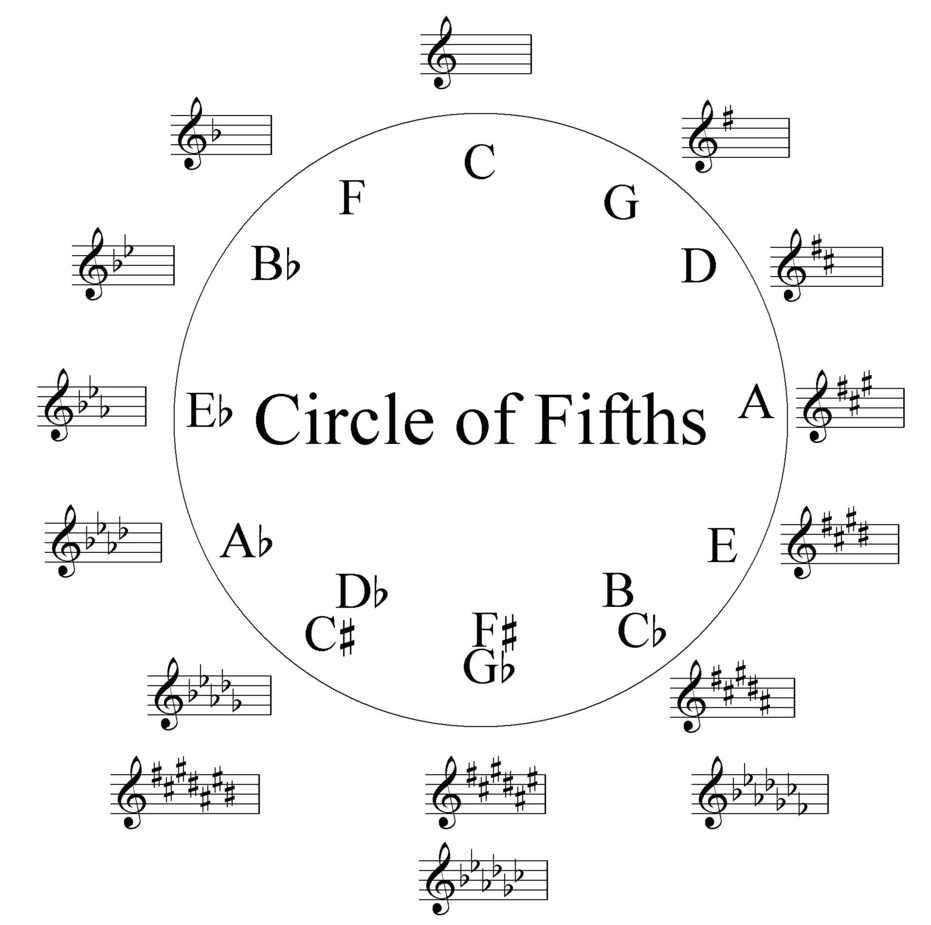
Очень часто мажорные тональности изображают на внешней части квинтового круга, а минорные - на внутренней.
Итан Хейн (англ.
Итан Хейн ), профессор музыки Государственного университета Монклера, говорит что кружок помогает понять структуру западной музыки разных стилей: классического рока, фолк-рока, поп-рока и джаза.
«Большинство западных слушателей будут воспринимать тональности и аккорды, расположенные близко друг к другу в квинтовом круге.
Тональности ля мажор и ре мажор содержат по шесть одинаковых нот, поэтому переход от одной к другой происходит плавно и не вызывает ощущения диссонанса.
У мажора и ми-бемоль мажора есть только одна общая нота, поэтому переход от одной тональности к другой будет звучать странно или даже неприятно», — объясняет Итан.
Оказывается, с каждым шагом по квинтовому кругу в исходной гамме до мажор один из тонов сменяется другим.
Например, переход от до-мажора к соседнему соль-мажору приводит к замене всего одного тона, а перемещение на пять ступеней от до-мажора к си-мажору приводит к замене пяти тонов в исходной гамме.
Таким образом, чем ближе два данных тона расположены друг к другу, тем ближе степень их родства.
По системе Римского-Корсакова, если между тональностями существует расстояние в один шаг, это первая степень родства, два шага – вторая, три – третья.
К ключам первой степени родства (или просто родственным) относятся те старшие и младшие, которые отличаются от исходного ключа одним знаком.
Ко второй степени родства относятся тональности, родственные родственным тональностям.
Точно так же тональности третьей степени родства являются тональностями первой степени родства с тональностями второй степени родства.
Именно степень родства объясняет, почему эти две последовательности аккордов часто используются в поп-музыке и джазе:
- Е7, А7, Д7, Г7, С
«В джазе тональность обычно меняется по часовой стрелке, а в роке, фолке и кантри — против часовой стрелки», — говорит Итан.Появление пятый круг было связано с тем, что музыкантам требовалась универсальная схема, которая позволяла бы быстро определять взаимосвязи тональностей и аккордов.
«Если вы поймете, как устроен квинтовый круг, вы без труда сможете играть в выбранной вами тональности — вам не придется изо всех сил стараться найти нужные ноты», — заключает Гейл Грейс.
Теги: #Научно-популярная #аудиомания #Звук #Логические игры #мозг #музыкальная теория #теория музыки
-
Telegram-Бот Для Сложных Квестов
19 Oct, 24 -
Опыт Поиска Работы На Бирже Elance
19 Oct, 24 -
Как Отправить Отзыв Об Ie8
19 Oct, 24 -
Виста В Десятке... Худшая!
19 Oct, 24


