Содержание курса
- Статья 1: Алгоритм Брезенхема
- Статья 2: растеризация треугольников + обрезка заднего края
- Статья 3: Удаление невидимых поверхностей: z-буфер
- Статья 4: Необходимая геометрия: фестиваль матриц
- 4а: Создание искажения перспективы
- 4б: перемещение камеры и что из этого следует
- 4c: новый растеризатор и исправление перспективных искажений
- Статья 5: Пишем шейдеры для нашей библиотеки
- Статья 6. Немного больше, чем просто шейдер: рендеринг теней
Улучшение кода
Статья 3.1: Пришло время рефакторинга Статья 3.14: Красивый класс матрицОфициальный перевод (с небольшой доработкой) доступен.
Сегодня мы заканчиваем обучающий урок по геометрии, в следующий раз будет весело с шейдерами! Чтобы не совсем скучно, вот оттенок Гуро:

Я удалил текстуры, чтобы было понятнее.
Колеровка по Гуро очень просто: добрый коллега-моделист дал нам векторы нормалей для каждой вершины объекта, они хранятся в строках vn x y z файла .
obj. Мы подсчитываем интенсивность света для каждой вершины треугольника и просто интерполируем интенсивность внутри.
Точно так же, как мы это делали для глубины z или для текстурных координат uv! Кстати, если бы моделист не был так добр, мы могли бы посчитать нормали к вершине как среднее нормалей граней, прилегающих к этой вершине.
Текущий код, сгенерировавший это изображение, находится Здесь .
Ликбез: изменение основы в трехмерном пространстве В евклидовом пространстве система координат (точка отсчета) задается точкой отсчета и основой пространства.
Что означает, что в системе координат (O, i,j,k) точка P имеет координаты (x,y,z)? Это означает, что вектор OP задается следующим образом:
Теперь представьте, что у нас есть второй кадр (O',i',j',k').
Как преобразовать координаты точки, заданные в одном тесте, в другой тест? Для начала заметим, что поскольку (i,j,k) и (i',j',k') являются базисами, существует невырожденная матрица M такая, что:
Давайте нарисуем иллюстрацию, чтобы было понятнее: 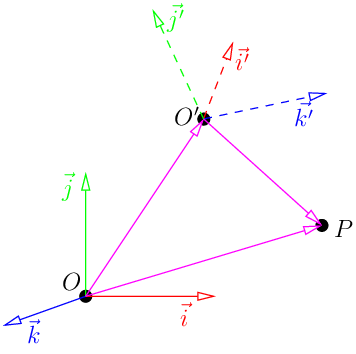
Запишем представление вектора ОП:
Подставим во вторую часть выражение замены базиса:
И это даст нам формулу замены координат для двух баз.
Напишите свой gluLookAt OpenGL и, как следствие, наш маленький рендерер умеет рисовать сцены только с камерой, расположенной по оси z .
Если нам понадобится переместить камеру, ничего страшного, мы просто переместим всю сцену, оставив камеру неподвижной.
Поставим задачу так: мы хотим убедиться, что камера находится в точке е (глаз), посмотрел в точку с (в центре) и так, чтобы заданный вектор ты (вверх) будет вертикальным на нашем окончательном изображении.
Вот иллюстрация: 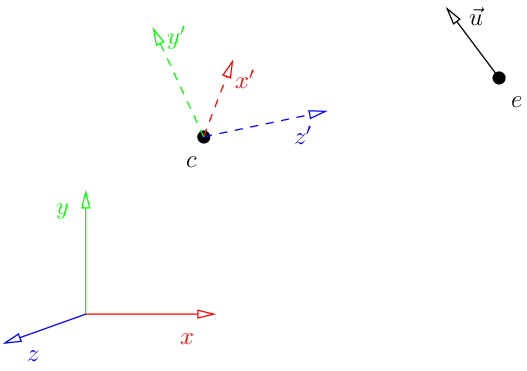
Это просто означает, что мы визуализируемся в контрольную точку (c, x'y'z').
Но модель задана в кадре (O,xyz), а это значит, что нам нужно вычислить кадр x'y'z' и соответствующую матрицу перехода.
Вот код, который возвращает нужную нам матрицу: обновлять: Будьте внимательны, код в репозитории неверный, код приведенный здесь правильный
screen_coords[j] = Vec2i((v.x+1.)*width/2., (v.y+1.)*height/2.);Начнем с того, что z’ — это просто вектор CE (не забудем нормализовать, так проще работать).
Как вычислить х'? Просто векторное произведение между ты И з' .
Затем вычисляем y', который будет ортогонален уже вычисленным x' и z' (напоминаю, что по условиям задачи вектор CE И ты не обязательно ортогонально).
Самым последним аккордом делаем параллельный перенос на с , и наша матрица пересчета координат готова.
Достаточно взять любую точку с координатами (x,y,z,1) в старом базисе, умножить ее на эту матрицу, и мы получим координаты в новом базисе! В OpenGL эта матрица называется матрицей представления.
Область просмотра Если помните, я встречал в своем коде подобные конструкции:
Matrix viewport(int x, int y, int w, int h) {
Matrix m = Matrix::identity(4);
m[0][3] = x+w/2.f;
m[1][3] = y+h/2.f;
m[2][3] = depth/2.f;
m[0][0] = w/2.f;
m[1][1] = h/2.f;
m[2][2] = depth/2.f;
return m;
}
Что это значит? У меня есть точка Vec2f v, принадлежащая квадрату [-1,1]*[-1,1].
Я хочу нарисовать его на картинке с размерами (ширина, высота).
Вектор (v.x+1) изменяется от 0 до 2, (v.x+1.)/2. от нуля до единицы, ну (v.x+1.)*width/2. закрывает всю картину, а это то, что мне нужно.
Но мы переходим к матричному представлению аффинных карт, поэтому давайте посмотрим на следующий код:
Viewport * Projection * View * Model * v.Он строит эту матрицу:
Это означает, что куб мировых координат [-1,1]*[-1,1]*[-1,1] отображается в куб экранных координат (да, куб, поскольку у нас есть z-буфер!) [ x,x+w]*[y,y+h]*[0,d], где d — разрешение z-буфера (у меня 255, потому что я храню его непосредственно в черно-белом изображении).
В мире OpenGL эта матрица называется матрицей области просмотра.
Цепочка преобразований Итак, подведем итоги.
Модели (например, персонажи) выполняются в собственной локальной системе координат (координатах объекта).
Они вставляются в сцену, которая выражается в мировых координатах.
Переход от одного к другому осуществляется матрицей Модели.
Далее мы хотим выразить это в привязке камеры (координатах глаза), матрица перехода от мира к камере называется View. Затем проводим искажение перспективы с помощью Матрицы проекции (см.
статью 4а), она преобразует сцену в так называемые координаты клипа.
Ну а потом выводим все это дело на экран, матрица перехода к координатам экрана — Viewport. То есть, если мы читаем точку v из файла, то чтобы показать ее на экране, мы выполняем умножение
Vec3f v = model->vert(face[j]); screen_coords[j] = Vec3f(ViewPort*Projection*ModelView*Matrix(v));Если вы заглянете код на гитхабе , то мы увидим следующие строки:
void lookat(Vec3f eye, Vec3f center, Vec3f up) {
Vec3f z = (eye-center).
normalize();
Vec3f x = cross(up,z).
normalize();
Vec3f y = cross(z,x).
normalize();
Matrix Minv = Matrix::identity();
Matrix Tr = Matrix::identity();
for (int i=0; i<3; i++) {
Minv[0][i] = x[i];
Minv[1][i] = y[i];
Minv[2][i] = z[i];
Tr[i][3] = -center[i];
}
ModelView = Minv*Tr;
}
Поскольку я рисую только один объект, моя матрица Модели просто одна, я объединил ее с матрицей Вида.
Преобразование нормальных векторов Широко известен следующий факт: Если мы имеем данную модель и уже вычислили (или, например, указали вручную) векторы нормалей к этой модели, и эта модель подвергнута (аффинному) преобразованию M, то векторы нормалей подлежат преобразованию, обратному преобразованию транспонированный М.
Извините, что?! Этот момент для многих остается волшебным, но на самом деле ничего волшебного здесь нет. Рассмотрим треугольник и вектор а , что нормально к его наклонной грани.
Если мы просто растянем наше пространство дважды по вертикали, то преобразованный вектор а перестанет быть нормальным для преобразившегося лица.
Чтобы убрать всю магию, нужно понять одну простую вещь: нам нужно не просто преобразовать векторы нормалей, нам нужно вычислить векторы нормалей для преобразованной модели.
Итак, у нас есть нормальный вектор а =(А,В,С).
Мы знаем, что плоскость, проходящая через начало координат и имеющая вектор нормали а (на нашей иллюстрации это наклонная грань левого треугольника), задается уравнением Ax+By+Cz=0. Запишем это уравнение в матричной форме, причем сразу в однородных координатах:
Напомню, что (A,B,C) — вектор, поэтому при погружении в четырехмерное пространство он получает ноль в последней компоненте, а (x,y,z) — точка, поэтому мы присваиваем 1 это.
Давайте добавим единичную матрицу (M, умноженную на ее обратную) в середину этого обозначения:
Выражение в правых скобках — это преобразованные точки.
Слева нормальный вектор! Поскольку в стандартном соглашении о линейном отображении мы записываем векторы (и точки) в столбце (надеюсь, мы не затеем холивару о ко- и контравариантных векторах), предыдущее выражение можно записать следующим образом:
Что как раз и приводит нас к упомянутому выше факту, что нормаль к преобразованному объекту получается преобразованием исходной нормали, обратной транспонированной М.
Обратите внимание, что если M представляет собой композицию параллельных перемещений, вращений и равномерных растяжений, то транспонированное M равно обратному M, и они компенсируют друг друга.
Но поскольку наши матрицы преобразования будут включать в себя искажения перспективы, это нам не сильно поможет. В текущем коде мы не используем обычное преобразование, но в следующей статье о шейдерах это будет очень важно.
Приятного программирования! Теги: #геометрия для пятого класса #геометрия для пятого класса #штриховка по Гуро #штриховка гуро #программирование #разработка игр

-
Вам Нужно Написать Прямо Сейчас!
19 Oct, 24 -
Закон Яровой – Оценки С Другой Стороны
19 Oct, 24 -
Карьера Программиста. Часть 3. Университет
19 Oct, 24 -
Редкий Моноблок Compaq Presario 3020
19 Oct, 24 -
Онлайн-Трансляция Дроидкона Москва 2015
19 Oct, 24 -
Удаленный Доступ К Ide С Помощью Projector
19 Oct, 24 -
Руководство По Power Bi: Начало Работы
19 Oct, 24


