Исследовательская работа – пожалуй, самая интересная часть нашего обучения.
Идея состоит в том, чтобы еще во время учебы в университете попробовать себя в выбранном направлении.
Например, студенты направлений «Программная инженерия» и «Машинное обучение» часто едут заниматься исследованиями в компании (в основном JetBrains или Яндекс, но не только).
В этом посте я расскажу о своем проекте в области компьютерных наук.
В рамках своей работы я изучал и применял на практике подходы к решению одной из самых известных NP-трудных задач: проблема покрытия вершин .
В настоящее время очень быстро развивается интересный подход к решению NP-трудных задач — параметризованные алгоритмы.
Я постараюсь ввести вас в курс дела, рассказать вам несколько простых параметризованных алгоритмов и описать один мощный метод, который мне очень помог.
Я представил свои результаты на конкурсе PACE Challenge: по результатам открытых тестов мое решение занимает третье место, а окончательные результаты будут известны 1 июля.

Обо мне
Меня зовут Василий Алферов, я сейчас заканчиваю третий курс Высшей школы экономики? - Санкт-Петербург.Алгоритмами я интересуюсь еще со школьной скамьи, когда учился в московской школе № 179 и успешно участвовал в олимпиадах по информатике.
В бар входит конечное число специалистов по параметризованным алгоритмам.
Пример взят из книги «Параметризованные алгоритмы» Представьте, что вы охранник бара в маленьком городке.
Каждую пятницу к вам в бар приходит отдохнуть полгорода, что доставляет вам массу хлопот: вам нужно выкидывать из бара дебоширных клиентов, чтобы предотвратить драки.
В конце концов вам это надоест, и вы решите принять профилактические меры.
Поскольку ваш город небольшой, вы точно знаете, какие пары посетителей могут подраться, если окажутся вместе в баре.
У вас есть список н люди, которые придут в бар сегодня вечером.
Вы решаете не допустить некоторых горожан в бар, чтобы никто не ввязался в драку.
В то же время ваше начальство не хочет терять прибыль и будет недовольно, если вы не допустите больше, чем к Человек.
К сожалению, перед вами стоит классическая NP-трудная задача.
Возможно, вы знаете ее как Крышка вершины или как задача о покрытии вершин.
Для таких задач в общем случае не существует алгоритмов, работающих за приемлемое время.
Если быть точным, то недоказанная и довольно сильная гипотеза ETH (Exponential Time Hypothesis) говорит о том, что эту проблему невозможно решить за время.
, то есть ничего заметно лучше, чем полный перебор, не придумаешь.
Например, предположим, что кто-то собирается прийти к вам в бар.
п = 1000 Человек.
Тогда полный поиск будет
вариантов, которые есть примерно
- сумасшедшая сумма.
К счастью, ваше руководство наложило на вас ограничения.
к = 10 , поэтому количество комбинаций, которые вам нужно перебрать, намного меньше: количество подмножеств из десяти элементов равно
.
Так уже лучше, но за день все равно не посчитаешь даже на мощном кластере.

Чтобы исключить возможность драки в такой конфигурации натянутых отношений между посетителями бара, нужно не пускать Боба, Дэниела и Федора.
Не существует решения, при котором останутся только двое.
Означает ли это, что пришло время сдаться и впустить всех? Давайте рассмотрим другие варианты.
Ну, например, нельзя пускать только тех, кто, скорее всего, будет драться с очень большим количеством людей.
Если кто-то может сражаться хотя бы с к+1 другого человека, то его точно нельзя пускать - иначе придется всех не пускать к+1 горожане, с которыми он может сражаться, что обязательно расстроит руководство.
Пусть по этому принципу выкидываете всех, кого можно.
Тогда все остальные смогут сражаться, используя не более к люди.
Выбрасывая их к чувак, ты не можешь предотвратить ничего, кроме
конфликты.
Это означает, что если имеется более
Если человек вовлечен хотя бы в один конфликт, то предотвратить их все вы уж точно не сможете.
Так как, конечно, вы обязательно впустите совершенно неконфликтных людей, то вам нужно пройти все подгруппы размером десять человек из двухсот. Есть примерно
, и это количество операций уже можно перебрать на кластере.
Если можно смело брать особей, у которых вообще нет конфликта, то как быть с теми, кто участвует только в одном конфликте? Фактически, их также можно впустить, закрыв дверь перед противником.
Действительно, если Алиса конфликтует только с Бобом, то если мы выпустим Алису из них двоих, мы не проиграем: у Боба могут быть и другие конфликты, но у Алисы их точно нет. Более того, нам не имеет смысла не пускать нас обоих.
После таких операций не остается больше
гости с нерешенной судьбой: у нас есть только
конфликты, каждый из которых имеет двух участников и каждый вовлечен как минимум в два.
Так что остается только разобраться
варианты, которые легко можно рассматривать полдня на ноутбуке.
На самом деле, простыми рассуждениями можно добиться еще более привлекательных условий.
Заметим, что нам обязательно нужно разрешить все споры, то есть из каждой конфликтующей пары выбрать хотя бы одного человека, которого мы не будем пускать.
Рассмотрим следующий алгоритм: берем любой конфликт, из которого удаляем одного участника и рекурсивно начинаем с остаток, затем удалите другой и также начните рекурсивно.
Поскольку на каждом шаге мы кого-то выбрасываем, дерево рекурсии такого алгоритма представляет собой бинарное дерево глубины.
к , поэтому в целом алгоритм работает в
, Где н - количество вершин, а м - количество ребер.
В нашем примере это около десяти миллионов, которые можно посчитать за доли секунды не только на ноутбуке, но даже на мобильном телефоне.
Приведенный выше пример является примером параметризованный алгоритм .
Параметризованные алгоритмы — это алгоритмы, которые выполняются во времени.
f(k) поли(n) , Где п - полиномиальный, ж — произвольная вычислимая функция, и к - некий параметр, который, вполне возможно, будет намного меньше размера задачи.
Все рассуждения перед этим алгоритмом приведены на примере кернеризация — один из общих методов создания параметризованных алгоритмов.
Кернелизация — это уменьшение размера задачи до значения, ограниченного функцией параметра.
Возникающую проблему часто называют ядром.
Таким образом, путем несложных рассуждений о степенях вершин мы получили квадратичное ядро задачи Vertex Cover, параметризованное размером ответа.
Для этой задачи вы можете выбрать и другие настройки (например, «Покрытие вершин над LP»), но именно эту настройку мы и обсудим.
Темп вызова
Соревнование Вызов ПАСЕ (The Parameterized Algorithms and Computational Experiments Challenge) родился в 2015 году с целью установить связь между параметризованными алгоритмами и подходами, используемыми на практике для решения вычислительных задач.Первые три конкурса были посвящены нахождению ширины дерева графа ( Ширина дерева ), поиск дерева Штейнера ( Дерево Штайнера ) и поиск множества вершин, разрезающих циклы ( Набор вершин обратной связи ).
В этом году одной из задач, в решении которой вы могли попробовать свои силы, стала описанная выше задача покрытия вершин.
Конкурс с каждым годом набирает популярность.
Если верить предварительным данным, в этом году в соревновании только по решению задачи вершинного покрытия приняли участие 24 команды.
Стоит отметить, что конкурс длится не несколько часов и даже не неделю, а несколько месяцев.
У команд есть возможность изучить литературу, придумать свою оригинальную идею и попробовать ее реализовать.
По сути, этот конкурс является исследовательским проектом.
Представление наиболее эффективных решений и награждение победителей пройдут приурочено к конференции.
ИПЕК (Международный симпозиум по параметризованным и точным вычислениям) в рамках крупнейшего ежегодного алгоритмического собрания в Европе АЛГО .
Более подробную информацию о самом конкурсе можно найти на сайте Веб-сайт , а результаты прошлых лет лежат здесь .
Схема решения
Чтобы решить проблему покрытия вершин, я попробовал использовать параметризованные алгоритмы.Обычно они состоят из двух частей: правил упрощения (которые в идеале приводят к кернеризации) и правил разделения.
Правила упрощения — это предварительная обработка входных данных за полиномиальное время.
Цель применения таких правил — свести проблему к эквивалентной меньшей проблеме.
Правила упрощения — самая затратная часть алгоритма, и применение этой части приводит к общему времени работы.
вместо простого полиномиального времени.
В нашем случае правила разбиения основаны на том, что для каждой вершины в качестве ответа нужно взять либо ее, либо ее соседа.
Общая схема такая: применяем правила упрощения, затем выбираем какую-то вершину и делаем два рекурсивных вызова: в первом берем ее в ответ, а во втором берем всех ее соседей.
Это то, что мы называем расщеплением (ветвлением) по этой вершине.
В следующем параграфе к этой схеме будет сделано ровно одно дополнение.
Идеи для правил разделения (бранчей)
Обсудим, как выбрать вершину, по которой будет происходить расщепление.Основная идея очень жадная в алгоритмическом смысле: возьмем вершину максимальной степени и разобьем по ней.
Почему это кажется лучше? Потому что во второй ветке рекурсивного вызова мы таким образом удалим много вершин.
Вы можете рассчитывать на то, что останется небольшой график, и мы сможем быстро над ним поработать.
Этот подход вместе с уже рассмотренными простыми приемами кернеризации хорошо показывает себя и решает некоторые тесты размером в несколько тысяч вершин.
Но, например, это плохо работает для кубических графов (то есть графов, у которых степень каждой вершины равна трем).
Есть еще одна идея, основанная на довольно простой идее: если граф несвязен, задачу о его компонентах связности можно решить самостоятельно, объединив в конце ответы.
Это, кстати, небольшая обещанная модификация схемы, которая существенно ускорит решение: раньше в этом случае мы работали на произведение времен расчета откликов компонентов, а теперь работаем на сумма.
А чтобы ускорить ветвление, нужно превратить связный граф в несвязный.
Как это сделать? Если в графике есть точка артикуляции, за нее нужно бороться.
Точка сочленения — это вершина, при удалении которой граф теряет связность.
Все точки соединения в графе можно найти с помощью классического алгоритма за линейное время.
Такой подход значительно ускоряет ветвление.
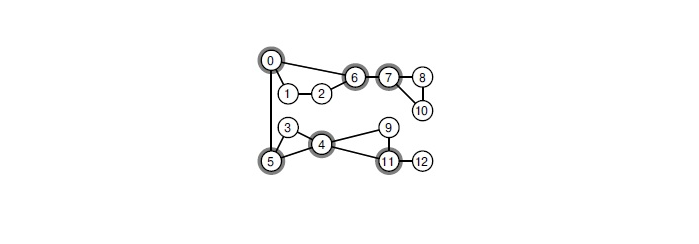
При удалении любой из выбранных вершин граф разбивается на компоненты связности.
Мы сделаем это, но мы хотим большего.
Например, найдите в графе небольшие разрезы вершин и разделите его по вершинам.
Самый эффективный из известных мне способов найти минимальное глобальное сокращение вершин — использовать дерево Гомори-Ху, построенное за кубическое время.
В PACE Challenge типичный размер графа составляет несколько тысяч вершин.
В этой ситуации необходимо выполнить миллиарды операций в каждой вершине дерева рекурсии.
Оказывается, решить проблему за отведенное время просто невозможно.
Попробуем оптимизировать решение.
Минимальный вершинный разрез между парой вершин можно найти с помощью любого алгоритма, создающего максимальный поток.
Вы можете пустить его в такую сеть Алгоритм Диница , на практике это работает очень быстро.
У меня есть подозрение, что теоретически можно доказать оценку времени работы
, что уже вполне приемлемо.
Я несколько раз пробовал искать разрезы между парами случайных вершин и брать наиболее сбалансированную.
К сожалению, это привело к плохим результатам в открытом тестировании PACE Challenge. Я сравнил его с алгоритмом, который разбивает вершины максимальной степени, запуская их с ограничением глубины спуска.
После того, как алгоритм попытался найти разрез таким образом, остались графы большего размера.
Это связано с тем, что разрезы получились очень несбалансированными: удалив 5-10 вершин, можно было отколоть только 15-20. Стоит отметить, что в статьях о теоретически самых быстрых алгоритмах используются гораздо более продвинутые методы выбора вершин для разделения.
Такие методы имеют очень сложную реализацию и зачастую низкую производительность с точки зрения времени и памяти.
Мне не удалось выделить те, которые вполне приемлемы для практики.
Как применять правила упрощения
У нас уже есть идеи по кернеризации.Позвольте мне напомнить вам:
- Если есть изолированная вершина, удалите ее.
- Если есть вершина степени 1, удаляем ее и в ответ берем ее соседа.
- Если существует вершина степени не ниже к+1 , забери это обратно.
Если в шуточной задаче о баре нам дали верхний предел к , то в PACE Challenge вам просто нужно найти вершинное покрытие минимального размера.
Это типичное преобразование задач поиска в задачи принятия решений; часто нет никакой разницы между двумя типами проблем.
На практике, если мы пишем решатель задачи покрытия вершин, может быть разница.
Например, как в третьем пункте.
С точки зрения реализации есть два пути.
Первый подход называется итеративным углублением.
Он заключается в следующем: мы можем начать с некоторого разумного ограничения снизу на ответ, а затем запустить наш алгоритм, используя это ограничение в качестве ограничения на ответ сверху, не опускаясь в рекурсии ниже этого ограничения.
Если мы нашли какой-то ответ, то он гарантированно будет оптимальным, иначе мы можем увеличить этот предел на единицу и начать заново.
Другой подход заключается в сохранении некоторого текущего оптимального ответа и поиске меньшего ответа, изменяя этот параметр при его обнаружении.
к для большего отсечения ненужных ветвей при поиске.
Проведя несколько ночных экспериментов, я остановился на сочетании этих двух методов: сначала я запускаю свой алгоритм с каким-то ограничением глубины поиска (выбирая его так, чтобы оно занимало ничтожно малое время по сравнению с основным решением) и использую лучший решение найдено как верхняя граница ответа - то есть к одному и тому же к .
Вершины степени 2
Мы разобрались с вершинами степени 0 и 1. Оказывается, это можно сделать и с вершинами степени 2, но это потребует более сложных операций со стороны графа.Чтобы это объяснить, нам нужно как-то обозначить вершины.
Назовем вершину степени 2 вершиной в , и его соседи - вершины Икс И й .
Дальше у нас будет два случая.
- Когда Икс И й - соседи.
Тогда ты сможешь ответить Икс И й , А в удалить.
Ведь из этого треугольника нужно взять взамен хотя бы две вершины, и мы точно не проиграем, если возьмем Икс И й : у них наверняка есть другие соседи, и в Их нет.
- Когда Икс И й - не соседи.
Тогда утверждается, что все три вершины можно склеить в одну.
Идея состоит в том, что в этом случае существует оптимальный ответ, при котором мы берем либо в , или обе вершины Икс И й .
Причем в первом случае нам придется брать в ответ всех соседей Икс И й , но во втором это не нужно.
Это как раз соответствует случаям, когда мы не берем в ответ склеенную вершину, а когда берем.
Остается лишь заметить, что в обоих случаях отклик от такой операции уменьшается на единицу.
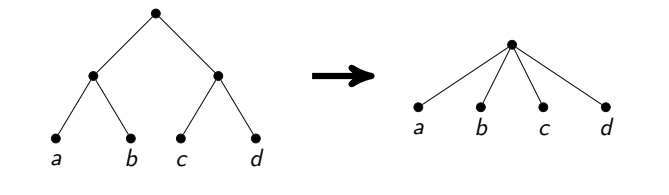
Стоит отметить, что этот подход довольно сложно точно реализовать за достаточно линейное время.
Склеивание вершин — сложная операция; вам нужно скопировать списки соседей.
Если это сделать небрежно, то можно получить асимптотически неоптимальное время работы (например, если копировать много ребер после каждой склейки).
Я остановился на поиске целых путей из вершин степени 2 и анализе кучи частных случаев, таких как циклы из таких вершин или из всех таких вершин, кроме одной.
Кроме того, необходимо, чтобы эта операция была обратимой, чтобы при выходе из рекурсии мы восстанавливали граф в исходный вид. Чтобы гарантировать это, я не очищал списки ребер объединенных вершин, а затем просто знал, какие ребра куда нужно пройти.
Такая реализация графиков также требует точности, но обеспечивает достаточно линейное время.
А для графов с несколькими десятками тысяч ребер он умещается в кэш процессора, что дает большие преимущества в скорости.
Линейное ядро
Наконец, самая интересная часть ядра.
Для начала напомним, что в двудольных графах минимальное вершинное покрытие можно найти с помощью
.
Для этого нужно воспользоваться алгоритмом Хопкрофт-Карп чтобы найти там максимальное паросочетание, а затем воспользоваться теоремой Кениг-Шгервари .
Идея линейного ядра такова: сначала мы раздваиваем граф, то есть вместо каждой вершины в давайте добавим две вершины
И
, и вместо каждого ребра ты - в давайте добавим два ребра
И
.
Полученный граф будет двудольным.
Найдем в нем минимальное вершинное покрытие.
Некоторые вершины исходного графа попадут туда дважды, некоторые — только один раз, а некоторые — никогда.
Теорема Немхаузера-Троттера утверждает, что в этом случае можно удалить вершины, которые не попали ни разу, и вернуть обратно те, которые попали дважды.
Более того, она говорит, что из оставшихся вершин (тех, что попали один раз) нужно взять в качестве ответа хотя бы половину.
Мы только что научились оставлять не более 2 тыс.
вершины Действительно, если остаток ответа составляет не менее половины всех вершин, то всего вершин не больше, чем 2 тыс.
.
Здесь я смог сделать небольшой шаг вперед. Понятно, что построенное таким образом ядро зависит от того, какое минимальное вершинное покрытие мы взяли в двудольном графе.
Хотелось бы взять такой, чтобы количество оставшихся вершин было минимальным.
Раньше они могли это сделать только вовремя
.
Я придумал реализацию этого алгоритма в то время
, таким образом, это ядро можно искать в графах из сотен тысяч вершин на каждом этапе ветвления.
Результат
Практика показывает, что мое решение хорошо работает на тестах из нескольких сотен вершин и нескольких тысяч ребер.В таких тестах вполне можно рассчитывать, что решение будет найдено за полчаса.
Вероятность найти ответ за приемлемое время в принципе возрастает, если граф имеет достаточно большое количество вершин высокой степени, например, степени 10 и выше.
Для участия в конкурсе решения необходимо было прислать на адрес optil.io .
Судя по представленной там информации знак , моё решение в открытых тестах занимает третье место из двадцати, с большим отрывом от второго.
Если быть до конца честным, не совсем понятно, как решения будут оцениваться на самом конкурсе: например, мое решение проходит меньше тестов, чем решение, занявшее четвертое место, но на тех, которые проходят, оно работает быстрее.
Результаты закрытых испытаний станут известны 1 июля.
Теги: #математика #Алгоритмы #программирование #Образовательный процесс в ИТ #ВШ? #ВШ? #СПб.
Петербургская башня #параметризованные алгоритмы #NP-сложные задачи #задача о покрытии вершин #Vertex Cover

-
«Тайный Санта» Для Стартапов
19 Oct, 24 -
История Львиноголовки
19 Oct, 24 -
Чему И Как Учиться, Чтобы Стать Менеджером?
19 Oct, 24


