Цель данной статьи — поделиться результатами исследования по выявлению коинтегрированных пар акций, котирующихся на Московской и Нью-Йоркской биржах, с использованием теста Энгла-Грейнджера.
Если мы возьмем две акции со стационарными приращениями , и мы находим некоторую их линейную комбинацию (разброс), которая будет стационарной, то такой временной ряд будем называть коинтегрированным.
Наличие коинтеграции дает нам возможность хеджироваться акциями и строить рыночно-нейтральную стратегию.
Почему это возможно?
Принцип, на котором основано получение прибыли
Мы все знаем, что цена акции, рассматриваемая как временной ряд, может меняться весьма существенно.Если мы откроем позицию по какой-либо одной бумаге, то в большинстве случаев это будет очень рискованная игра, поскольку мы возьмем на себя все риски, связанные с ее волатильностью.
Однако есть акции, от которых можно ожидать, что при объединении в пару аналогичные серии не будут слишком далеко отходить друг от друга.
Эта концепция называется долгосрочным динамическим равновесием.
В условиях стационарности долгосрочное динамическое равновесие приобретает более точную форму.
Если мы возьмем стационарный ряд спреда, построенный между двумя коинтегрированными ценными бумагами, он будет иметь свойство возвращаться к среднему значению, то есть при любом отклонении от некоторого равновесия он будет стремиться вернуться обратно.
На этом принципе строится рыночно-нейтральная стратегия.
Как найти пары, связанные с долгосрочным динамическим равновесием на фондовых рынках?
Корреляция
Первая мысль, которая приходит в голову, — вычислить корреляцию между двумя ценными бумагами и торговыми парами с сильной корреляцией.Этот подход неэффективен по двум причинам.
Во-первых, если бы ценовые ряды двух акций были идеально коррелированы, то есть если бы они двигались в одном направлении и в одной и той же пропорции, разница между рядами была бы равна нулю, и мы не смогли бы заработать никаких денег.
деньги, потому что ни одна акция никогда не будет слишком дорогой или слишком дешевой.
Во-вторых, корреляция мало что говорит нам об отношениях между двумя акциями в долгосрочной перспективе.
Например, возьмем большой и диверсифицированный портфель акций.
Пусть эти акции также будут включены в фондовый индекс и пусть вес акций в портфеле определяется их весами в индексе.
Хотя портфель должен двигаться в соответствии с индексом в долгосрочной перспективе, будут периоды, когда акции, входящие в индекс, но не входящие в портфель, будут иметь необычные движения цен.
Следовательно, эмпирические корреляции между портфелем и индексом в течение некоторого времени могут быть довольно низкими.
Из-за этого при анализе мы просто отбросим такой портфель и упустим возможность заработать.
Отсюда следует, что корреляция не является хорошим способом идентификации пар.
Для идентификации пар лучше использовать коинтеграцию.
Коинтеграция
Часто для обеспечения стационарности экономического ряда мы принимаем разности.Это приводит к следующему определению интеграции.
Временной ряд называется интегрированным порядком.
и обозначен
, если оно и его различия соответствуют порядку
включительно нестационарна, и ее разность имеет порядок
стационарный.
Для получения практических результатов нам нужны только значения
И
.
Если
, то сам ряд будет стационарным, и для краткости я буду далее обозначать такие ряды
.
Для
будет скандал нестационарный со стационарными приращениями (разности первого порядка), и для краткости далее я буду обозначать такие ряды
.
Пусть у нас будет два
ряд,
И
.
Пусть, кроме того, их линейная комбинация
является
В этом случае строки
И
называются коинтегрированными:
По сути, коинтеграция — это регрессия нестационарных рядов.
Это означает, что если
имеет нулевое среднее, то этот ряд редко будет отклоняться далеко от нуля и часто пересекает нулевой уровень.
Другими словами, время от времени будет достигаться точное равновесие или что-то близкое к нему.
Коинтеграция логарифмов цен
Мы можем рассматривать коинтеграцию не только между ценами, но и между их логарифмами.К сожалению, коинтеграция логарифмов цен двух акций менее очевидна и интуитивна, чем простая коинтеграция цен двух акций.
Однако почему коинтеграция возможна в случае логарифмов? Это объясняется «гипотезой эффективного рынка», моделью ценообразования опционов и леммой Ито.
На самом деле гипотеза эффективного рынка не имеет строгой формализации.
Эта гипотеза предполагает, что на ликвидном рынке, где цена актива будет результатом сбалансированного спонтанного спроса и предложения, текущая цена будет точно отражать всю информацию, доступную игрокам на рынке.
Будущие изменения цен могут быть только результатом «новостей», которые по определению непредсказуемы, поэтому лучший прогноз цен на любую будущую дату — это просто цена сегодня.
Другими словами, сегодняшняя цена — это вчерашняя цена плюс случайный элемент. Гипотеза эффективного рынка связана с базовой моделью ценообразования опционов.
Фундаментальное предположение этой модели заключается в том, что цена базового актива
удовлетворяет процессу геометрического броуновского движения (GBM):
Где
И
являются константами, которые представляют, соответственно, смещение цены актива и волатильность доходности, и
является винеровским процессом, то есть приращением
независимы и нормально распределены с нулевым средним значением и дисперсией
.
Чтобы увидеть, как уравнение GBM связано с гипотезой эффективного рынка, нам нужно применить к нему лемму Ито.
Что это такое? Предположим, что значения переменной
подчиняются стохастическому дифференциальному уравнению (СДУ)
Где
является винеровским процессом, и
И
– функции, зависящие от переменных
И
.
Предположим также, что функция
зависит от переменных
И
и имеет производные
,
,
.
Лемма Ито утверждает, что эта функция подчиняется уравнению
По сути, лемма Ито представляет собой формулу замены переменных в СДУ, где при определенных условиях функция некоторой СДУ также является СДУ.
Вернемся к уравнению ГБМ и преобразуем его к виду
Веруя
, по лемме Ито получаем:
Давайте представим функцию
.
Поскольку
мы получаем:
Уравнение
можно переписать в дискретной форме
Где
, А
, то есть вот этот процесс
не просто стационарен, а представляет собой белый шум.
Понятие стационарного процесса шире, чем белый шум, и отличается тем, что стационарный процесс имеет постоянное математическое ожидание, но оно не обязательно должно быть равно нулю, как в случае с белым шумом.
Дискретную версию приведенного выше уравнения, в свою очередь, можно записать как:
Это уравнение представляет собой модель случайного блуждания (RW), которая обычно используется для моделирования логарифмов цен на эффективных финансовых рынках и является примером
процесс.
Таким образом, коинтеграция может также применяться к логарифмам цен на акции.
Хотя некоторые скептики (в частности я) могут сомневаться в адекватности описания цен на акции уравнением GBM и, следовательно, в способности коинтегрировать логарифмы цен, эмпирические данные успешно развеяли этот скептицизм.
Я проверил: если цены коинтегрированы, то и их логарифмы коинтегрированы.
Коинтеграционное тестирование
Роберт Энгл и Клайв Грейнджер были первыми, кто придумал метод тестирования коинтеграции.В 2003 году они получили Нобелевскую премию по экономике за разработку метода коинтеграции для анализа временных рядов.
Они описали это за 15 лет до награждения, в 1987 году, в статье «Коинтеграция и исправление ошибок: представление, оценка и тестирование».
Концептуально, чтобы на основе имеющихся наблюдений определить, являются ли временные ряды
И
коинтегрированы, нам нужно проверить нулевую гипотезу
из-за отсутствия коинтеграции между сериями
И
против альтернативной гипотезы
.
Если нулевая гипотеза отвергается, принимается наличие коинтеграции.
Оригинальный тест на коинтеграцию был назван тестом Энгла-Грейнджера в честь его создателей.
Это двухэтапный процесс, которому предшествует проверка.
И
для интегрируемости первого порядка,
И
.
Подробно об этом мы говорили в статье о стационарных приращениях .
По сути, здесь описаны все подготовительные работы, которые необходимо провести перед тем, как приступить непосредственно к тесту Энгла-Грейнджера.
Допустим, мы сделали это.
Строки
И
коинтегрированы, если их распространение
, то есть он стационарен.
Первым шагом в тесте Энгла-Грейнджера является получение непротиворечивой оценки.
.
Это делается путем применения линейной регрессии МНК (наименьших квадратов) к уравнению
.
Второй шаг — проверка стационарности остатков.
получено путем МНК-оценки уравнения коинтеграции.
Обычно мы проверяем стационарность с помощью теста Дикки-Фуллера.
Однако в 1990 году Филлипс и Улиарис в своей статье «Асимптотические свойства тестов коинтеграции на основе остатков» показали, что для проверки ряда
тест Дики-Фуллера использовать нельзя.
Дело в том, что OLS «выбирает» остатки так, чтобы они имели минимально возможное изменение, поэтому, даже если переменные не коинтегрированы, OLS делает остатки «выглядящими» как стационарные.
Из-за этого при использовании теста Дики-Фуллера слишком часто отвергается гипотеза нестационарности и, соответственно, ошибочно принимается гипотеза коинтеграции.
Если мы изучим статью авторов, то увидим, что в приложении они приводят таблицы с критическими значениями, но они оказались достаточно неточными.
Позже, в 1991 году, Энгл и Грейнджер опубликовали книгу «Долгосрочные экономические отношения».
В ней, в 13-й главе, озаглавленной «Критическое значение для тестов на коинтеграцию», Маккиннон привел уточненные асимптотические критические значения.
-статистика, полученная путем моделирования и подходящая для данного случая.
В 1993 году Маккиннон и Дэвидсон опубликовали свою книгу «Оценка и вывод в эконометрике», где также представили обновленные критические значения.
Таким образом, если
(остатки стационарны), тогда
(распространение также стационарно), что означает наличие коинтеграции между
И
.
В целом метод Энгла-Грейнджера сводится к следующему:
- оценка
использование MNC; - расчет спреда
и тестирование
для стационарности с использованием уточненных критических значений.
Тестирование коинтеграции в MATLAB
Итак, у нас есть две серии цен на акции:И
.
Мы хотим, чтобы
И
были коинтегрированы, то есть так, что распространение
был стационарным.
Если нам нужен стационарный ряд с нулевым средним значением, мы можем включить в уравнение константу, чтобы разброс выглядел как
.
Начнем с результатов, полученных на Московской бирже, которые я описал в статье.
Там я нашел пять
ряды.
Составим из них все возможные комбинации и проверим на коинтеграцию с помощью теста Энгла-Грейнджера.
Для начала выберем нужные нам ценные бумаги из базы данных Microsoft SQL Server, в которой я храню значения цен акций, разобранные с Московской биржи, и импортирую их в виде массива:
В этом массиве четыре из пяти акций имеют данные за январь за 252 торговых дня.conn = database.ODBCConnection('uXXXXXX.mssql.masterhost.ru', 'uXXXXXX', 'XXXXXXXXXX'); curs = exec(conn, 'SELECT ALL PriceId, StockId, Date, Price FROM StockPrices WHERE StockId IN (52, 55, 67, 75, 162) AND Date >= ''2016-01-01 00:00:00.000'' AND Date < ''2017-01-01 00:00:00.000'''); curs = fetch(curs); data = curs.Data sqlquery = 'SELECT ALL StockId, ShortName, Code FROM Stocks WHERE StockId IN (52, 55, 67, 75, 162)'; curs = exec(conn, sqlquery); curs = fetch(curs); names = curs.Data close(conn);
Однако по одной из акций торги начались только в феврале, поэтому данные доступны только за 215 торговых дней.
Для нас критично, чтобы все акции имели одинаковый ценовой массив, поэтому в таких ситуациях у нас есть два варианта.
Первый вариант — исключить из эксперимента акции с коротким набором цен и использовать как можно больше измерений цен, чтобы получить более точные результаты.
Второй вариант — пожертвовать частью данных и включить все акции ради большей практичности.
Я провёл оба эксперимента, и в данном случае разницы в результатах не было, поэтому просто отсекаем январские данные: dates = unique(datetime(data(:,3)));
% Cut dates array until price of stock with StockId=67 is not empty.
dates(1:37,:) = [];
prices = zeros(length(dates),length(names));
for i = 1:length(names)
% Indexes with current stock's data
indexes = find(cell2mat(data(:,2)) == cell2mat(names(i,1)));
if length(indexes) == 252
indexes(1:37,:) = [];
end
for j=1:length(dates)
% Fill prices according to date
prices(j,i) = cell2mat(data(indexes(j),4));
end
end
Тест Энгла-Грейнджера выполняется с использованием функции egcitest, которая принимает на вход массив временных рядов, в данном случае размером
, Где
— количество торговых дней.
На выходе функция возвращает логическое значение, равное 1, если нулевая гипотеза отвергается в пользу альтернативной, и 0 в противном случае.
Следующая проблема, которую нам нужно решить, — какой запас взять для
, а какой - для
.
Лучше всего попробовать оба варианта, а затем сравнить статистику тестов.
В большинстве случаев наблюдается регресс как вперед, так и назад. Начнем со случая, когда
.
Составим все возможные пары из пяти выявленных
серии и выполнить тест Энгла-Грейнджера как для регрессии с фиктивным термином (по умолчанию), так и без него (задается аргументом «creg» со значением «nc»): isCoint = zeros(length(nchoosek(names(:,1),2)), 3);
k=1;
for i=1:length(names)
for j=i+1:length(names)
if mean(prices(:,i)) < mean(prices(:,j))
isCoint(k,1) = cell2mat(names(j,1));
isCoint(k,2) = cell2mat(names(i,1));
testPrices(:,1) = prices(:,j);
testPrices(:,2) = prices(:,i);
else
isCoint(k,1) = cell2mat(names(i,1));
isCoint(k,2) = cell2mat(names(j,1));
testPrices(:,1) = prices(:,i);
testPrices(:,2) = prices(:,j);
end
isCoint(k,3) = egcitest(testPrices);
isCoint(k,4) = egcitest(testPrices, 'creg', 'nc');
k = k + 1;
end
end
В случае фиктивной регрессии программа дважды отклоняет нулевую гипотезу в пользу альтернативной модели, определяя коинтегрированные пары акций с тиккерами (НХП, ВТРС), (НКХП, ЖИВ).
В случае регрессии без фиктивного члена программа один раз отклоняет нулевую гипотезу в пользу альтернативы, идентифицируя коинтегрированную пару акций с тиккерами (VSYDP, NKHP).
В случае обратной регрессии (
) со свободным участником программа дважды отвергает нулевую гипотезу в пользу альтернативной модели, определяя коинтегрированные пары акций с тиккерами (VTRS, NKHP), (ZHIV, NKHP).
В случае регрессии без фиктивного члена программа четыре раза отклоняет нулевую гипотезу в пользу альтернативной, определяя коинтегрированные пары акций с тиккерами (GRNT, VTRS), (GRNT, VSYDP), (GRNT, ZHIV), ( ГРНТ, НХП).
Давайте оценим значения
И
, которые можно получить как возвращаемые значения функции egcitest, и нарисовать спред: % NKHP and VTRS
indexY = 5;
indexX = 1;
testPrices(:,1) = prices(:,indexY);
testPrices(:,2) = prices(:,indexX);
[h,pValue,stat,cValue,reg1,reg2] = egcitest(testPrices);
alpha = reg1.coeff(1);
beta = reg1.coeff(2);
spread = reg1.res;
plot(dates,spread)
legend(strcat(names(indexY,3),'-',names(indexX,3)));
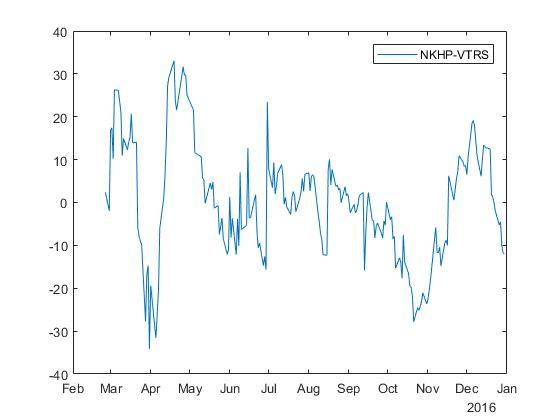
Для акций с тикером НХП и ВТРС получаем спред с коэффициентами
И
: 
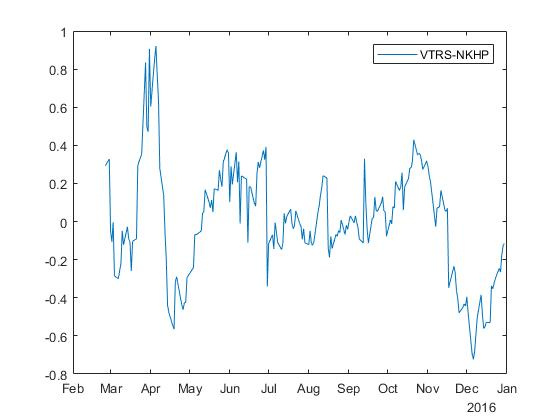
Для обратной регрессии мы получаем «зеркальный» разброс с коэффициентами
И
: 
Для акций с тиккерами НХП и ЖИВ получаем спред с коэффициентами
И
:
Теги: #тест Энгла-Грейнджера #коинтеграция #случайные процессы #анализ временных рядов #регрессия #математика
-
Создание Плана Обучения Emr
19 Oct, 24 -
Стартапы
19 Oct, 24 -
Jelly Bean Портирован На Armv6
19 Oct, 24 -
Как Apple Сливает Информацию
19 Oct, 24 -
Семь Советов, Как Вернуть Интерес К Жизни
19 Oct, 24 -
Интеграция Paypal Here В Приложение Ios
19 Oct, 24


