Статья является продолжением моей первой статьи.
«Фракталы в простых числах» .
Следующая статья: Фракталы в иррациональных числах.
Часть 2 .

В предыдущей статье мы научились рисовать самоподобные закономерности, используя взаимно простые числа.
В этой статье я покажу фрактальную природу числа.
.
Без предисловия.
Под катом.
Определимся с терминологией и обозначениями.
В математике описанные ниже системы называются бильярд .
Мы будем использовать этот термин далее.
Размеры прямоугольного бильярда обозначим через
(ширина) и
(высота).
Бинарный бильярд
В предыдущей статье мы взяли прямоугольный бильярд со сторонамиИ
, запустил в него шарик и обозначил траекторию через ячейку пунктиром:
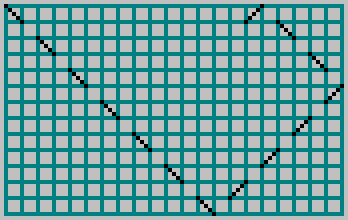
Для относительно простых
И
получаем узор:

В бинарном варианте траекторию отмечаем не пунктиром, а закрашивая ячейки поочередно черным и белым (формируем бинарный массив, в соответствующую ячейку ставим 0 для черного и 1 для белого):

Правила размышлений о границах:

Для относительно простых
И
траектория проходит через каждую ячейку:
Для разных М и N Самое удивительное в этих закономерностях то, что для разных
И
вы получаете свой уникальный узор:




В статье, как
И
, мы используем преимущественно числа Фибоначчи.
Здесь вы можете рисовать шаблоны для других чисел (координат мыши).
Если стороны имеют общий делитель, то мяч попадает в угол, прежде чем пройти через каждый квадрат: 
Этот случай удобно рассматривать как бильярд в прямоугольнике со сторонами
И
(НОД – наибольший общий делитель): 
Прежде чем двигаться дальше, заполним предложенную пользователем таблицу.
Капитан1312 в его статья (стороны биллиарда будем делить на НОД).

кусочек
На каждый бильярд И
давайте немного займемся координатами
.
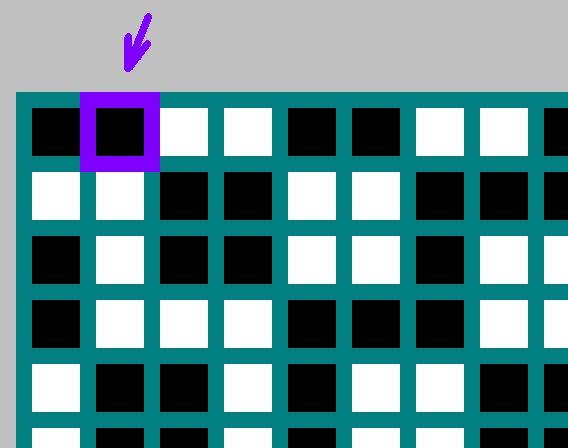
Если
является делителем
- затем бит с координатами
отсутствующий (
).
В данном случае мы берем инвертированный бит с координатами
.
Давайте заполним таблицу.
Начало координат – левый верхний угол.
К
- ширина биллиарда
, К
- высота
.
За каждый бильярд отмечаем немного
, или инвертированный бит
(мы вернемся к этой теме ниже).

Немного о числах Фибоначчи В таблице показаны линии, выходящие из верхнего левого угла.
Если немного построить такую таблицу с координатами
- эти строки видны еще лучше: 
Есть еще один оригинальный способ получить эти строки.
Для каждого
И
, Если
является делителем
, построим последовательность чисел Фибоначчи:
И отмечаем точки на графике
И
: 
Двоичная последовательность
Почему мы инвертировали бит в тех случаях, когда ширина биллиарда? Для относительно простых
И
, траектория мяча проходит через каждую ячейку.
Между верхней и левой стенками бильярда шар каждый раз проходит четное количество клеток.


Биты в левом столбце — это инвертированные биты верхнего ряда.
Нулевой бит не берем — с него начинается траектория: 
Кроме того, мы можем смело выкинуть из этой последовательности каждый второй бит (бит
- инвертированный бит
): 
Получил последовательность
для бильярда
.
Последовательность уникальна для каждого
И
.
Независимо от высоты
мы его не взяли - мяч всегда следует по траектории
между двумя отражениями от верхней стены.
От верхней стены движение всегда начинается с бита «0» (черная ячейка) и заканчивается битом «1» (белая ячейка): 
На самом деле последовательность (которую мы выделили выше –
) показывает, с какой стороны прилетел мяч: 1 — если мяч прилетел, отразившись от правой стены и 0 — если мяч прилетел, отразившись от левой стены.
На картинке траектория полета мяча отмечена черным цветом, если мяч двигался вправо, и белым, если он двигался влево: 
Это интересно С помощью бильярда можно разделить два числа в двоичной системе счисления.
В момент касания верхней или нижней стенки фиксируем направление движения мяча.
Если шарик сдвинулся вправо, пишем 0. Если сдвинулся влево, пишем 1. Фиксируем каждый
касание мяча.
Первый контакт с нижней стенкой.
Мяч двигался вправо.
Записано 0 Второе касание — на верхней стене.
Мяч двигался влево.
Записано 1 Четвертое касание — на верхней стене.
Мяч двигался вправо.
Записано 0 Восьмое касание — по верхней стене.
Мяч двигался вправо.
Записано 0 И т. д. Получили: 0,1001111001111001111. — это двоичное представление дроби.
.

Ээта последовательность(
) содержит всю необходимую информацию о паттерне.
С его помощью мы можем восстановить исходный узор (и даже заглянуть за нижнюю границу узора).
Возьмем квадрат со сторонами
.
Расположим биты нашей последовательности в тех местах, где мяч ударяется о верхнюю стенку (расстояние между соседними касаниями мяча — 2 клетки).
Если соответствующий бит = 1, мы начинаем движение влево, отмечая траекторию через ячейку.
Если бит = 0, мы двигаемся вправо.

При этом не забываем про нулевой бит: 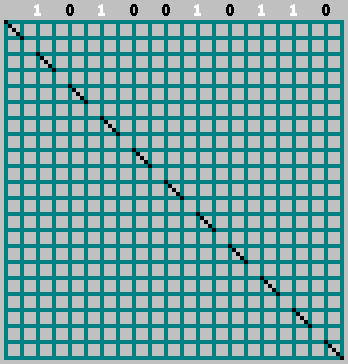
Гифка: 
Получили исходный узор (и посмотрели немного за нижнюю границу): 
Скрипт для визуализации двоичных последовательностей
Мы можем построить эту последовательность, используя остатки от деления.
Одномерный бильярд
На числовой осивозьмем два момента:
И
.

Двигаясь от одной точки к другой, измеряем расстояния
: 
Отметил точку.
Продолжаем измерять расстояние от этой точки, сохраняя направление.
Если вы достигнете точки
или
- изменить направление: 
Как вы можете видеть на изображениях выше, первая точка показывает, где шар касается нижней стенки бильярда.
Этот момент нас не интересует. Мы только исправим моменты
Для
.
Как отметить эти точки? Давайте повернем наш бильярд вокруг своей оси.
.
Давайте отметим точки
.
Теперь, достигнув точки
не меняем направление движения, а продолжаем двигаться к точке
.
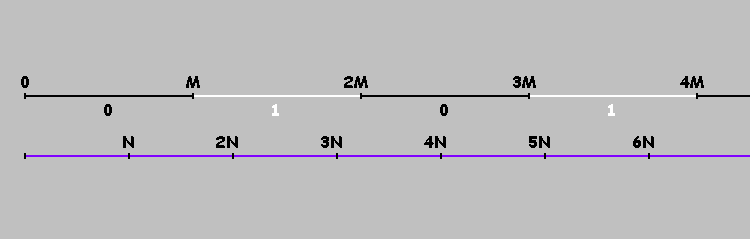
Баллы, кратные
, разделим нашу ось на сегменты.
Условно мы помечаем эти отрезки единицами и нулями (попеременно).
На отрезках, отмеченных нулями, шар (в прямоугольном бильярде) движется слева направо.
На сегментах, отмеченных единицами – справа налево.
Или проще: мяч движется слева направо, если
, Для
(На эту формулу следует обратить особое внимание.
Мы вернемся к ней позже) Легко видеть, что точка, в которой шар коснулся верхней стенки бильярдного стола, является остатком деления.
на
.
В этом случае мы не можем зафиксировать движение мяча в обратном направлении.
Берем всю часть из деления
на
, если оно четное, вычисляем остаток от деления
на
.
Полученный остаток разделите на 2 (расстояние между соседними точками соприкосновения — две клетки).
Мы получили индексы элементов массива, которые нам необходимо заполнить нулями.
Заполняем оставшиеся элементы единицами (шарик переместился с правой стены на левую).
Длина последовательности =
.
Теги: #математика #Алгоритмы #Аномальное программирование #фракталы #хаос #числа Фибоначчи #иррациональные числа #синергетика #математический бильярд #взаимопростые числаfunction sequence(m,n){

-
Анонс Devops-Конференции Devoops 2018
19 Oct, 24 -
У Google Tasks Наконец-То Появился Api
19 Oct, 24 -
Google И Лунное Затмение
19 Oct, 24


