
Наверняка каждый, кто сталкивался с «жемчужным шумом» ( Перлин шум ), попробовал создать текстуру облака.
Потому что оно напрашивается само собой.
Про шум Перлина на хабе я уже писал.
статья , но картинок в нем очень мало.
Вкратце, суть шума Перлина такова: равномерно распределенные случайные точки соединяются плавным градиентом.
Выглядит это не особо привлекательно: 
Однако если вы возьмете только верхнюю половину волн, уменьшите их в 2, 4 и 8 раз и сложите все это, вы получите очень узнаваемые облака: 
+ 
+ 
+ 
= 
Почти то же самое, но 8 раз: 
Закорючка в центре показывает, что такая конструкция является фрактальной и неизбежно имеет фиксированную точку.
На это намекают и соседние закорючки.
На практике это особо не мешает, либо можно засунуть куда подальше.
Вот как формируются облака в текстурном пространстве: 
Возникает резонный вопрос: почему уровни масштабируются ровно в два раза?
Вот пример 8-уровневого облака с разными коэффициентами масштабирования: 
Видно, что до 1.6 облако недостаточно кудрявое, а после 2.6 слишком прыщавое.
Вы можете попробовать заменить магические числа: 
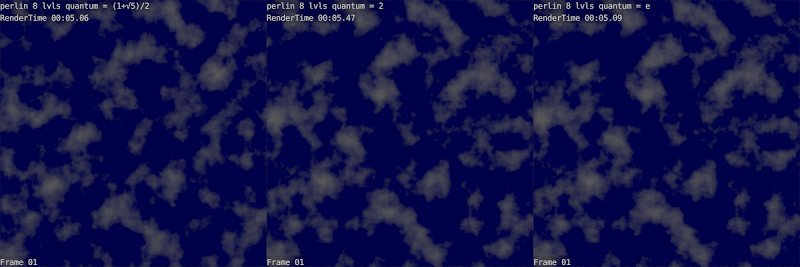
Золотое сечение немного более размазано, число е немного более многолюдно.
Никакого чуда не произошло.
Хотя иногда такое случается и с цифрами.
Два.
Итак, формула холодного облака такова:
Здесь pnt — точка в текстурном пространстве, для которой рассчитывается коэффициент облачности.float acc = 0.0; float amp = 1.0; int i; for(i=0; i<layers; i++){ float v = noise("perlin", scale*pnt); acc += v * amp; amp *= .5; scale *= 2.0; } // max(acc) = (2^n - 1) / 2^n acc *= (float)(1<<(layers)) / (float)((1<<(layers)-1)); return acc * 0.5 + 0.5; }
Например, УФ.
Функция Noise(method, Coords) генерирует значение шума Перлина для заданной точки в диапазоне от -1 до +1. Есть наверняка в любой графической библиотеке, а также в упомянутой выше статье на хабре.
Вооружившись этой формулой, вы можете сгенерировать эту текстуру в 3d и растянуть ее на сферу (не заморачиваясь со сферическими проекциями, а просто подставляя координаты точки сферы в пространстве):
Также можно сгенерировать четырехмерную текстуру и, сместив ее во времени, получить живые облака:
Для большей убедительности координату 3D-текстуры можно также повернуть вдоль экватора на 30 градусов, пропорционально квадрату косинуса широты:
Не знаю, почему 30 градусов и квадрат косинуса, но именно так выглядят настоящие облака на планете.
На самом деле настоящие облака на планете Земля, по данным НАСА ( http://visibleearth.nasa.gov/ ) выглядят так:
И полученная текстура имеет с ними мало общего.
Во-первых, облака должны быть очищены.
Чтобы развернуться, нужно сместить координату текстуры для каждой точки в какую-то сторону, причем так, чтобы для близких точек смещение немного отличалось.
Самый очевидный способ вычислить смещение — снова использовать шум Перлина.
if(Distortion != 0.0) {
point sp = scale[0] * pnt.p;
float st = scale[1] * pnt.t;
pnt.p[0] += Distortion * noise("perlin", sp + vector(1,0,0), st);
pnt.p[1] += Distortion * noise("perlin", sp + vector(0,1,0), st);
pnt.p[2] += Distortion * noise("perlin", sp + vector(0,0,1), st);
pnt.t += Distortion * noise("perlin", sp, st + 1);
}
Здесь float Scale[2] — масштаб в пространстве и времени, pnt — struct { point p; плавать т; } координаты 4d точки.
Если вы попытаетесь сэкономить на вызовах функции шума, то получите в итоге всякие нецензурные выражения, типа такого:
Что вам нужно, так это получить текстуру, которая постоянно искажается в пространстве и времени:
Во-вторых, облака на планете распределены очень неравномерно и вблизи выглядят как чистый перлоновский шум (с масштабами от 8 до 16 от размера планеты).
Лучшее, что я придумал на этой неделе, — это размножить облака.
Большие облака, представляющие собой мегавоздушные потоки, умноженные на маленькие облака, крыльевые облака, приводят к образованию крыльевых облаков, распределенных вдоль мегавоздушных потоков.
∗
=
Это гораздо больше похоже на правду.
Настоящие облака имеют разную степень зернистости, но мне лень этим заморачиваться.
Идея заключалась в том, чтобы сделать еще одно очень большое облако и использовать его значение в качестве параметра масштаба для маленьких.
Этот трюк не сработал — на границах масштаба крылатые облака неприлично сжимаются.
Кроме того, при вращении планеты облака возле экватора замедляются (это даёт поворот на 30 градусов), но я так и не придумал, как это сделать, чтобы текстура не скручивалась в хлам, а плавно испарялась.
Вероятно, вам придется использовать 5d-текстуру и сместить поворот в 5-е измерение, но bledner и язык открытого шейдинга, на котором она была построена, не поддерживают 5d. Какой позор.
Однако на фоне реальной планеты такие облака выглядят вполне прилично:
Хотя их рендеринг занимает в 1,5 раза больше времени.
Анимированное сравнение НАСА и Перлина загружено на YouTube .
Все картинки, включая «непристойность» в высоком разрешении, находятся в пикасоальбом .
Хорошо файл блендера со всеми дизайнами и скриптами на OSL. Теги: #облака #Работа с 3D графикой #3d графика #текстуры

-
Морские Ежи
19 Oct, 24 -
Муонгский Язык
19 Oct, 24 -
Старик Phpclasses.org Обновился
19 Oct, 24 -
Религия В Гаджетах
19 Oct, 24 -
Мета Старается Выглядеть Современно
19 Oct, 24


