На самом деле мы поговорим о двоичная куча и его построение с помощью Sift-Down (или Heapify).
Многие наверняка знают, что построение кучи таким способом осуществляется в 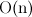
.
Здесь я приведу доказательство этого факта.
Вот пример процедуры построения кучи из массива в Паскале.
Итак, дан массив, состоящий изprocedure siftdown(v:longint); var min,l,r:longint; begin l:=v*2; r:=v*2+1; min:=v; if (l <= s) and (a[l] < a[min]) then min:=l; if (r <= s) and (a[r] < a[min]) then min:=r; if min <> v then begin swap(a[min], a[v]); sift_down(min); end; end; procedure build; var i:longint; begin for i:=n downto 1 do siftdown(i); end;

элементы и

количество звонков оператора
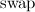
(в процедуре
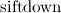
) при построении кучи с использованием этого массива.
Очевидно, 
определяет время выполнения процедуры 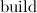
, что нам интересно.
Лемма.
Пусть для некоторого элемента массива при вызове 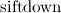
было сделано 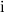
звонки оператора 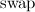
.
Тогда его показатель не превышал 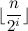
.
Доказательство:
В 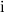
звонки оператора 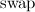
индекс 
элемент увеличивается как минимум 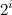
один раз.
Пусть это сейчас 
, т.е.

.
Затем после 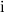
у нас есть проблемы 
, что невозможно, так как в нашей куче 
элементы.

Оценим теперь сверху величину 
.
Пусть элемент массива имеет индекс 
.
Будет 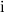
, такой, что 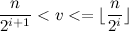
.
Тогда для того, чтобы элемент массива с индексом 
встал на место в куче, больше не потребуется 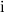
звонки 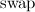
(по лемме).
Количество элементов с такими индексами есть величина 
, который в 
уходит в ноль.
Таким образом, 
В 
члены равны нулю (поэтому цикл в процедуре 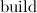
ты можешь начать с 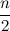
).
Оценим левый множитель в каждом слагаемом суммы как 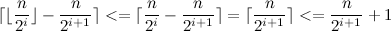
Отсюда мы имеем: 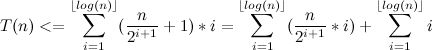
Давайте оценим каждую из сумм.
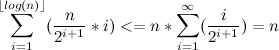
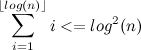
Таким образом, 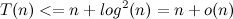
.

ограничено сверху функцией, которая 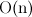
.
Означает, 
.
Таким образом, время выполнения процедуры 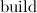
существует количество, пропорциональное 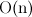
.
Теги: #оценка алгоритмов #математика #двоичная куча #куча #построение кучи #Алгоритмы #математика
-
Подсчет Количества Раздач Логотипа И Знака
19 Oct, 24 -
Линейка Дистрибутивов Windows 7
19 Oct, 24 -
Google, Android И Открытый Исходный Код
19 Oct, 24


