Дискретное Преобразование Фурье Фрактального Броуновского Движения

Фрактальное броуновское движение (FBD) относится к классу рассматриваемых функций, определенных на конечном интервале и равных нулю вне его, к которым относятся кусочно-непрерывные функции, удовлетворяющие условию роста:

, где находится функция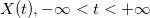

, удовлетворяет условию:

преобразование Фурье Для FBD мы интерпретируем процесс

как временной процесс.

Существует частотная область, в которой функция представляет собой сумму составляющих, имеющих определенную частоту.

Функция

можно разложить как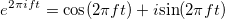

.

Компонент

с частотой

имеет форму: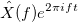

, Где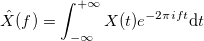

.

Функция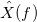

называется преобразование Фурье .

Спектральная плотность Полная энергия начального процесса равна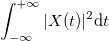

.

По теореме Планшереля:

.

Средняя мощность функции

на сегменте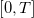

определяется как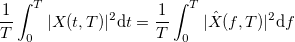

.

Тогда спектральная плотность мощности равна: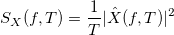

Если длина отрезка стремится к бесконечности, то: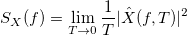

.

Поскольку функция

описывает FBD с Параметр Херста , Что:

Дискретное преобразование Фурье FBD Процесс моделирования FBD можно упростить, аппроксимировав преобразование Фурье рядами Фурье с учетом сохранения свойств спектральной плотности.

После этого с помощью обратного преобразования Фурье получаем ФБД.

Если

тогда функция

реальная стоимость Поэтому приведенный ниже алгоритм использует это условие сопряженной симметрии.

Алгоритм построения кривой FBD:

— нормально распределенная случайная величина с нулевым математическим ожиданием и единичным стандартным отклонением.

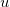
— равномерно распределенная случайная величина на единичном интервале.

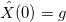
Для

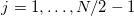
Значения преобразования Фурье

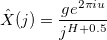
Для

—

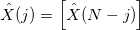
Для каждого

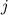
мы рассчитываем: амплитуда (абсолютное значение комплексного числа

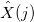
), фаза (значение аргумента комплексного числа

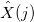
, т.е.
угол, выраженный в радианах) Рассчитаем значения FBD: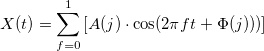

На рисунке показаны некоторые варианты FBD для различных показателей Херста.
Пример использования генерации FBD Дана начальная серия валютной пары доллар-рубль за период: 05.05.2005 – 01.05.2015. Давайте рассчитаем доходность обменного курса, используя RS-анализ Найдем показатель Херста для пары доллар-рубль: Н=0,64 далеко от среднего значения Е(Н)=0,52 на 5,64 стандартных отклонения.
Величина ЧАС - значительный.
Серия стойкая, потому что Н> 0,5 , нормированный диапазон меняет масштаб во времени быстрее, чем квадратный корень, процесс имеет долговременную память (подробнее в [1]).
Отсутствие цикла позволяет с помощью параметра Херста моделировать фрактальный шум с помощью фильтрации Фурье.
Построим в частотной области преобразование Фурье фрактального броуновского движения со случайными амплитудами и фазами, удовлетворяющими свойству спектральной плотности.
С помощью обратного преобразования Фурье получаем искомый фрактальный шум.
Затем мы генерируем 10 000 возможных вариантов FBD с показателем Херста 0,64. Таким образом, мы получаем распределение прогнозных значений курса валют.

На рисунке представлен график исходного ряда значений курса доллара к рублю, а также 90% децильное распределение и математическое ожидание прогноза: с вероятностью 90% можно утверждать, что курс не превысит значений верхней кривой среднее значение курса имеет тенденцию к снижению, в середине мая в среднем цена за доллар составит 52,3 рубля, начало июня - 51,6, начало июля - цена падение до 48,7 руб.

Библиография: Гончаренко А.

В.

Фрактальный анализ динамики валютной пары доллар/рубль // Управление рисками в кредитной организации.

№ 2(18).

2015. С.

18-22. Теги: #фрактал #временные ряды #Алгоритмы #Хёрста #измерение #Брауновское движение #преобразование Фурье #валюта #прогнозирование #Алгоритмы #математика