Часть 1. Собственно, до нас уже все поделили! Часть 2. Истина где-то там В Последняя часть мы расширили алгебру и смогли арифметически делить на ноль.
В качестве бонуса этот метод оказался не единственным.
Однако все эти алгебры не ответили на вопрос: «Что внутри или почему нам это не показываютЭ» В то время как древние вязаные узлы , вопрос не могло возникнуть .
Теперь, куда бы вы ни посмотрели, «бла-бла, за ≠0».
Так что ответ спрятан где-то между узлами и настоящим.
В математике все строго и последовательно, а значит, ответ не мог потеряться.

Мы постараемся максимально приблизиться к ответу.
Эта часть почти целиком посвящена философии арифметики.
Скорее всего, часть материала окажется для вас тривиальной.
Однако мы здесь не повторяем школьный курс арифметики.
Материал структурирован так, чтобы подчеркнуть структуру арифметики.
Надкусываем его с разных сторон и отрываем пласты.
Цель – понять, что где находится.
2. Истина где-то рядом
2.1 Зачем вообще беспокоиться?
Чтобы снова броситься в дебри, хотелось бы понять, почему периодически возникает этот вопрос и почему стоит искать ответ. Давайте вспомним школьные годы, время, когда нам впервые сказали: «На ноль делить нельзя», так категорично.«Ты не можешь этого сделать!» А ведь до этого в математике все было логично и последовательно.
Арбузы добавляли и дыни вычитали, яблоки закатывали.
Откуда ни возьмись, в самом начале изучения математики появился первый запретный плод. Классический набор ответов только расстраивает
- «Ты не можешь этого сделать!» или «Проверь на калькуляторе» — без комментариев.
Специальная педагогическая методика.
- «Яблоко можно разделить на две части.
Ты и твой друг Коля.
Возможно на троих.
А если человека разделить на ноль, то сколько раз его нужно отрезатьЭ» - да, непонятно.
И неприлично отвечать вопросом на вопрос.
Для чего нужен учитель? Говорят, математика «красивая», математика «королева», а тут такой конфуз.
- «2∙0=0 и 3∙0=0, разделим оба равенства на ноль, тогда получится, что 2=0/0 и 3=0/0. Так 2=3 или чтоЭ» - пример, конечно, понятен.
Но подобные примеры не только не отвечают на вопрос, но и сеют страх перед наукой.
А что, если есть что-то еще, что нельзя разделить или умножить? Что, если я поскользнусь? А может, учитель сам не догадался?
- «Чтобы понять, нужно много знаний.
Этому учат в университете, и не все» — ну да, а что нельзя разделить? До этого момента наши причинно-следственные связи не были нарушены, они шли от простого к сложному.
Но ноль — это число как число.
Дивизия – это операция как операция.
Запрет неожиданный!
Нет другого выбора, кроме как двигаться дальше и приобретать новые знания.
В голове происходит «скачок знаний», как будто было упущено тысячелетие эволюции математики.
И это только начало.

" .В старших классах откуда ни возьмись появляются формулы окружностей и треугольников, дискриминанты, тригонометрические тождества и т. д. Что они имеют общего? Все они пришли сверху, совершенно неизвестно откуда.не нужно проявлять лишней спешки, нужно дать ученику время привыкнуть к внутреннему перевороту, происходящему в нем в результате акта познания », — Ф.
Кляйн, «? элементарная математика с высшей точки зрения»
Их просто нужно использовать или, в худшем случае, запомнить.
Поступив в университет, большинство, вместо того, чтобы вернуться к пропущенному материалу, учатся на уровне высшего образования с упором на свою специальность.
Объем формул, пришедших сверху, уже совершенно не сбивает с толку.
Да, систему образования можно понять.
Специалисту платят за результат, а не за то, что он знает, откуда в его расчетах берется показатель степени.
В результате мы не приходим к выводам, как это делают математики.
В момент «скачка познания», то есть когда мы отбрасываем часть логических цепочек, совершается таинство.
Мы принимаем на веру то, что нам говорят. Учебник превращается в священное писание! 
Запрет на деление на ноль — первый и самый навязчивый запрет математики.
Поэтому оно запоминается на всю жизнь.
Это еще и педагогическая проблема, которая накладывает отпечаток на всю математику как «тайна, окутанная мраком».
Это сложная задача, поэтому путем сравнения легко найти большинство недостающих логических цепочек.
Священное Писание можно снова превратить в учебник.
Причина запрета должна быть строго определена.
Задача учителя – ясно это представить.
Наука не должна сеять сомнения.
2.2 Что такое разделение?
Капитан Очевидность утверждает, что для того, чтобы разделить на ноль, нужно знать, что такое деление и что такое ноль.К сожалению, Google предполагает, что многие приверженцы «магии деления на ноль» не проходят даже первого круга этого ада.
А именно понять, что они собираются делать и с чем.
Давайте заглянем в Википедию:
Дивизия (операция дивизии) — одно из четырёх простейших арифметических действий, обратное умножению.Что из этого следует:Деление — это операция, подсчитывающая, сколько раз одна вещь содержится в другой.
- Разделение не самостоятельная операция.
Это определяется через умножение .
Если вы посмотрите на определение умножения, оно определяется через сложение.
Вычитание также определяется путем сложения.
Дополнение независимое и ни от кого не зависит.
- В определении нет упоминания нуля.
Учитывая широко распространенный запрет на деление на ноль, это очень странно.
Кстати, в определениях других арифметических операций нуль не упоминается.
- Вторая часть определения не является частью определения, это всего лишь объяснение.
В этом можно убедиться, сравнив с аналогами в другие проверенные источники .

Похоже, самое полезное, что мы здесь нашли, — это связь между операциями.
Можно сказать, что деление — это вино третьего нажима, умножение и вычитание — второго, а сложение — первого.
Возможно, именно по этой причине деление стало сбоить при работе с нулем.
2.3 Генеративные операции
Так что только операция добавление содержит правило, как определить результат операции (сумму) по двум исходным аргументам (сложениям).Все остальные арифметические операции используют это правило (сопоставления чисел), но дополнительно накладывают свои собственные "дополнительные условия" .

В зависимости от «дополнительных условий» арифметические операции можно разделить на прямой И обеспечить регресс :
- Прямые операции — сложение, умножение и возведение в степень.
Выражая эти операции через сложение, все члены остаются известными.
Определить результат любой из операций не составляет труда.
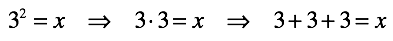
- Обратные операции: вычитание, деление, извлечение корня (логарифм).
Эти операции берут за основу соответствующую прямую операцию и «инвертируют» ее.
Таким образом, выражая операцию через сложение, хотя бы одно из слагаемых оказывается неизвестным.
Этот срок является результатом операции.
Сумма обычно известна.
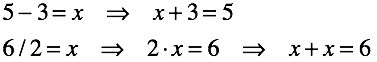
Определение результата операции, в общем-то, нетривиальная задача.
Они есть закрыто .
То есть тип результата полностью определяется типами входных чисел (получить дробный результат из произведения двух целых чисел невозможно).
Обратные операции закрыты лишь частично (значение корня целого числа может быть целым числом, а может и не быть).
В тех случаях, когда найти результат не удается, операция оказывается не определено .
Эта проблема давно решена простым способом: полученные обозначения операции и числа рассматриваются как новый тип чисел: ![]()
.
Таким образом, можно сказать, что обратные операции «рождают» новые типы чисел.
На математическом языке:
Вообще недопустимо использование термина «обратная операция» для обозначения способности операции генерировать новые типы чисел.Разделение является одной из генерирующих операций.Например, «дополнительными условиями» могут быть:
- поместите результат операции в один или несколько термов (как показано в примере выше);
- определить результат операции как ответ на вопрос, сколько слагаемых было задействовано в операции (дробные числа, иррациональные числа с использованием корня);
- определить результат операции как сумму бесконечного числа слагаемых.
В этом случае известны все члены (число Пи и число Эйлера).
Возможно, что-то пошло не так в процессе родов и новорожденный получил травму.
Для того чтобы ответить на этот вопрос, нужно понять, откуда взялось деление и откуда взялся ноль.
2.4 Эволюция арифметики
Давайте попробуем структурировать наше понимание арифметических операций и типов чисел, которые они генерируют. Для наглядности представим один из вариантов того, как может протекать эволюция арифметики.
2.4.1 Область применения
Мы в пещере.Никто не родился со способностью считать.
Однако в процессе «созерцания» появилось понимание того, что понятие «количество» .
То есть мы знаем, что у двух мамонтов и двух яблок есть что-то общее и мы можем выразить это, согнув пальцы.
Соответственно, ничего, кроме натуральных чисел, мы на данном этапе не знаем.
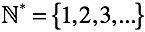
Набор натуральных чисел отмечен звездочкой «*».
Здесь и далее подчеркивается отсутствие понятия «ноль».
Есть несколько формальных определений последовательности натуральных чисел.
Мы возьмем за основу Аксиомы Пеано .
Примечательно, что эти определения не были описаны древними.
Они появились только в XIX веке, а затем прошли процедуру уточнения (в первоначальном варианте их было девять, в современном виде уже пять).
Рассмотрим формальные определения и их сущность в рамках нашей задачи (традиционное словесное описание можно найти в Википедии ):
-
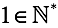
Число «один» есть и оно естественно. -

Представлено следовать функции S(х).Для всех натуральных аргументов возвращается следующее натуральное число.
В первом приближении (очень грубом) это S(x)=x+1, например 2=S(1) и 3=S(S(1)).
-

Вводится явный запрет на глобальную цикличность генерируемой последовательности чисел.При генерации чисел мы не можем получить тот элемент, с которого начали генерацию, то есть единицу.
-
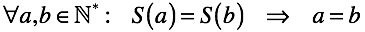
Различные аргументы функции Follow должны давать разные результаты.Таким образом, вводится явный запрет на локальное зацикливание.
То есть функция Follow не должна повторно генерировать число, которое уже было сгенерировано.
-
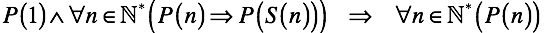
Математическая индукция , позволяющий подняться с уровня элементов последовательности на уровень последовательности в целом.Если есть заявление «Р» верно для одного и для каждой пары соседних элементов, тогда оно верно для всех элементов последовательности.
Например.
Для чисел 2 и 3 верно, что между ними есть один средний элемент 2,5, для 3 и 4 — 3,5 и т. д. Делаем вывод, что между любыми соседними натуральными числами есть средний элемент и он единственный.
Запрет цикла всегда требует наличия следующего элемента.
Вот так математически понятие «бесконечность» основано на понятии «количество».
Понятие «бесконечность» не может существовать без понятия «количество».
На математическом языке:
Довольно часто в аксиомах Фортепиано в качестве «исходного элемента» принимают ноль.Почему этого сделать нельзя, выяснится при описании операции «вычитания» (очень скоро).
Следуйте функции не использует операцию сложения в прямом смысле этого слова.
Это фундаментальная функция, которая используется как для построения набора натуральных чисел, так и для формальное определение операции сложения .
То есть и числа, и арифметические операции определяются с помощью функции Follow. Функция отслеживания включена класс примитивно-рекурсивных функций обсуждалось в теория алгоритмов .
Как известно, концепция рекурсия не содержит требования своей конечности (достижимости терминальные ветки ), а значит, также неявно определяет понятие «бесконечность».
2.4.2 Дополнение
Первая операция, возникшая в ходе нашей эволюции.Как бы вы не сгибали пальцы, результат будет неизменным.
Пока не лидер сумма пальцев может быть немного больше, чем у всех остальных.
Если пальцев не хватает, всегда можно вызвать научного сотрудника в пещеру и расширить битовую сетку.
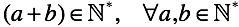
2.4.2 Вычитание
В четверг охотники застрелили 12 мамонтов.Мы съели 5 штук в пятницу.
Сколько мамонтов осталось? 
Проблему хорошо решает введение разгибания пальцев.
Но такой подход не всегда работает. Например, для оценки запасов на выходные охотник загибает семь пальцев на остаток, вытягивает пять пальцев на субботу (норма потребления за день) и «пытается» разжать на воскресенье.

В этот момент между «try» и «catch» возникает ArithmeticException. Результат оказывается не определен .
Наша операция определена только для случая, когда уменьшаемое больше вычитаемого.
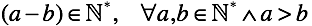
Однако определение вычитания не накладывает никаких ограничений.
Чтобы избавиться от требования «a > b», введем «правило перестановки» .
То есть поменяем местами уменьшаемое и вычитаемое.
Но чтобы тождество оставалось верным, результат должен быть отмечен каким-либо маркером, например, знаком минус.
Обычны всевозможные маркеры по математике (например, признак отсутствия нуля в ![]()
).
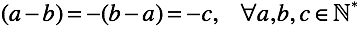
Благодаря вспомогательной операции «перестановки» мы пришли к первой абстракции — « отрицательные числа «Отметка в виде знака «минус» на натуральном числе есть не что иное, как знак отложенного вычитания (но это только пока).
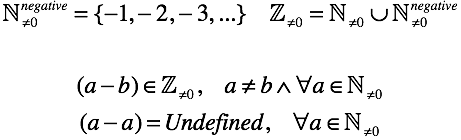
У нас остался только один неопределенный случай, когда уменьшаемое и вычитаемое равны.
Если мы хотим его определить, то нам придется ответить на вопрос, что такое понятие «ничего» .
Хотя зачем все эти сложности, давайте обозначим «ничего» символом «0» (позже мы углубимся в это полностью).

Осталось зафиксировать наше решение в виде «правила прибавления/вычитания нуля» .
Они следуют из определения нуля после пары простых перестановок: 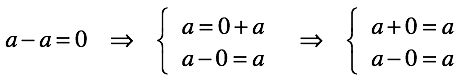
Посмотрим, насколько хорошо работают введенные правила.
Решая уравнения, мы всегда можем найти неизвестную треть, используя два известных числа.
Неважно, в какой части уравнения оно находится, решение всегда очевидно.
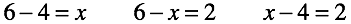
Отрицательные числа появились в результате перестановки, а ноль заполнил «ничто».
Отрицательные числа и ноль создаются разными способами.
Далее мы рассмотрим две ветви эволюции: отдельно все числа без нуля и отдельно ноль.
2.4.3 Умножение
Умножение по определению является сокращением сложения.При умножении натуральных чисел результат может быть только натуральным.
На этом этапе эволюции полезность определения для нас заканчивается.
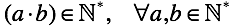
Для отрицательных чисел в определении не сказано ни слова о том, как их умножать.
Эти правила формировались постепенно.
при решении прикладных задач .
В современной интерпретации они известны как дополнение к умножению в виде «правила знаков» .
Они определены настолько хорошо, что при применении к ненулевым целым числам операция остается закрытой.
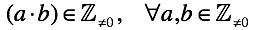
В случае нуля ситуация кардинально иная.
Вводится еще одно правило – «правило умножения нуля» (умножение любого числа на ноль дает ноль).
Но это правило только кажется новым.
Никакого другого правила мы ввести не можем.
Определение умножения тесно связывает нас со сложением.
Расширяя умножение посредством сложения, мы используем «правила сложения/вычитания нулей»; соответственно, мы не можем получить ничего, кроме нуля.
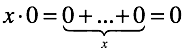
На математическом языке:
Если вы сравните операции сложения и умножения в арифметике и общей алгебре, вы заметите одно серьезное различие.В арифметике эти операции связаны по определению.
Распределительный закон является следствием этих определений.
В общей алгебре, наоборот, операции описываются независимо друг от друга, и уже в определении поля (точнее кольца) они связаны дистрибутивным законом.
Следовательно:
Поле, венец универсальности, притянуто «за уши» к элементарной арифметике.
- В определении поля есть требование обратного элемента.
Более того, для умножения и сложения требование описывается несимметрично.
Отсутствие обратного элемента для умножения допускается для нейтральных элементов для сложения, но не наоборот.
- Для придания симметрии при описании колеса Пришлось отказаться от обычного закона распределения, а значит и от работы поля.
Но чтобы избавиться от этой поддержки (чтобы описать требования к операциям симметрично), нам придется расширить определение распределительного закона (начиная, конечно, с кольца).
Есть основания полагать, что венцом универсальности может стать еще одна алгебраическая система, для которой поле окажется частным случаем.
2.4.4 Дивизион
Деление – это операция, обратная умножению.В уравнениях с положительными и отрицательными числами появляется возможность подставлять некратные числа.
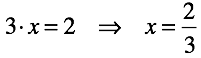
В результате операция генерирует "рациональное число" .
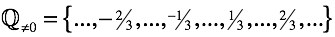
Для их укладывания в арифметику в комплект входят «Правила обращения с обыкновенными дробями» .
К счастью, эти правила гармонично сосуществуют с введенными нами ранее «правилами знаков».
В результате уравнения сохраняют способность определять неизвестное по двум известным числам в любом расположении.
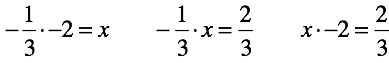
В случае нуля его можно умножить на рациональные числа.
Всё, гармония закончилась! Лишь для двух из трех типов уравнений с произвольными числами можно найти решение.
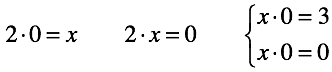

Во-первых, стало возможным составить уравнение с настолько неудобными числами, что мы не смогли бы найти ни одного решения.
Решение «невозможно».
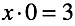
Во-вторых, стало возможным создать уравнение, у которого имеется бесконечное число решений.
Также невозможно выбрать только один из них.
Решение «непонятное».

Нетрудно догадаться, что корень проблемы деления на ноль лежит в «невозможности» и «неоднозначности» умножения нуля.
Умножение, в свою очередь, передает «правила сложения/вычитания нуля».
Фактически, можно определить уравнения, обладающие одинаковыми свойствами, используя только сложение.
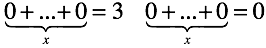
В обоих уравнениях нужно определить количество нулей, которые нужно добавить, чтобы получить произвольное число или ноль.
Ничего качественно нового дивизия не принесла.
Произошла трансформация «невозможности» и «неясности» сложения в конкретные сущности.
, в неопределенностях вида 1/0 и 0/0 соответственно.

Оказывается, деление, как первый подозреваемый, не виновато в том, что на ноль делить нельзя.

Пока не существует понятия «ноль», все операции, включая возведение в степень и извлечение корня (логарифмов), хорошо замкнуты (справедливо для комплексных чисел) и арифметика работает прекрасно.
Но есть одно «но»: при такой конфигурации арифметики операция вычитания оказывается не до конца определенной.
После ввода нуля сложение и вычитание работает хорошо.
Для остальных операций это скорее повод для установки костылей( ![]()
), а не равное число.
2.5 Что такое ноль?
Итак, поскольку операция деления оказалась не виновата в запрете деления на ноль.Давайте тогда попробуем собрать воедино все, что мы знаем о нуле:
- Необходимость в нуле появилась при определении операции вычитания.
- Чтобы устранить большую часть неопределенностей вычитания, было введено «правило перестановки».
Знак минус перед числом по сути является маркером «отложенного вычитания».
Все, с чем не справлялось «правило перестановки», покрывалось нулем.
Фактически, ноль был введен для обозначения понятия «ничего».
.
В предыдущей части статьи (с проективным расширением числовой прямой) мы «на ровном месте» ввели беззнаковую бесконечность.
Ноль, аналогичная «заглушка» для всего, чего мы не понимаем.
Последствия в виде возникновения новых неопределенностей оказываются весьма предсказуемыми.
- Понятие «ничто» не имеет никакой связи с понятием «количество».
(основы для определения натуральных чисел и сложения).
Эти понятия существуют сами по себе и мы можем «созерцать» их совершенно независимо, например, «пять яблок» и «вакуум».
Отсюда следует, что по своей сути ноль также не является

-
Планета Эксо
19 Oct, 24 -
Какой Облачный Сервис Вы Используете?
19 Oct, 24 -
Codraw — Стартап За Неделю
19 Oct, 24 -
Необычные Http-Заголовки
19 Oct, 24


