Анализ Эффектов Обучения С Использованием Python И Линейной Регрессии

Был ли эффект от регулярных тренировок? Я проанализировал данные своих предыдущих тренировок, используя несколько распространенных методов, и получил неоднозначные результаты.

Это продолжение серии статей об анализе данных персональных тренировок из набора FIT-файлов, которые создаются при использовании носимых устройств, включая фитнес-браслеты, часы, смартфоны и т. д. В предыдущих трех статьях я говорил о как получить доступ к данным завершенных тренировок , как визуализировать показатели на графике И как проводить их пространственный анализ .

В этой же статье я затрону тему анализа эффективности тренировок и расскажу, какие математические модели существуют для оценки их прогресса.

Для решения задач я использовал несколько библиотек Python, предназначенных для работы с данными и построения моделей линейной регрессии — Панды, Numpy, Matplotlib, Scipy, Statsmodel .

Какие тренировки я исследовал?

1. Наличие более сотни записей данного вида тренировок, выполненных за последние два года на одном и том же типе тренажера с использованием одних и тех же датчиков (измерителя мощности, датчика частоты вращения педалей и пульсометра) и одного и того же приложения;
2. Тренировки проводились в зимний период в закрытых помещениях при относительно одинаковых условиях, то есть исключается фактор разных погодных условий (температура воздуха, сила ветра, влажность);
3. Обучение проводилось регулярно примерно в одно и то же время суток и дни недели;
4. Относительная сопоставимость условий обучения позволяет сравнивать имеющиеся данные;
5. И последнее, это непосредственный интерес к тому, есть ли прогресс в плане тренировок.

Ключевые показатели обучения включают в себя:

• Мощность (мощность, Вт) – усилие, приложенное к педалям, умноженное на скорость.

  Измеряемый в ваттах, он показывает эффективность работы, которую вы выполняете при вращении педалей;

• Каденция (каденс, об/мин) – частота вращения педалей или, другими словами, количество оборотов педалей велосипедиста, совершаемых за одну минуту;
• Частота сердечных сокращений (уд/мин) – частота сердечных сокращений (ЧСС) или другими словами количество ударов сердца в минуту.

Если рассматривать файл FIT, то упомянутые данные для каждой тренировки сохраняются в сообщении Записывать , обобщенные данные – в Сессия .

Стоит отметить, что уровень точности датчиков и их стабильность пока не претендует на абсолютную значимость результатов анализа, а сам анализ интересен лишь с любительской точки зрения.

Анализ результатов тестирования FTP

Тестирование FTP при регулярных тренировках проводится примерно раз в четыре недели.

Стандартный протокол включает в себя несколько интервалов:

• Разминка с переменной частотой вращения педалей;
• 5 минут максимальных усилий;
• Восстановление/отдых;
• 20 минут максимальных усилий (ключевой интервал);
• Хитч.

Сравнение результатов тестирования FTP

Профиль тренировок для теста FTP на 28 января 2021 года включает 1 – разминка, 2 – 5 минут максимальных усилий, 3 – отдых, 4 – 20 минут максимальных усилий, 5 – заминка (всего 45 минут).

.

Как построить подобный график с помощью matplotlib я описал в этой статье, код доступен Здесь .

Расчет FTP довольно прост и состоит из выбора ряда значений мощности (интервал 20 минут) и нахождения среднего значения.

Полученное среднее значение умножается на 0,95. Серийный номер второго из таблицы Записывать может быть создан с помощью функции SQL КЛАССИФИЦИРОВАТЬ :

   

 # importing libraries
 import psycopg2
 import pandas as pd
 
 activity_id = 80286974365
 
 # connecting to a training record data
 conn = psycopg2.connect(host="localhost", database="garmin_data", user="postgres", password="******")
 df = pd.read_sql_query("""select timestamp, heart_rate, cadence, power, 
 rank() over (order by timestamp asc) as rank_no 
 from record 
 where activity_id ={} order by timestamp asc""".

format(activity_id), conn)
 
 # ftp calculation
 start = 20*60
 end = 40*60
 df = df.loc[((df['rank_no'] > start) & (df['rank_no'] < end))]
 ftp = df['power'].

mean()*0.95
 

   

Всего за сезон было проведено три FTP-тестирования.

Сравнивая их результаты с течением времени, можно сделать вывод, что прогресс в обретении спортивной формы есть.

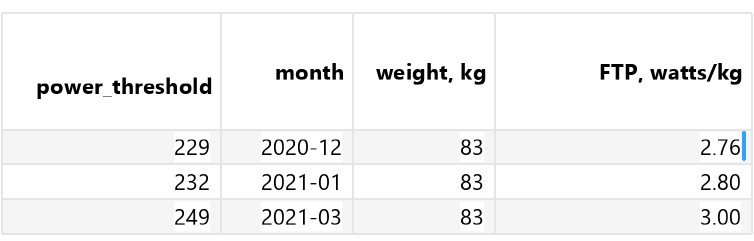
Использование значения FTP широко распространено среди велосипедистов-гонщиков, поскольку оно сопоставимо между спортсменами.

Оценить свой уровень можно с помощью Стол Нди Коггана .

Использование техники PWC170

Выбор этой величины обусловлен тем, что адекватное функционирование кардиореспираторной системы с физиологической точки зрения ограничивается диапазоном частоты сердечных сокращений от 100 до 170 ударов в минуту, а также тем, что связь между частотой сердечных сокращений и силой сердечных сокращений ограничена.

Выполняемая физическая активность у большинства здоровых людей линейна вплоть до частоты сердечных сокращений, равна 170 ударам в минуту .

Тест состоит из следующих интервалов:

• 5 минут первой нагрузки W1 (нагрузка устанавливается исходя из веса человека).

  На последних минутах фиксируется значение ЧСС f1;

• 3 минуты отдыха;
• 5 минут второй нагрузки W2 (нагрузка устанавливается исходя из мощности первой нагрузки и значения ЧСС, при котором эта нагрузка была завершена).

  На последних минутах фиксируется значение ЧСС f2.

Расчет PWC170

Основанный на таблицы с вариантами первой загрузки , я определил значение 130 Вт и сделал следующий запрос к таблице Record:

select to_char(timestamp, 'YYYY-MM') as month, heart_rate from record where activity_id in (select activity_id from session where sub_sport = 'virtual_activity' and timestamp::text between '2020-10-31' and '2021-04-01') and power between 125 and 135 and heart_rate > 80 and cadence between 80 and 90

Подзапрос выбирает только велоспорт в помещении (sub_sport='virtual_activity') на сезон 2020-2021, устанавливается ограничение на значения мощности от 125 до 135 (так как на машине обычно сложно поддерживать определенное значение), heart_rate > 90, чтобы исключить пропущенные и неправильные значения, средний темп от 80 до 90. Далее строим график распределения значений пульса при нагрузке 130 Вт за первый и последний месяц тренировок:

import matplotlib.pyplot as plt from matplotlib.pyplot import figure fig, (ax1, ax2) = plt.subplots(1,2) fig.suptitle('First and Last Months Heart Rate values distribution at 130 watts') N1, bins1, patches1 = ax1.hist(w1_df11.heart_rate, bins=np.arange(110,190,1)) for i in range(19,20): patches1[i].

set_facecolor('r') ax1.set_ylim(0, 35) ax1.set_xlabel("HR, bpm") ax1.set_ylabel("Counts") N2, bins2, patches2 = ax2.hist(w1_df03.heart_rate, bins=np.arange(110,190,1)) for i in range(16,17): patches2[i].

set_facecolor('r') ax2.set_ylim(0, 300) ax2.set_xlabel("HR, bpm") ax2.set_ylabel("Counts") plt.rcParams['figure.figsize'] = [16, 4] plt.show()





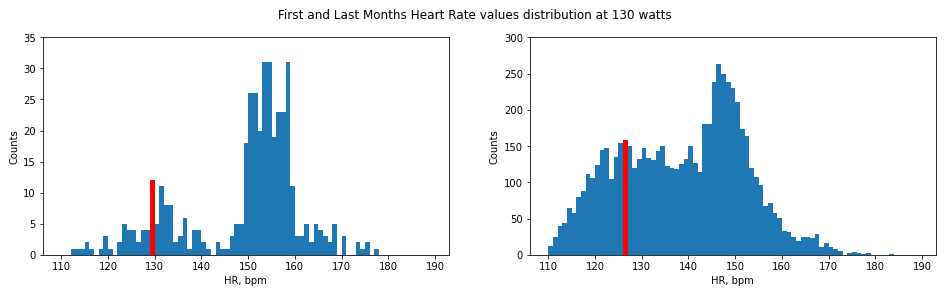
График напоминает бимодальное распределение с двумя пиками.

Первый пик (основанный на значениях сердечного ритма), скорее всего, относится к восстановительным тренировкам и разминкам, а второй пик относится к интенсивным интервалам тренировок.

Первый пик больше коррелирует с тестом PWC170, поэтому в качестве ЧСС первой нагрузки f1 я выбрал наиболее распространенное значение из первого пика.

Таким образом, мы получаем значение f1 = 130 уд/мин для первого месяца и f1 = 127 уд/мин для последнего месяца тренировок.

По таблице определить величину второй нагрузки интервал от 120 до 129 уд/мин соответствует значению 180 Вт. Аналогично построим распределение значений пульса при нагрузке 180 Вт, изменив интервал в запросе на мощность между 175 и 185 .

График напоминает отрицательно перекошенное нормальное распределение (перекошенное влево) с одним пиком — выберем его значение в качестве ЧСС второй нагрузки.

Применение метода графической интерполяции

format(np.round(W3, 2)), size=10, color='r') ax2.set_xlim([120, 200]) ax2.set_ylim([120, 180]) ax2.set_xlabel("Power, watts") ax2.set_ylabel("HR, bpm") plt.rcParams['figure.figsize'] = [10, 5] plt.show()









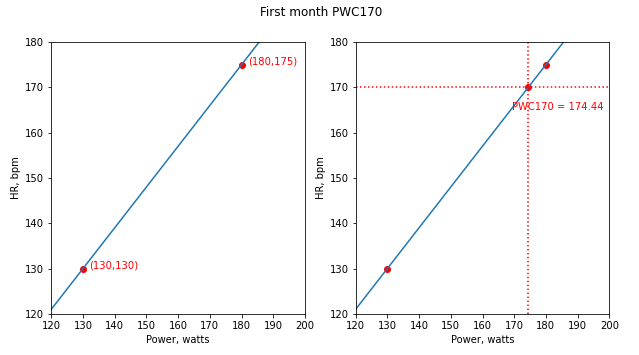
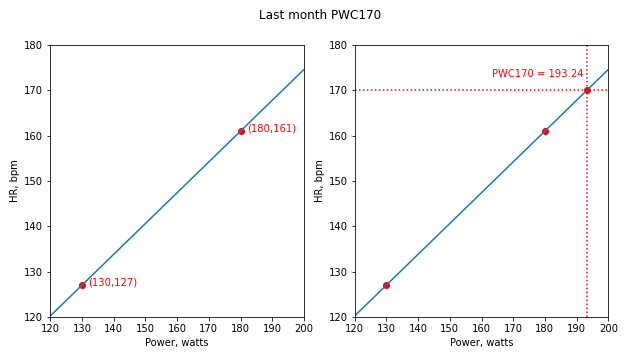
При сравнении двух полученных значений PWC170 за первый и последний месяцы — 174,44 и 193,24 Вт, можно сделать вывод, что прогресс есть.

Однако тест нельзя назвать выполненным по стандартному протоколу.

Точность используемой методологии можно подтвердить только путем анализа гораздо большего количества данных от разных людей.

В будущих сезонах я постараюсь провести тест максимально приближенно к оригинальному методу, чтобы получить более значимые результаты.

Применение метода линейной регрессии

В нескольких найденных статьях в открытом доступе также используется это предположение и применить модель линейной регрессии рассчитать градиент, который должен отражать текущее физическое состояние спортсмена.

В другой статье Предложен вариант расчета значений ЧСС через величину мощности по следующей формуле:



Также приведен пример из приложения с открытым исходным кодом.

Золотой гепард , где есть функция построения графика зависимости пульса от мощности.

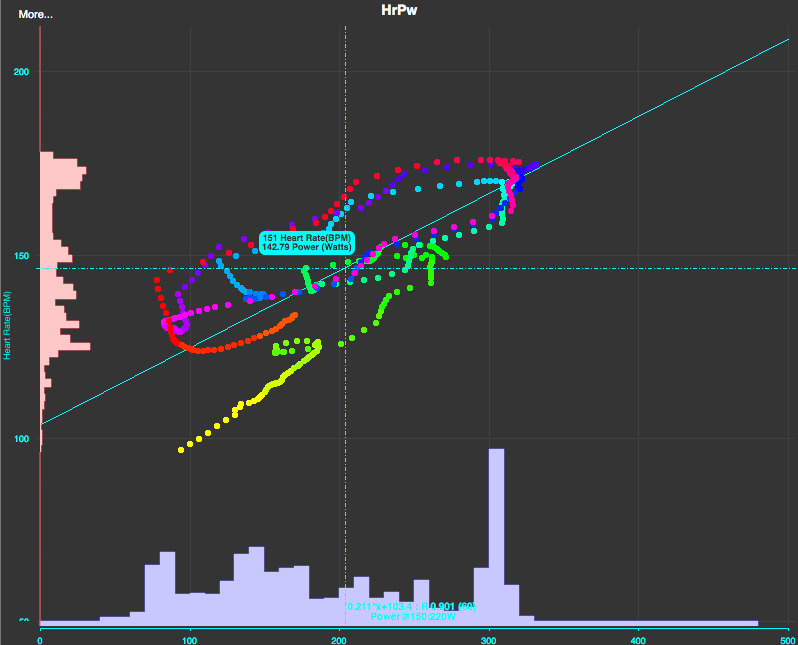
Какие данные я использовал для анализа?

Если значение k уменьшается, то при большем увеличении мощности значение ЧСС увеличится на меньшую величину.

Для анализа я решил использовать интервал разминки для каждой тренировки, во время которого поддерживались примерно сопоставимые условия:

• Равномерное увеличение мощности при стабильном темпе вращения педалей;
• Частота сердечных сокращений всегда будет ниже порогового значения, и влияние предыдущих интервалов не будет, поскольку это всегда первый интервал тренировки.

На рисунке ниже представлены графики двух тренировок: для первой можно выделить 7-минутный разминочный интервал со стабильным ритмом и равномерным увеличением мощности (от 2 до 9 минут), для второй - нет. возможно из-за наличия кратковременного повышения мощности на 5-6 минут.

Построение модели линейной регрессии

Записывать .

Каждая запись в таблице Записывать соответствует 1 секунде тренировки.

Ниже приведен пример кода для загрузки данных с 1 по 10 минуты тренировки:

import pandas as pd import psycopg2 activity_id = 77485450073 start = 1 end = 10 conn = psycopg2.connect(host="localhost", database="garmin_data", user="postgres", password="******") df = pd.read_sql_query("""select * from (select record_id, power, heart_rate, rank () over (order by timestamp asc) as rank_no from record where activity_id = {}) tbl where tbl.rank_no between {} and {}""".

format(activity_id, start*60,end*60), conn)

Пример кадра данных с данными начального интервала прогрева:



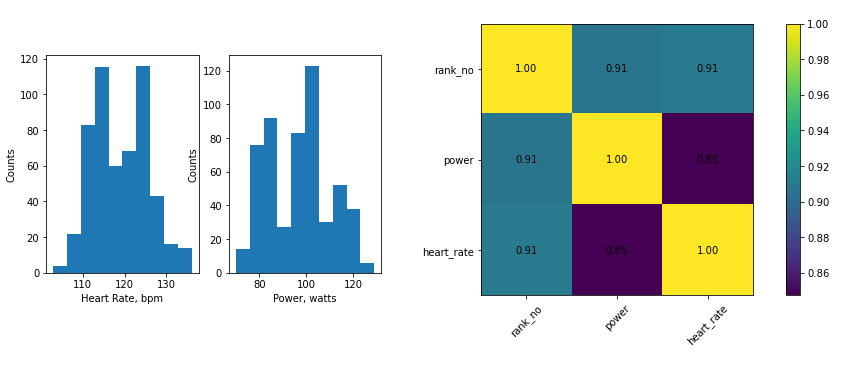
Прежде чем приступить к построению модели, я убедился, что данные из датафрейма имеют нормальное распределение (или похоже на него), нет шума, и рассчитал парный коэффициент корреляции (для power, heart_rate он оказался равным 0,85) .

import pandas as pd import psycopg2 import matplotlib.pyplot as plt activity_id = 77485450073 start = 1 end = 10 conn = psycopg2.connect(host="localhost", database="garmin_data", user="postgres", password="afande") df = pd.read_sql_query("""select rank_no, power, heart_rate from (select record_id, power, heart_rate, rank () over (order by timestamp asc) as rank_no from record where activity_id = {}) tbl where tbl.rank_no between {} and {}""".

format(activity_id, start*60,end*60), conn) fig, (ax1, ax2) = plt.subplots(1,2) plt.rcParams['figure.figsize'] = [12, 5] ax1.hist(df.heart_rate) # ax1.title('Heart Rate values distribution') ax1.set_xlabel("Heart Rate, bpm") ax1.set_ylabel("Counts") ax2.hist(df.power) ax2.set_xlabel("Power, watts") ax2.set_ylabel("Counts") plt.show() # Correlation matrix import numpy as np from mlxtend.plotting import heatmap cm = np.corrcoef(df.values.T) hm = heatmap(cm, row_names=df.columns, column_names=df.columns) plt.show()





Для расчета модели линейной регрессии я использовал модуль Python Статистическая модель и самый распространенный метод Обыкновенный метод наименьших квадратов (OLS) :

import statsmodels.api as sm X = df[['power']] y = df['heart_rate'] X = sm.add_constant(X) model = sm.OLS(y, X).

fit() predictions = model.predict(X)

Используя вычисленные коэффициенты k, я создал график, показывающий распределение значений частоты пульса ( ЧСС [уд/мин] ) в зависимости от мощности ( Мощность [ватт] ), а также добавил линию регрессии.

import matplotlib.pyplot as plt import numpy as np plt.scatter(df.power, df.heart_rate, marker='o', label='record_id', s=8) plt.suptitle('Power and Heart Rate relation fitted line plot', fontsize=14) plt.title('HR[bpm] = {}+{}*Power[watts]'.

format(round(model.params[0],2), round(model.params[1],2)), fontsize=10) plt.rcParams['figure.figsize'] = [6, 6] plt.plot(df.power, model.params[0]+model.params[1]*df.power, color='red') plt.xlabel("Power, watts") plt.ylabel("HR, bpm") plt.show()





Анализ ключевых параметров расчетной модели ( R в квадрате = 0,718, SE = 0,011, р<0.05, F=1372 ), можно заключить, что уравнение ЧСС [уд/мин] = 78,25+0,42*Мощность [Вт] хорошо описывает взаимосвязь между двумя переменными.

Используя описанный метод, я рассчитал модели для остальных 27 тренировок, распределенных по сезону.

Средний коэффициент детерминации для всех моделей превысил значение 0.64 .

Отобразив все полученные значения коэффициента k на графике, можно сделать вывод, что указать разницу между первым и прошлым месяцем или определить тенденцию в динамике не представляется возможным - значения коэффициента k изменяются.

без определенной закономерности на протяжении всего тренировочного сезона.

import matplotlib.pyplot as plt plt.plot(ds.date, ds.coeff, marker="D", linestyle="", alpha=0.8, color="r", label='k on the date') plt.axhline(y=ds.coeff.mean(), color='red', linestyle=':', label='mean value for k') plt.rcParams['figure.figsize'] = [12, 4] plt.title('Distribution of Power coefficient (k) during the training season (HR[bpm] = b+k*Power[watts])') plt.legend() plt.show()





Обратите внимание, что более высокое значение коэффициента k коррелирует с более низкой (худшей) формой обучения.

Другими словами, при низкой форме тренировки при том же увеличении мощности частота сердечных сокращений увеличится больше по сравнению с высокой (лучшей) формой тренировки.

Сравнение коэффициента зависимости частоты и мощности пульса от интенсивности тренировки

Расчет показателя тренировочного стресса

TSS позволяет оценивать тренировки на основе их относительной интенсивности, продолжительности и частоты упражнений.

Значение TSS рассчитывается по следующей формуле:



В формуле: сек – продолжительность тренировки в секундах, NP – нормированная мощность, IF – коэффициент интенсивности [IF = NP/FTP], FTP – значение FTP (в данном случае пороговое значение мощности в ваттах).

Для определения значения ТСС необходимо дополнительно ввести понятие нормализованная мощность (NP) как метод усреднения затрачиваемой мощности для компенсации различий в условиях тренировки (интервалов).

Подробнее о том, как рассчитывается показатель NP, можно прочитать здесь.

Здесь .

Значения TSS для всех тренировок, где доступен FTP, я рассчитал с помощью функций Python:

def normalized_power(activity_id): df = pd.read_sql_query("""select power, rank () over (order by timestamp asc) as rank_no from record where activity_id = {}""".

format(activity_id), conn) WindowSize = 30; # second rolling average NumberSeries = pd.Series(df.power) NumberSeries = NumberSeries.dropna() Windows = NumberSeries.rolling(WindowSize) Power_30s = Windows.mean().

dropna() PowerAvg = round(Power_30s.mean(),0) NP = round((((Power_30s**4).

mean())**0.25),0) return(NP) def tss(activity_id, ftp, NP): sec = pd.read_sql_query("""select count(*) from record where activity_id = {}""".

format(activity_id), conn).

iloc[0][0] TSS = (sec*NP*NP/ftp)/(ftp*3600) *100 return(TSS) conn = psycopg2.connect(host="localhost", database="garmin_data", user="postgres", password="******") tss_df = pd.read_csv('power_zones_data_rf_comparison.csv', index_col=0) tss_df['NP'] = tss_df.apply(lambda row: normalized_power(row['activity_id']), axis=1) tss_df['TSS'] = tss_df.apply(lambda row: tss(row['activity_id'], row['power_threshold'], row['NP']), axis=1)

Объединим набор данных с рассчитанным значением TSS с предыдущим, где хранятся параметры моделей линейной регрессии, и выделим поля дата, TSS, коэффициент для окончательного набора данных:

import pandas as pd df_1 = pd.read_csv('tss.csv', index_col=0) df_2 = pd.read_csv('results.csv', index_col=0) df_1 = df_1.merge(df_2, left_on ='activity_id', right_on = 'activity_id', how='left') df = pd.read_csv('merged.csv', index_col=0) df = df.loc[df.timestamp > '2020-12-26'] df = df.loc[df.timestamp < '2021-04-01'] df['date'] = pd.to_datetime(df['timestamp']).

dt.date df = df[['date', 'TSS', 'coeff']]

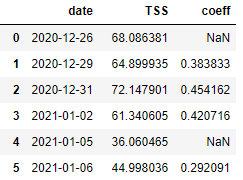
Расчет экспоненциальной скользящей средней

Этот метод используется при оценке состояния спортсмена в планах.

Тренировочные пики .

Давайте создадим новый набор данных дс , где количество строк будет совпадать с разницей в днях между последней и первой тренировкой выбранного периода.

В моем случае это 95 дней (с 26 декабря 2020 по 30 марта 2021 включительно):

import datetime base = datetime.datetime.today() base = max(df.date) date_list = [base - datetime.timedelta(days=x) for x in range(95)] ds = pd.DataFrame({'date': date_list})

Давайте объединим новый набор данных с предыдущим, используя левое соединение, и посчитаем значение EMA для каждой даты, даже если тренировок не было:

ds = pd.merge(ds, df, on='date', how='left') ds = ds.sort_values(by='date') ds['TSS'] = ds['TSS'].

fillna(0) ds['ewm'] = ds['TSS'].

ewm(span=7).

mean()

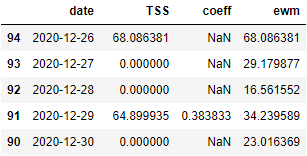
Анализ результатов

join(['Distribution of Power coefficient (k) during the training season', 'in comparison to TSS and EMA for TSS with 7-days span']), y=0.95, x=0.45) fig.legend(loc='center', bbox_to_anchor=(0.4, 0), shadow=False, ncol=2) plt.show()





Анализируя график, не удается выявить каких-либо явных закономерностей, однако стоит отметить зависимость коэффициента k от курса EMA. В целом, можно предположить, что наличие дней отдыха или восстановления перед тренировочным днем приведет к более низкому значению k (или лучшей форме тренировки), и наоборот – к проведению высокоинтенсивных или нескольких тренировок средней интенсивности перед тренировочным днем.

тренировочный день приведет к более высокому значению k (или лучшей форме тренировки).

худшая форма обучения).

Полученные результаты

Конечно, на данном этапе анализа и при имеющемся наборе данных в данном случае получить прямые выводы и закономерности не представляется возможным.

Для более четкого и точного анализа эффективности тренировочного сезона я бы попробовал проводить отдельные тесты в будущих сезонах (например, полностью следуя стандартному протоколу PWC170) в качестве дополнения к обычному тренировочному плану.

Доступен проект Git с примерами кода.

связь .

Теги: #python #Визуализация данных #машинное обучение #анализ данных #garmin #matplotlib #statsmodels #линейная регрессия #велосипед #strava

• Great Plains Consulting: Часто Задаваемые Вопросы По Методологии, Сертификации, Настройке

  19 Oct, 24

• Узнайте, Как Конвертировать Видео В Формат Avi.

  19 Oct, 24

• Состояние Мировой Науки: Сша И Европа Впереди Всех, Но Китай Их Быстро Догоняет

  19 Oct, 24

• Бионический Человек

  19 Oct, 24

• Робот-Собака Еще Не Кусает, Но Уже Предупреждает О Несанкционированном Доступе В Дата-Центр

  19 Oct, 24

• Rss: Убийца Электронного Маркетинга?

  19 Oct, 24

• Оптическое Кольцо Высокой Доступности

  19 Oct, 24

• Операционная Система На Ваш Выбор...

  19 Oct, 24

• Global Devops Bootcamp 2019 В Москве

  19 Oct, 24

• Через Год После Покупки Auto.ru «Яндекс» Планирует Сконцентрироваться На Нерекламной Монетизации Сервиса

  19 Oct, 24