Анализ Данных. Примерные Наборы

Я решил создать серию постов об анализе данных.

В этой (и, как оказалось, очень интересной) области информатики я работаю уже несколько лет. Предлагаю вашему вниманию анализ данных с точки зрения теории приближенных множеств.

О чем мы будем говорить?

Он основан на утверждении, что с каждым объектом мироздания мы связываем некоторую информацию (данные, знания).

Объекты, характеризующиеся одинаковой информацией, неотличимы (сходны) с точки зрения имеющейся о них информации.

Генерируемое таким образом соотношение неотличимости является математической основой теории приближенных (грубых) множеств.

Основу понятия приближенной теории множеств составляют операции аппроксимации множеств.

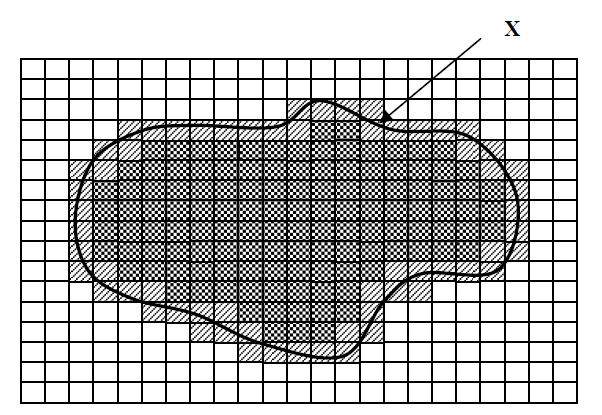
Дадим теперь понятие аппроксимации приближенных множеств:

• Нижнее приближение установить Х
  
  
  
  включает элементы, которые действительно принадлежат множеству X.
• Верхнее приближение установить Х
  
  
  
  +
  
  
  
  включает элементы, которые, возможно, принадлежат множеству X.
• Граница (разница между верхним и нижним приближением)
  
  
  
  представляет собой область неразличимости.

Собственно приложение

Таблица решений представляет собой тройку T = (U, C, D), где U – множество объектов, C — набор атрибутов состояния, D — набор атрибутов решения.

Пример таблицы

Анализ таблицы

• С _Да = {1, 2, 3, 4}
• С _Нет = {5, 6, 7, 8}
• S = {{1, 2, 3, 4}, {5, 6, 7, 8}}

• С _{нормальный} = {1, 3}
• С _{высокий} = {2, 5, 7}
• С _{очень высоко} = {4, 6}
• S = {{1, 3}, {2, 5, 7}, {4, 6}}

• С _Да = {2, 6, 7, 8}
• С _Нет = {1, 3, 4, 5}
• S = {{2, 6, 7, 8}, {1, 3, 4, 5}}

Над чем мы будем работать?

• Алгоритм принятия решений, состоящий из правил принятия решений типа «ЕСЛИ… ТО…».

• Алгоритм LEM, LEM2 [Гржимала-Буссе, 1992] для генерации правил принятия решений типа «ЕСЛИ.

  ТО.

  »

• Red Hat Linux — Технология, Преобразующая Соединения

  19 Oct, 24

• Хорошая Организация, Секрет Успешной Компании

  19 Oct, 24

• Как Построить Процесс Разметки Электронной Торговли, Чтобы Получить Все Необходимые Данные

  19 Oct, 24

• Buffer, «Самая Открытая Компания В Мире», Сократила 11% Своего Персонала

  19 Oct, 24

• Создание Интерфейса Для Игры

  19 Oct, 24

• Роботизированная Рука Curiosity Сможет Продолжить Работу На Следующей Неделе

  19 Oct, 24

• Фриланс – Это Практика. 4 Года Спустя

  19 Oct, 24

• Поговорим О Взаимодействии С Фрилансерами №2

  19 Oct, 24

• На Каком Языке Вы Бы Написали Матрицу?

  19 Oct, 24

• Отличный Спам-Бот! :)

  19 Oct, 24