В задаче о суперстроках, учитывая входной набор строк, вам нужно найти самую короткую строку, содержащую каждую из них в качестве подстроки.
Эта проблема возникает в различных приложениях, например, при сборке генома или сжатии данных.
Эта задача NP-трудна, поэтому рассчитывать на эффективный алгоритм поиска точного решения нельзя.
Максим Николаев — аспирант ПОМИ РАН, преподаватель Центра информатики и СПбГУ, преподаватель математики лицея № 533 в Санкт-Петербурге.
В 2019 году окончил центр КС по специальности «Современная информатика».
В статье ниже Максим рассказывает о своей исследовательской работе во время обучения поиску приближенных решений проблемы суперструн.

Жадная гипотеза
Как и в других NP-трудных задачах, в задаче о суперструнах представляют интерес и активно исследуются приближенные алгоритмы, быстро находящие достаточно точное решение.
Лучший полиномиальный алгоритм, известный на сегодняшний день, находит суперстроку не более
раз дольше, чем точное решение.
При этом уже более 30 лет остается нерешенной так называемая жадная гипотеза, которая гласит, что элементарный жадный алгоритм «выбирает две строки с максимальным пересечением и объединяет их; продолжайте делать это, пока не останется только одна строка» — это 2-приближение.
Более подробно о проблеме и возникающих в ней гипотезах можно прочитать в замечательном Открытая лекция Центра CS .
Ниже будет краткое изложение этого и описание моих результатов.
Иерархический граф и суперстроки
В попытке приблизиться к решению жадной гипотезы и разработать более совершенные приближенные алгоритмы группа Александра Куликова разработала теоретико-графовый подход, позволяющий в удобной форме изучать структуру пересечений исходных строк друг с другом.Для этого вводится так называемый иерархический граф, вершинами которого являются исходные строки и все их возможные подстроки, а ориентированные ребра идут от префикса каждой строки к этой строке и от строки к ее суффиксу.
Префикс и суффикс строки — это строки, полученные удалением последней и первой буквы строки соответственно.
Вершины графа удобно расположить по уровням в зависимости от длины соответствующих линий, поэтому граф называют иерархическим.
На рисунке ниже показан иерархический граф для исходного набора строк {aaa, cae, aec, eee}, которые изображены прямоугольниками.
Пустая строка обозначается
.
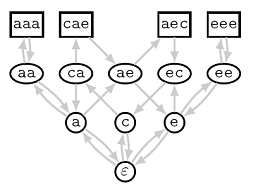
Где здесь надстройки? Суперструны в этом графе соответствуют циклам, проходящим через
и все исходные вершины.
Для каждого такого цикла можно восстановить суперструну, и наоборот. Например, на рисунке ниже показан цикл, соответствующий суперстроке aaaecaeee. В этой суперстроке исходные строки располагаются в порядке ааа
АЭК
ЦЕ
эээ, и именно в таком порядке по ним проходит упомянутый цикл.
Легко показать, что длина суперстроки всегда равна количеству стрелок вверх в соответствующем цикле (в примере их 9).
Это означает, что проблема поиска кратчайшей суперструны превращается в проблему поиска кратчайшего цикла в иерархическом графе.
Жадный иерархический алгоритм и схлопывающийся алгоритм
Естественно, такая замечательная структура, как иерархический граф, требует разработки на ее основе интересных алгоритмов.Моей задачей было изучить два таких алгоритма.
Первый из них, Жадный иерархический алгоритм (GHA), по-видимому, является самым простым способом построения цикла по исходным вершинам, который может претендовать на роль хорошего приближения точного решения.
Как следует из названия, он жадный и кратко его можно описать так: пройдемся по уровням графа сверху вниз, а внутри уровня по всем вершинам в лексикографическом порядке; для каждой из вершин, во-первых, обеспечиваем равенство степени входа и выхода (чтобы решение представляло собой цикл), добавляя подходящее количество ребер между текущим уровнем и нижним, а во-вторых, если вершина исходного или если оно является последним в лексикографическом порядке по вершине какой-либо уже построенной циклической компоненты (ребра которой лежат выше заданного уровня), то освобождаем из него два ребра в его префикс и суффикс.
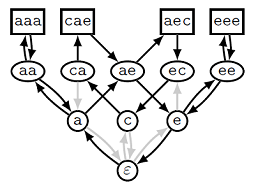
Работа алгоритма для нашего набора данных из предыдущих примеров показана на рисунке ниже.
Легко заметить, что на втором рисунке края aa и ee были освобождены, чтобы гарантировать, что исходные строки aaa и eee соединены с
и ребра из ca и ec, чтобы сбалансировать соответствующие вершины.

Видно, что алгоритм старается добавить как можно меньше ребер — он делает это только для обеспечения цикличности и связности — необходимых условий соответствия цикла некоторой суперстроке.
Второй алгоритм в некотором смысле противоположен первому.
Он называется Collapsing Algorithm (CA), и если GHA начинает с пустого графа и добавляет ребра только при необходимости, то CA начинает с какого-то решения и пытается удалить из него ненужные ребра.
Удаление ненужных ребер происходит следующим образом: алгоритм движется по графу сверху вниз, обходя вершины на каждом уровне в лексикографическом порядке; если для некоторой вершины
в цикле есть "галка"
, то алгоритм пытается его «свернуть» (следовательно Collapsing), заменив на «галку»
, но только если это не нарушит связность цикла.
Если
находится на первом уровне, то этот флажок просто удаляется.
Таким образом, алгоритм пытается сбросить все лишние пары ребер вниз, а затем удалить их.
Пример СА, работающего над удвоенным оптимальным решением (удвоение необходимо для получения дополнительных ребер), можно увидеть на рисунке ниже.
Различные гипотезы
Моей задачей было изучить описанные алгоритмы с целью доказать или опровергнуть любую из описанных ниже гипотез.Гипотеза о коллапсе гипотезы - возьмите любое решение, удвойте его ребра и подайте на вход CA. Полученный результат не зависит от первоначального решения! Если эта гипотеза верна, то мы имеем очень простой алгоритм 2-приближения: берем любое решение (например, тривиальное, полученное путем объединения всех исходных строк), удваиваем ребра в нем и схлопываем.
Конечный результат такой же, как если бы вы удвоили и свернули оптимальное решение.
Но если это так, то полученный результат не более чем в два раза дольше оптимального.
Жадная иерархическая гипотеза – граф, возникающий в результате коллапса любого удвоенного решения, является именно тем графом, который строит ГСГ! Эта гипотеза была проверена на очень большом количестве случайных и неслучайных наборов исходных строк, но контрпример найти не удалось.
В частности, для приведенных выше примеров, иллюстрирующих работу ГСГ и СА, гипотеза верна.
Из этой гипотезы сразу следует, что ГСГ является 2-приближением.
Слабая жадная иерархическая гипотеза - ГСГ является 2-приближением.
Даже если предыдущие две гипотезы ложны, то ГСГ всё равно может быть 2-приближенным.
Моя работа
Первое, что меня заинтересовало: как ГСГ связан с обычным жадным алгоритмом? В некоторых примерах ГСГ строит более короткое решение, но всегда ли это происходит? Можем ли мы показать, что ГСГ столь же жадный? Как описать жадный алгоритм с помощью иерархического графа? Как увидеть момент «склеивания» двух линий в одну в иерархическом графике? В процессе проработки всех этих вопросов я выяснил, что ГСГ на самом деле является частным случаем обычного жадного алгоритма! Дело в том, что жадный алгоритм недетерминирован: в его описании не оговаривается, что произойдет, если имеется несколько пар строк с максимальным пересечением.Предполагается, что алгоритм может выбрать произвольную пару, а это означает, вообще говоря, что даже на одном и том же наборе данных он может выдавать разные решения.
ГСГ по своей сути является неким определением алгоритма — его определение включает точный порядок, в котором будут объединяться пары строк, поэтому одно и то же решение всегда строится из заданного набора исходных строк.
Это свойство означает, что жадная гипотеза подразумевает 2-аппроксимацию ГСГ, поэтому, строго говоря, доказательство слабой жадной иерархической гипотезы должно быть проще, чем жадной гипотезы.
Также оказывается, что это определение не лучше исходного алгоритма — есть примеры, на которых ГСГ работает хуже, чем какое-то другое жадное определение.
Следующий этап моего исследования был посвящен более детальному изучению работы ГСГ над набором данных, в котором длина всех строк ограничена некоторой константой.
Если эта константа равна 2, то ГСГ точен, а сама проблема, следовательно, из класса P, и начиная с максимальной длины 3, проблема становится NP-полной и для этого случая уже не было ясно, насколько приблизителен ГСГ.
Для случая строк длины не более 3 я показал, что ГСГ является 1,5-приближением и эта оценка асимптотически точна, т.е.
для любого
вы можете предоставить набор данных, на котором ГСГ построит решение
раз дольше, чем точный.
К сожалению, на случай строк длины 4 и более мне ничего придумать не удалось, и я решил переключиться на изучение остальных гипотез.
Во-первых, поработав над строками длиной не более 3, я решил попробовать разобраться в жадной иерархической гипотезе для этого случая, и мне это удалось.
Более того, был доказан ещё более сильный результат: чтобы всё разрушилось, в ГСГ нет необходимости удваивать всё решение — достаточно добавить к решению произвольное покрытие исходных вершин циклами (которые уже не являются необходимые для образования одного связного цикла).
Во-вторых, я выяснил, что если в общем случае к решению, полученному ГСГ, приклеить произвольный набор циклов (например, само решение ГСГ подходит), а затем все свернуть, то мы снова получим ГСГ.
Это означает, что гипотеза о коллапсе следует из гипотезы жадной иерархии.
Поскольку обратное следствие очевидно, то оказывается, что эти две гипотезы эквивалентны.
ПРИБЛИЗИТЕЛЬНО 2019 ГОДА Конференция
Все полученные результаты, за исключением приближения 1,5, были включены в статья Гипотеза о коллапсе суперструн , который был принят на конференцию APPROX 2019 и опубликован в ее сборнике.Это одна из ведущих конференций по приближенным алгоритмам, что говорит об актуальности темы и интересе к ней среди научного сообщества, несмотря на то, что ни одна из гипотез не доказана и не опровергнута.
Дальнейшая работа
Окончив центр, я до сих пор периодически возвращаюсь к этой задаче.По состоянию на осень 2020 года ни об одной из гипотез ничего определенного неизвестно, но более глубокое понимание проблем, препятствующих их решению, все же появляется.
Если эта задача покажется интересной, вы можете обратиться Александр Куликов для получения актуальной информации и подробных комментариев.
Теги: #Алгоритмы #Центр CS

-
Как Ни Странно - Крысолов
19 Oct, 24 -
Производительность Gridfs
19 Oct, 24


