Наконец, о второй части доклада Сурьи Гангули - как теоретическое понимание процесса оптимизации может помочь на практике, а именно, какую роль играют седловые точки (первая часть здесь) здесь , и это совершенно необязательно для дальнейшего чтения).

Отказ от ответственности: этот пост основан на отредактированных журналах чата.
closecircles.com , отсюда и стиль изложения и уточняющих вопросов.
Напомню вам немного, что такое седловые точки.
В пространстве нелинейных функций существуют точки с нулевым градиентом по всем координатам — именно к этим точкам стремится градиентный спуск.
Если точка имеет градиент 0 по всем координатам, то это может быть: 
- Локальный минимум, если вторая производная положительна во всех направлениях.
- Локальный максимум, если вторая производная отрицательна во всех направлениях.
- Седловая точка, если вторая производная положительна в одних направлениях и отрицательна в других.
- Во-первых, подавляющее большинство точек с нулевым градиентом являются седловыми точками, а не минимумами.
Это легко понять интуитивно – чтобы точка с нулевым градиентом была локальным минимумом или максимумом, вторая производная должна быть одного знака.
во всех направлениях , но чем больше измерений, тем больше шанс, что хотя бы в каком-то направлении знак будет другим.
И поэтому большая часть сложных точек, с которыми придется столкнуться, будут седловыми.
- Во-вторых, с увеличением количества параметров оказывается, что все локальные минимумы достаточно близки друг к другу и к глобальному минимуму.
В сотрудничестве с лабораторией Йошуа Бенджио им удалось экспериментально продемонстрировать их для нейронных сетей (теоретически они их пока не освоили).
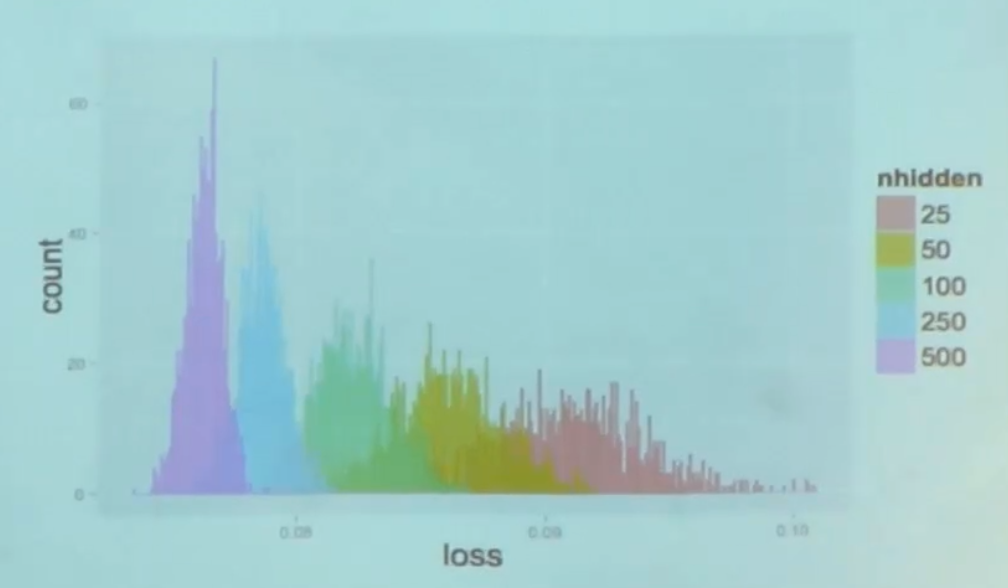
Это гистограмма значений функции стоимости в локальных минимумах, полученных в результате множественных попыток обучения из разных точек — чем меньше параметров, тем меньше разброс значений в локальных минимумах.
При большом количестве параметров разброс резко уменьшается и становится очень близким к глобальному минимуму.
Главный вывод – не надо бояться локальных минимумов; основные проблемы связаны с седловыми точками.
Раньше, когда у нас плохо получалось обучение нейронных сетей, мы думали, что это потому, что система скатывается к локальному минимуму.
Оказывается нет, мы просто не смогли выйти из седловой точки.
И поэтому они придумали настройку градиентного спуска, которая позволяет хорошо избегать седловых точек.
К сожалению, там используют гессен.
Для необразованных вроде меня гессиан — это матрица значений попарных вторых производных в точке.Конечно, вычисление гессиана для современных нейронных сетей ужасно непрактично, поэтому я не знаю, как применить их решение на практике.Если вы думаете о градиенте как о первой производной функции многих переменных, гессиан — это вторая.
Александр Власов Здесь написал хороший руководство о так называемых оптимизациях второго порядка, к которым относится работа с гессианом.
Второй момент — они придумали некую теоретически кошерную инициализацию, которая в случае просто линейных систем решает проблему исчезновения градиентов и позволяет обучать сколь угодно глубокую линейную систему за то же количество градиентных шагов.
И говорят, что это помогает и нелинейным системам.
Однако я пока не встречал в литературе упоминаний об успешном использовании этой методики.
Ссылки на полные статьи: об оптимизации градиентного спуска И об улучшенной инициализации .
Мы живем в интересные времена.
Теги: #глубокое обучение #невыпуклая оптимизация #Машинное обучение

-
Компьютерная Безопасность – Что Это Такое?
19 Oct, 24 -
Все О Toshiba Satellite P505-S8020
19 Oct, 24 -
Вы Читали Кнута?
19 Oct, 24 -
О Серебре На Стыке Физики И Истории
19 Oct, 24 -
Modx. Основные Вещи
19 Oct, 24 -
О Маленькой Ос
19 Oct, 24


