В данной статье мы продолжаем обзор свойств внешней алгебры.
В первая часть мы определили внешнее произведение элементов, ввели понятия симплексов, границ и коспространства.
Здесь мы рассматриваем аффинные пространства, в которых определено скалярное произведение между элементами.
Такие пространства еще называют евклидов .
Окружающее нас трехмерное пространство вполне подходит в качестве евклидова пространства.
У него есть скалярное произведение как между элементами, так и между векторами.
Но все же это лишь частный случай общего семейства пространств.
Чаще встречаются пространства, в которых уточняются соединения элементов, в просторечии называемые графики .
Поэтому начнем с описания графиков.
Покажем, как построить полиформу для заданного графа и на ее основе определить ее метрические свойства.
Полиформа графа строится на основе его связей.
Но можно пойти и другим путем – от расстояний между элементами.
Вот как полиформа строится на обратных элементах; мы кратко рассмотрим это в конце.
Обновление.
Прежде чем читать эту статью, лучше ознакомиться со следующим: эта часть , если еще не.
Билинейные и квадратичные формы
Поскольку евклидово пространство обладает дополнительным (по отношению к просто аффинному) свойством, нам необходимо определить сущность, выражающую это свойство.Мы должны дать возможность настройка соединений между элементами пространства.
Это можно сделать с помощью билинейная форма , которую мы в дальнейшем будем называть просто формой.
Что такое «форма»? Легче всего думать о ней как о еще одном Тип работы .
Аргументами вида (множителями произведения) могут быть произвольные цепочки (или коцепи).
Обычно порядок аргументов формы тот же.
Напомним, что цепи представляют собой линейные комбинации симплексов — внешних произведений элементов.
Здесь аргументами формы будут в основном границы (поливекторы).
Формы будем обозначать угловыми скобками.
Вот пример билинейной формы, образованной двумя векторами.
И
:
Вместо круглых скобок можно было бы использовать какой-нибудь знак умножения, но возникают трудности с выбором подходящего символа, а для обозначения форм общеприняты угловые скобки.
И еще — внутри формы мы опустили круглые скобки для обозначения границ (векторов).
То есть
.
Далее мы будем иметь дело в основном с границами и не хотим обременять выражение слишком большим количеством круглых скобок.
Почему форма билинейный ? Приставка «би» здесь означает, что форма имеет два аргумента — ее валентность (или ранг) равна двум.
А линейный это потому, что оно подчиняется закону дистрибутивности, как и любое произведение, то есть линейно в своих аргументах.
Если какой-либо аргумент формы является суммой, то форму можно представить как сумму форм.
Вы также можете извлечь скалярный коэффициент (или знак) из аргументов:
Если форма является продуктом аргументов, то каков ее результат? Это хороший вопрос, ответ на который: форма – это результат труда.
То есть форма просто связывает (объединяет) свои аргументы.
Эта форма аналогична внешней работе.
Но, напротив, аргументы формы могут быть одним и тем же элементом.
Такие формы называются квадратичный (иногда квадратный).
Чтобы не повторять одно и то же рассуждение дважды, будем обозначать квадратичные формы по степени:
Здесь мощность — всего лишь напоминание о том, что форма квадратная.
Важной особенностью квадратичной формы является то, что она не зависит от знака аргумента.
То есть избавляет от необходимости следить за знаком аргументов:
.
Кстати, перестановка аргументов формы называется ее транспозиция
.
В общем, форма и ее транспозиция — это разные формы! Теперь внимание.
Фигуры можно умножать и складывать.
Сложение мы уже видели, а как насчет умножения? При перемножении двух форм перемножаются их аргументы - лево с левым, право с правым.
Пожалуй, это главное свойство форм.
Умножение аргументов — это их внешний продукт. Тот, который мы рассматривали в предыдущая часть .
Следовательно, если перемножаемые границы (аргументы) имеют общую вершину, то они сливаются в одну:
Порядок результата произведения равен сумме порядков перемножаемых форм (порядок формы — это порядок ее аргументов).
Важно, что произведение форм коммутативно .
Как было показано в первой части, знак произведения двух симплексов при их перестановке зависит от четности произведения их порядков.
Но так как форма имеет два аргумента, то если изменится знак левого аргумента, то точно так же он изменится и у правого.
Это следует из того, что оба аргумента формы имеют одинаковый порядок.
Минус за минусом даст плюс, то есть знак формы останется прежним:
.
Подобно тому, как существует единичный симплекс, существует и тождественная (единичная) форма, при умножении на которую произвольная форма не меняется:
.
Нулевая форма также существует. Более того, если один из аргументов формы равен нулю, то и вся форма равна нулю — это полезное свойство, позволяющее сократить многие выражения.
Полиформы
Линейную комбинацию форм будем называть полиформой – это сумма форм, каждая из которых умножается на определенный скалярный коэффициент. Пример полиформы на трех вершинах:Каждый член полиформы форм-мономиальный определенный порядок.
Форма единицы имеет 0-й порядок – это скалярная форма.
Векторная форма
имеет 1-й порядок и т. д. Члены полиформ можно сгруппировать по порядку их мономиальных форм.
Каждая такая сумма имеет свой порядок (сорт), поэтому такие суммы удобно называть формы оценок .
Если обозначить форму оценки k-го порядка как
, то полиформа — это сумма форм оценок:
Вообще алгебру выражений, содержащую мономы разных порядков, обычно называют закончил .
Поскольку количество терминов растет (а мы только начали), пришло время заземлиться и привязать абстрактные полиформы к какой-то известной сущности.
Определений достаточно, чтобы представить полиформу общения.
Вот связь между двумя элементами (это граф из двух вершин): 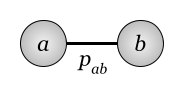
Связь между двумя элементами и вот его полиформа:
.
Здесь
- скаляр, величина связи.
Его значение отражает близость элементы
.
Если обозначить размерность линейных расстояний как
(длина), то размер соединения будет
, (квадрат появляется, потому что форма квадратная).
Почему полиформа соединения выглядит именно так? Никто не знает (шучу).
Будем считать, что это установлено эмпирически.
В простых графах связи равны единице, поэтому полиформа единичной связи имеет вид
.
Мы также будем называть полиформу связи факторная форма , - тогда станет понятно почему.
Факторная форма обладает интересным свойством — умножение факторной формы на саму себя эквивалентно удвоению величины связи:
Или вообще:
.
Отсюда уже можно догадаться, какую форму имеет полиформа двух разных связей.
Пусть значение связей равно 1 (коэффициенты всегда можно добавить), тогда последовательное соединение трёх вершин образует граф-путь (маршрут)
.
Полиформа маршрута равна произведению полиформ каждой его ссылки — вот так:
Это факторное представление полиформы графа, то есть произведение факторных форм ее связей.
Можно раскрыть скобки и получить линейное разложение полиформы:
Теперь ясен общий метод получения полиформы графа.
Полиформа графа — это произведение факторформ его связей.
.
Из этого определения следует, что если разделить граф на два подграфа (разделив множество связей графа на два подмножества), то полиформа графа будет произведением полиформ этих подграфов.
Это факториальное свойство полиформы графа.
Чтобы получить полиформу цикла на трех вершинах, нужно добавить в маршрут еще одно соединение.
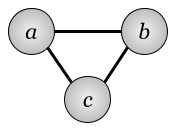
Ненаправленный цикл
В этой полиформе можно выделить три градационные формы: 0-го порядка.
, 1-й заказ
и 2-й порядок
.
Ряд Тейлора (ну почти)
Давайте немного поиграем с полиформой графа.Мы можем изменить его представление, используя тот факт, что умножение мономиальной формы на саму себя дает ноль.
Если возвести в квадрат сумму нескольких форм, результатом будет их двойное произведение по всем возможным комбинациям форм:
Здесь используется коммутативность произведения.
Двойка появляется благодаря тому, что произведение одной формы на другую происходит дважды.
Если возместить сумму фигур в куб, то всего получится 6 произведений фигур – именно столько будет возможных комбинаций разных фигур:
.
Шесть здесь — факториал трёх.
Для 4-й степени получим (если получим) коэффициент 24 = 4! Но полиформа графа состоит именно из произведений всех возможных связей разных порядков.
Отсюда следует, что все формы оценок полиформы-графа можно получить, возведя ее форму оценки 1-го порядка в степень
, который просто представляет собой сумму форм с коэффициентами, равными связям графа.
Назовем эту форму оценки основа полиформы.
База простого цикла из трех вершин равна
.
Тогда полиформа всего графа представляет собой сумму степеней основания с коэффициентами в виде обратных факториалов:
Здесь суммирование ведется от нуля, что означает, что основание в нулевой степени соответствует единичной форме.
Верхний индекс суммирования – это предельная степень (сорт) полиформы, выше которой все степени будут равны нулю.
В принципе, можно было бы его опустить и считать градусы до бесконечности.
Мы не путаем степень основания и градальную форму данного ордена.
Но они связаны, да:
Если сумма градусов вам что-то напоминает, то вы не ошибаетесь.
Точно такой же вид имеет разложение показательной функции в ряд Тейлора.
Только здесь в роли переменной выступает база.
Поэтому полиформу графа можно записать ещё короче:
Не утруждайтесь попытками понять, что означает возведение в степень полиформы — это просто компактная форма записи суммы форм оценок.
Но это красиво, правда? Касательно крайняя степень .
В математике есть понятие индекс нильпотентности , — индекс, при котором степень нильпотентного объекта обращается в нуль.
Но предельная степень удобнее.
Его значение на 1 меньше индекса нильпотентности.
Обозначим число вершин графа и количество независимых компонент, тогда предельная степень будет равна
.
Это также можно выразить через график количества связей и цикломатическое число.
Как
.
Например, для приведенного выше несвязного графа из двух компонент на 4 вершинах предельная степень равна двум (4-2=2).
То есть все полномочия выше второго основания
будет равен нулю.
Итак, для полиформы графа у нас есть два представления.
Один факториал - в виде произведения фактор-формных связей.
Другой добавка - в виде суммы степеней основания, где основанием является сумма форм связей в графе.
Не каждая полиформа с произвольными коэффициентами будет иметь факторное представление, так же как не каждый многочлен можно разложить в произведение многочленов более низкого порядка.
Разложимые полиномы называются приводимыми.
В этой терминологии полиформа графа — это управляемый полиформ .
То есть это полиформа, которую можно выразить как произведение полиформ низшего порядка (для графа — как произведение форм 1-го порядка).
Существуют полиформы, которые невозможно разложить на произведение (несводимые).
Вот простейший пример такой полиформы:
Полиформы такого типа описаны гиперграфы .
Это графы, которые могут иметь связи не только между двумя вершинами, но и между тремя, четырьмя и т. д. Поэтому полиформа — более общий механизм описания графов (и пространств), чем, например, матрица смежности.
Форма лимита и номер ядра
Пришло время разобраться — что именно дает представление графа в виде полиформы? Как это использовать? Сама полиформа задается через значения соединений.Но эти связи преобразуются полиформой в метрические характеристики пространства — расстояния между вершинами графа, углы между векторами, площади треугольников и т. д. По сути, полиформа представляет собой (или заменяет) метрический тензор.
В первой части мы представили понятие лимит лимит для конечного набора элементов: .
Это соответствует предельная форма
.
Предельная форма на 4 вершины
имеет 3-й порядок и равен
.
Поскольку граф обычно имеет конечное множество вершин, он также имеет предельную форму.
Произведение любой мономиальной формы полиформы графа и ее предельной формы дает ноль (поэтому оно предельное).
Коэффициент предельной формы полиформы графа называется основной номер (номер дерева) граф.
То есть градационная форма предельной степени может быть выражена как
, где – номер охвата графа.
В теории графов остовное число интерпретируется как количество различных скелеты (деревья) , который можно построить по связям заданного графа.
В графе путей остовное число равно 1 (путь — это одно дерево), в графе циклов — это количество связей (удаляя по одному звену цикла, мы получаем разные деревья).
Почему коэффициент предельной полиформы равен числу возможных деревьев, понять не так уж и сложно.
В первая часть Мы представили правило слияния границ при умножении, из которого следует, что одну и ту же границу можно получить слиянием разных границ более низкого порядка.
Полиформа графа формируется путем умножения факторных форм, образованных связями.
Чем больше связей умножается, тем выше порядок результирующей фигуры (и границы).
Более того, одну и ту же форму можно получить перемножением разных форм.
Поэтому коэффициент для него будет отражать количество способов, которыми исходные связи (векторы) могут быть объединены в одну общую границу.
Например, в 3-цикле количество таких способов равно трем, поскольку здесь три соединения с общей вершиной перемножаются попарно.
Номер ядра произвольной полиформы обозначим как
.
Затем
Число ядер графа из 3 узлов с произвольным значением связей можно выразить явно:
.
Его размерность обратна четвертой степени расстояния.
В общем случае числовое остовное число обратно пропорционально квадрату объема k-мерного симплекса, образованного вершинами графа:
Откуда можно вывести выражение квадрата площади треугольника через связи между вершинами:
Граф связен, если его полиформа содержит предельную форму для данного набора вершин.
Не все графы имеют ненулевое число охвата, и не все полиформы содержат ограничивающую форму.
Если граф состоит из несвязных компонент, то он не имеет предельной формы, что эквивалентно нулевой связности графа.
Пример минимального несвязного графа — две компоненты двух вершин:
Потенциалы форм
Давайте посмотрим на другие характеристики.Каждая форма может быть связана со значением внутри данной полиформы.
Звучит расплывчато, поэтому давайте уточним.
Если есть определенная полиформа (например, полиформа графа цикла) и есть некоторая форма (например, векторная форма
, то для данной формы вы можете вычислить ее скалярное значение внутри полиформы.
Назовем эти величины потенциалами формы.
Как рассчитать потенциал фигуры? Это не сложно — умножаем полиформу на форму и находим коэффициент предельной формы результата.
Это будет потенциал формы.
Вот формальное выражение потенциала фигуры в полиформе:
Номер ядра графа соответствует потенциалу единичной формы:
.
Потенциал предельной формы равен 1; при умножении полиформы на предельную все одночленные формы, кроме единичной, обнуляются:
.
Рассчитаем векторный потенциал
для графа путей.
Умножив векторную форму на полиформу пути, мы получим:
Теги: #математика #графы #фигуры #алгебра #евклидово пространство #Внешнее произведение
-
Аренда Видеоигр: Лучше, Чем Когда-Либо
19 Oct, 24 -
Hmi На Базе Node-Red И Scadavis.io
19 Oct, 24 -
Теперь Yahoo — Полноценная Социальная Сеть
19 Oct, 24 -
Аудиофильский Патчкорд
19 Oct, 24


