Вероятностное моделирование — один из самых мощных инструментов для специалиста по данным.
К сожалению, чтобы его использовать, необходимо не только уверенно разбираться в теории вероятностей и математической статистике, но и знать детали того, как работают алгоритмы приближенного байесовского вывода, что делает барьер для входа очень высоким.
В этой лекции вы познакомитесь с относительно молодой парадигмой машинного обучения — вероятностным программированием.
Его цель — сделать всю мощь вероятностного моделирования доступной каждому, у кого есть опыт программирования и минимальный опыт анализа данных.
Лекцию читал Борис.
хр0никс Янгеля на факультете компьютерных наук, открытом в Высшей школе экономики при поддержке Яндекса.
Сам Борис окончил факультет вычислительной математики и кибернетики МГУ и Школу анализа данных Яндекса.
Работал в Microsoft Research Cambridge в группе Кристофер Бишоп выше рамок Инфер.
NET .
Сейчас Борис — ведущий разработчик поиска Яндекса.
Ниже приведена стенограмма рассказа.
Моя цель сегодня — рассказать вам, что такое вероятностное программирование и как эта недооцененная парадигма в машинном обучении предоставляет возможности вероятностного моделирования на службу всем, кто умеет программировать и имеет базовые представления о вероятности, математической статистике и моделировании.
основы.
Что именно мы делаем в машинном обучении? На самом деле мы хотим как-то рассуждать о процессах в реальном мире и о том, как эти процессы работают. Есть определенные объекты, которые участвуют в этих процессах.
Например, пользователь, который просматривает результаты поиска и решает, интересен ему результат поиска или нет, кликает на него, просматривает следующий результат или вообще уходит со страницы поиска.
Это пример объектов.
Объекты имеют определенные свойства.
Например, для пользователя это могут быть его непосредственные информационные потребности, его интересы в целом.
Соответственно, существует среда, в которой существуют эти объекты и которая тоже обладает некоторыми свойствами.
А есть, по сути, сам сложный процесс: процесс подбрасывания монеты или процесс просмотра пользователем результатов поиска, о котором мы и хотим поговорить.
И, как правило, имея какие-то наблюдаемые проявления этого процесса, мы хотим обратить его вспять и понять, какие свойства объектов и среды привели к тому, что мы наблюдали.
Например, после нескольких раз проверки того, выпадет ли монета орлом или решкой, мы хотим знать, честная она или нет. Или, посмотрев несколько раз на то, куда нажал пользователь, мы хотим понять, вышел ли он из поиска счастливым или недовольным, нашел ли он то, что ему нужно, или нет, и были ли документы, которые мы ему показали, актуальны или нет. Здесь есть небольшая проблема.
Сложный процесс, который мы хотим изучить, как правило, довольно проблематично заранее описать, как он происходит. В случае нашего пользователя – это некие сложные биохимические процессы, которые происходят в его мозгу и которые в конечном итоге заставляют его принять то или иное решение.
Понятно, что его обращение — невероятно сложная вычислительная задача (даже если ее можно описать), и никто этого делать не будет. Поэтому мы прибегаем к методике, называемой вероятностным моделированием и заключающейся в следующем.
Сначала мы строим модели объектов, акцентируя внимание только на тех свойствах, которые, по нашему мнению, важны в этом процессе.
И мы игнорируем тех, кто мало на него влияет. Например, мы можем сказать, что монета описывается одним числом ее честности, или мы можем сказать, что пользователь описывается вектором чисел, где каждый компонент вектора показывает его интерес к определенной теме.
Например, первый компонент рассказывает, насколько ему интересно найти видео, второй — насколько ему интересны фотографии с забавными котиками и так далее.
Тогда у нас есть сложный процесс, который мы заменяем некоторой его округленной версией, которая, с одной стороны, имеет что-то общее с тем, что происходит в реальности, но, с другой стороны, достаточно проста в работе.
В нашем гипотетическом примере с пользователем можно было бы сказать, что он просматривает результаты сверху вниз, и если следующий результат удовлетворяет его информационную потребность и коррелирует с его текущими интересами, то он щелкает и останавливается, а если нет, то перемещается.
на.
Здесь сразу возникает небольшая проблема: если мы посмотрим на реальные клики пользователей, то окажется, что модели, которые я только что предложил, неудовлетворительны в том смысле, что модель не может воспроизводить все эти шаблоны кликов, которые мы наблюдаем в реальности.
Например, пользователи иногда кликают на вещи, которые им совершенно не интересны.
Почему? Ему хотелось именно так, а может, он увидел какой-то результат, который его удивил, и ему захотелось щелкнуть и посмотреть, что там произойдет. Соответственно, наша модель не может выдать такие данные, и в этом проблема.
Что делать? Здесь используется хитрость, поэтому эти модели называются вероятностными: мы добавляем немного шума в модель, которая предназначена для моделирования тех сложных явлений, которые мы не можем моделировать напрямую.
Мы считаем, что они настолько сложны, что очень неотличимы от шума, но добавление этого шума позволит нашей модели исключить из себя все возможные наблюдения и тогда можно будет обратить ее вспять.
В примере с пользователем можно сказать, что когда он видит очередной результат, он подбрасывает монетку и в зависимости от того, как она упала, решает, смотреть ли этот результат, понравился ли он ему, или идти дальше, или надоест. и перестаньте смотреть на результаты.
Таким образом, в рамках этой модели становятся возможными все шаблоны кликов.
Хотя некоторые более вероятны.
И построенная модель по-прежнему имеет смысл и коррелирует с реальным физическим процессом, который мы хотим смоделировать.
Если мы построили такую модель, то формально можно сказать, что мы построили совместное распределение вероятностей свойств объектов и наблюдаемых данных.
Тогда мы можем повернуть этот процесс вспять с помощью важной теоремы, которая называется теоремой Байеса и которая говорит нам, как на основе наших априорных знаний об объектах, которые мы хотим изучить, после наблюдения некоторых данных уточнить эти знания и двигаться дальше.
к апостериорному распределению вероятностей.
В этом, в принципе, и вся суть вероятностного моделирования.
К сожалению, существует ряд проблем с вероятностным моделированием.
Саму модель относительно легко разработать для любой предметной области.
Не в том смысле, что легко разработать модель лучше существующей.
Обычно это довольно сложно, потому что в определенных предметных областях люди годами и десятилетиями только и делают, что придумывают модели.
Но если, например, вы столкнулись с каким-то новым процессом, новой предметной областью, которую вы более-менее понимаете и которую хотите моделировать, и у вас есть некоторые базовые представления о том, как вообще строятся вероятностные модели, то придумайте разумная модель, вероятно, не займет много времени.
Может быть, часы или дни.
Затем вам нужно сделать фактический вывод в модели, используя теорему Байеса, чтобы найти апостериорное распределение интересующей переменной в условиях наблюдения.
Ранее было сказано, что теорема Байеса дает вычислительный рецепт, который позволит вам сделать это для любой модели.
С одной стороны, это правда, но с другой стороны, этот вычислительный рецепт может быть очень сложным.
Грубо говоря, просто невозможно вычислительно посчитать все члены теоремы Байеса для более или менее сложной модели.
Поэтому уже несколько десятилетий разрабатываются приближенные методы байесовского вывода, которые позволяют найти некоторую аппроксимацию апостериорного распределения, которая при определенных условиях будет хорошим приближением.
В общем, если вы хотите сделать вероятностный вывод из сложных вероятностных моделей, вам неизбежно придется прибегнуть к таким приближенным методам вывода.
Здесь перечислено несколько таких методов, это EP, VMP, MCMC. Все эти методы достаточно сложны в реализации, концептуальны и не очень просты.
В результате, чтобы написать вывод в какой-то из ваших вероятностных моделей, вам нужно потратить много времени на его понимание.
В то же время по-настоящему сложные модели потребуют знаний уровня доктора философии в области машинного обучения, и не только в машинном обучении, но и в большей степени специализированных в области байесовского вывода.
Тогда у вас есть шанс правильно и без ошибок написать в этой модели код вывода, который действительно будет делать то, что вы думаете.
Соответственно, это существенно усложняет экспериментирование.
Например, запрос одной модели займет несколько недель, и неизвестно, получится или нет. Что уж говорить о том, чтобы попробовать несколько альтернативных моделей – мало у кого на это хватает терпения и сил.
Существует тенденция, что мало кто готов пробовать сложные модели в своих задачах, поскольку, как правило, чем сложнее модель, тем сложнее код вывода, и его мало кто может написать.
Поэтому все ограничиваются простыми моделями.
Однако очень часто более сложные модели обладают большей предсказательной силой, и потенциально от их использования можно получить большую прибыль.
Ученые задумались, как справиться с этой проблемой, и в качестве одного из решений была предложена такая парадигма, как вероятностное программирование.
Эта парадигма основана на двух идеях.
Во-первых, вам не следует писать код вероятностного вывода самостоятельно.
Это сложно и лучше оставить экспертам.
Все, что вам нужно сделать, это указать вероятностные модели, скажем, что вы наблюдали апостериорные распределения тех переменных в вашей модели, которые вас интересуют. Затем черный ящик, механизм вероятностного вывода, должен сделать вывод за вас.
Вторая идея заключается в том, что мы хотим, чтобы как можно больше людей извлекли выгоду из возможностей вероятностного моделирования.
Нам нужен способ формального описания вероятностных моделей, чтобы, с одной стороны, машина вероятностного вывода могла их понять, а с другой стороны, чтобы им могло пользоваться достаточно большое количество людей.
Какие формальные языки вообще известны подавляющему большинству людей, которые могли бы этим заниматься? Это языки программирования.
Идея вероятностного программирования заключается в следующем.
Вы описываете вероятностную модель с помощью программы, которая фактически реализует вашу модель физического процесса.
То есть это программа, которая, условно говоря, принимает на вход или генерирует в самом начале свойства интересующих вас объектов, а затем по некоторому алгоритму генерирует наблюдаемые данные, периодически обращаясь к датчику случайных чисел для добавления там немного шума.
Такая программа задает вероятностную модель, задает совместное распределение, а движок может анализировать программу и понимать, как сделать вывод. Наверное, это звучит немного утопично, но на данный момент действительно существует ряд движков, которые, возможно, не всегда и не для всех моделей работают, но позволяют делать выводы в интересных моделях среднего и высокого уровня сложности.
Некоторые из них перечислены на этом слайде.
Как выглядит вероятностная программа? Давайте сначала рассмотрим очень простой и с практической точки зрения бесполезный пример, который, однако, проиллюстрирует концепции, о которых мы говорим.
Модель очень проста: мы подбрасываем две монеты, смотрим, упадут ли они орлом или решкой, а затем посмотрим, выпадут ли они орлом или решкой вместе или нет. Как определить такую модель с помощью программы? Сначала мы создадим логическую переменную для каждой монеты.
Эти переменные примут значение «истина», если монета выпадет орлом, и «ложь», если монета выпадет решкой.
И давайте создадим еще одну переменную, которая будет принимать значение «истина» только тогда, когда обе монеты упадут орлом.
Функция, называемая здесь «Выборка Бернулли», представляет собой просто вызов генератора случайных чисел, который генерирует выборку из распределения Бернулли с учетом параметра 0,5. То есть эта функция вернет значение «истина» с вероятностью 0,5 и вернет значение «ложь» с вероятностью 0,5. Ее вызов эквивалентен подбрасыванию монеты.
Вот наша модель — теперь мы можем сделать несколько запросов к этой модели.
Вероятностный программный код, который будет показан, представляет собой некоторый псевдокод, который на самом деле не соответствует коду ни одной из обсуждаемых машин вероятностного вывода.
Поскольку синтаксис этих движков не предназначен для показа на слайдах и очень затрудняет понимание материала, но весь показанный код легко переносится на существующие движки без особых усилий и изменений этого кода, это чисто автоматическое и синтаксическое преобразование.
Вернемся к программе.
Мы можем задать какой-то запрос к этой модели.
Например, мы можем сказать, что мы заметили, что обе головы являются ложными, что означает, что обе монеты не выпали орлом.
Теперь мы можем спросить: какова вероятность того, что первая монета упадет орлом? Какой ответ должна дать в этом случае машина вероятностного программирования? В нашем процессе есть четыре конфигурации орла и решки.
Мы знаем, что конфигурация орел-орёл исключена, а в оставшихся трёх конфигурациях только одна из них имеет орёл, приземляющийся первым, правда.
Правильный ответ, который должен дать любой механизм вероятностного программирования в этом случае, заключается в том, что апостериорное распределение на coin1Heads представляет собой распределение Бернулли со значением параметра 1/3. С вероятностью 1/3 – орел, 2/3 – решка.
Очень простая вероятностная программа.
Какова семантика этих программ, как о них можно думать? Вы можете себе представить, что мы берём эту программу и запускаем её бесконечное количество раз, каждый раз обращаясь к генератору случайных чисел, генерирующему числа из некоторого распределения, и у нас есть ещё два оператора: infer — позволяет задавать вопросы, Observe — говорит, что мы знаем.
Идея в том, что когда мы запускаем эту программу бесконечно, каждый раз, когда мы доходим до оператора infer, она где-то сохраняет текущее значение переменной и, условно говоря, запоминает все значения переменной, чтобы, когда вы ее зададите, вернуть распределение ко всем значениям.
А оператор наблюдения смотрит, равно ли значение переменной в текущем выполнении программы тому, чему оно должно быть равно.
А если оно не равно, то прерывает текущее выполнение программы и сообщает всем операторам вывода, что в этом раунде не нужно было ничего запоминать, выбрасывайте все это, это плохое выполнение, не соответствует известным ограничениям нам.
На самом деле ни одна машина вероятностного вывода не работает таким образом.
Это было бы крайне неэффективно, но именно так и следует об этом думать.
Фактически такая программа задает совместное распределение значений всех переменных в этой программе, если рассматривать все бесконечные множества выполнений программы.
Исключив все те выступления, которые не соответствуют ограничениям.
Давайте рассмотрим не очень практичный, но уже более сложный пример вероятностной программы.
А именно, такая простая модель, как линейная регрессия.
Давайте посмотрим, как это можно написать на вероятностном языке программирования.
Что такое линейная регрессия? У нас есть некая наблюдаемая величина, и мы считаем, что она зависит от некоторых характеристик примерно линейно.
Характеристики (они же особенности): допустим, у нас есть несколько точек, каждая из них имеет вектор признаков, линейно влияющих на наблюдаемое значение.
То есть мы вычисляем его скалярное произведение с определённым вектором весов, добавляем немного шума, чтобы эта линейная зависимость была не точной, а приближенной.
И так мы получаем наблюдаемое значение.
Как это написать на вероятностном языке программирования? Для начала объявим массив признаков, который здесь обозначен X, — это двумерный массив, где объекты нашей выборки располагаются по первому измерению, а значения признаков — по второму.
второй.
Этот массив всегда доступен для наблюдения; мы можем, например, всегда вызвать функцию GetFeatures, которая считывает ее из файла, как в обычном программировании.
Теперь нам нужен вектор весов, реальные параметры этой модели.
Это случайная величина, и мы присвоим ей нормальное априорное распределение.
Как? Мы просто сгенерируем все веса из нормального распределения с ожиданием 0 и дисперсией 1, вызвав функцию, которая просто генерирует число из распределения с заданными параметрами.
Итак, по сути, задано априорное распределение — мы просто пишем код, который генерирует из него.
Теперь давайте создадим вектор Y для значения регрессии и заполним его.
Его значения равны скалярному произведению вектора весов и вектора признаков плюс некоторый случайный шум.
Строка Y[n] инициализирует значение Y случайным шумом с ожиданием 0 и дисперсией 0,1, а затем этот цикл добавляет к значению, которое мы инициализировали, скалярное произведение вектора признаков соответствующего объекта с вектором веса.
Теперь мы можем сказать, что наблюдали значения Y, читая их из файла или чего-то еще, и спросить у механизма вероятностного программирования, каково апостериорное распределение по W, если Y известно.
Это была пара простых примеров, призванных проиллюстрировать концепцию.
Теперь перейдем к интересным примерам — что можно легко сделать с помощью вероятностного программирования? Во-первых, давайте посмотрим на модель True Skill. Эта модель нужна, если у вас есть некая игра двух игроков, в которой исходом является либо первый, либо второй.
Здесь также содержатся результаты многих игр между игроками, и теперь вам хочется кое-что понять об игроках.
Например, вы хотите понять уровень навыков игроков или вы хотите посчитать вероятность того, что первый игрок победит второго, для двух игроков, которые никогда не играли вместе.
Зачем вообще это считать? Очевидные применения: спортивная аналитика или игровые сервисы, например онлайн.
В частности, модель True Skill впервые была придумана Microsoft для Xbox Live, потому что в Halo при автоматическом выборе, кто с кем играть, нужно было следить за тем, чтобы игроки были примерно одного уровня, иначе никто бы не интересовался играю.
Кроме того, с помощью таких игровых моделей можно моделировать совершенно неигровые ситуации.
В частности, в веб-поиске аналогичные модели используются для определения релевантности документов.
Когда, например, у нас есть сигнал о том, что кто-то сказал, что из данной пары документов при каких-то условиях этот лучше, а из данной пары лучше этот, мы всегда можем выделить, учесть и понять.
эти сигналы, какой документ действительно был лучшим, какой не очень и т. д. Поэтому такие модели важно знать и полезно изучать.
Одной из моделей решения этой проблемы является True Skill. Это очень просто, но удивительно мощно.
Идея такая: давайте опишем каждого игрока одним числом, показывающим его мастерство.
Чем выше число, тем лучше играет игрок, и наоборот. Когда два игрока собираются вместе и играют в игру, как мы определяем, кто выиграл, а кто проиграл? Мы возьмем мастерство игроков, добавим к нему немного шума, чтобы даже когда первый игрок заведомо сильнее второго, он с некоторой вероятностью все равно мог ему проиграть.
Чтобы наша модель могла генерировать все возможные результаты, а не только строго транзитивные, потому что в реальных данных этого не произойдет. Как эту идею можно реализовать на вероятностном языке программирования? Давайте создадим четыре массива.
В первом будут записываться навыки каждого игрока, а в трех других массивах описываются игры, в которые играют все игроки.
Для простоты пронумеруем игроков от 0 до PlayerCount-1, а игры от 0 до GameCount-1. Во втором массиве в соответствующей игре напишем, кто играл первым игроком, какой идентификатор у первого игрока от 0 до PlayerCount-1. В третий массив мы запишем все для второго игрока соответственно, а в четвертый напишем значение, истинное, если первый игрок выиграл соответствующую игру, и ложное, если выиграл второй игрок.
Теперь нам нужно установить априорные распределения для этих переменных.
В частности, предположим, что мы просто генерируем навыки из нормального распределения с центром в нуле и с единичной дисперсией.
Другими словами, априори все обладают примерно одинаковыми навыками, и очень большие отклонения в сторону очень хороших или плохих навыков маловероятны, поскольку нормальное распределение имеет довольно легкие хвосты.
Теперь мы можем генерировать результаты игры.
Для каждой игры берем игрока, который был в ней первым, игрока, который был вторым, и считаем, насколько навыки первого игрока превосходят навыки второго.
Мы получаем некоторое преимущество первого над вторым.
Теперь мы «зашумляем» это преимущество, добавляя к нему обычный шум с нулевым математическым ожиданием и небольшой дисперсией — так, чтобы тот, кто сильнее, скорее всего, выиграл, но мог и проиграть.
Первый игрок выигрывает, если это шумное преимущество больше нуля.
В противном случае выигрывает второй игрок.
Вероятностная модель задана, и теперь мы можем говорить о результатах игр и о том, какими навыками обладали игроки.
И получить апостериорное распределение по навыкам.
С этой моделью можно делать довольно интересные вещи.
В частности, Microsoft Research выпустила модификацию под названием True Skill Through Time. По сути та же модель, но теперь навыки игроков могут меняться каждый год. То есть каждый год к навыку добавляется какой-то нормальный шум с нулевым математическим ожиданием и небольшой дисперсией — навык может «плавать» во времени.
Затем взяли историю шахматных матчей ХХ века, применили к ней этот алгоритм и сравнили всех шахматных гроссмейстеров ХХ века.
Даже те, кто никогда не играл вместе.
Этот график из статьи.
Еще одна интересная модель – DARE. Какую проблему решает эта модель? Представьте себе, что у вас есть некий тест, в нем ряд вопросов, на каждый вопрос есть ряд возможных ответов, и у вас много студентов, которые прошли этот тест, ответили на вопросы, но вы не знаете правильных ответов.
на вопросы.
Однако вы хотите понять, какие ученики ответили правильно, а какие нет, и какие ответы были правильными.
Зачем решать такую проблему? Существует область, которая особенно актуальна для задач веб-поиска, называемая краудсорсингом.
Есть площадки, куда приходят люди, желающие подзаработать, и Яндекс дает им простые задания.
Например, скажите, имеет ли документ отношение к запросу или нет, есть ли на изображении собака и т. д. Проблема в том, что не все люди, которые приходят на эти площадки, могут хорошо ответить на поставленные вопросы.
Особенно, если вопросы не такие тривиальные, как наличие или отсутствие животного на изображении.
Кроме того, многие из них пытаются хитрить.
Например, отвечать наугад. Бывает, что сначала отвечают нормально, но потом устают. В результате мы имеем большое количество очень шумных ответов, многие из которых неверны.
И мы не знаем, какие из них правильные, иначе мы бы не отправляли эти задания на оценку.
И здесь нужны модели, которые позволят среди этого большого количества не всегда правильных ответов однозначно или с некоторым допущением определить правильные.
Условно говоря, по каждой фотографии можно сказать, что, исходя из наблюдаемых данных, существовала вероятность 0,7, что там был кот. Как решить такую проблему? В литературе предложено достаточно много моделей: Whitehil, BCC, DARE. Допустим, каждый ученик описывается одной цифрой – его способностями.
Чем выше его способности, тем выше вероятность того, что он правильно ответит на вопрос и наоборот. Каждый вопрос описывается двумя числами.
Во-первых, по сложности – чем она больше, тем меньше вероятность при прочих равных условиях, что ученик правильно ответит на вопрос.
Во-вторых, дискриминация – отличительность.
Если дискриминация вопроса высокая, то умения учащегося влияют на ответ на вопрос, а если низкая, то нет. То есть можно представить вопрос, который был плохо сформулирован, и было непонятно, о чем идет речь.
А хороший ученик или плохой – в конце концов вам придется прибегнуть к практически случайному гаданию.
Параметр дискриминации предназначен для моделирования таких ситуаций.
Какая вероятностная программа подойдет для этой модели? Во-первых, нам нужно сгенерировать все параметры модели из соответствующих априорных распределений.
Допустим, мы генерируем способности каждого ученика на основе нормального распределения с центром в нуле и некоторой дисперсии.
То есть мы говорим, что способности у всех примерно одинаковые, и крайние отклонения в сторону очень хороших и очень плохих от средних способностей маловероятны.
Для каждого вопроса мы генерируем его сложность из одного и того же распределения — сложность и способности расположены примерно на одной шкале.
А различительную способность мы генерируем из гамма-распределения, в том числе по определённым техническим причинам.
Гамма-распределение представляет собой распределение по положительной оси.
То есть дискриминация принимает значения больше нуля.
При этом он имеет среднее значение 1 и небольшую дисперсию.
Мы не знаем истинных ответов, поэтому генерируем их, так сказать, бросая игральную кость, у которой столько сторон, сколько возможных ответов на вопрос.
Теперь нам нужно описать процесс ответа учащихся на вопрос.
Для каждого ученика и для каждого вопроса мы сначала, как и в модели True Skill, вычисляем преимущество ученика над вопросом — то есть насколько способности ученика превышают сложность вопроса.
Теперь мы зашумили это преимущество следующим образом: чем больше дискриминационная сила вопроса о различении, чем меньше мы зашумляем это преимущество, тем больше соотношение способностей и сложности действительно повлияет на ситуацию.
Для этого мы используем функцию, которая генерируется из распределения с заданным математическим ожиданием и точностью.
Точность — это величина, обратно пропорциональная дисперсии.
Соответственно, чем больше дискриминации, тем меньше дисперсия и наоборот. Один пример из статьи про DARE. Мы взяли ответы учеников на IQ-тест и запустили модель DARE, которая не знает правильных ответов, а пытается их угадать и вычислить IQ каждого ученика.
И посчитали честный IQ. Если бы модель работала идеально, то все точки располагались бы на черной линии.
По осям: по вертикали – прогнозируемый моделью IQ, по горизонтали – реальный IQ. Но, как видите, они расположены вдоль прямой линии, то есть модель достаточно хорошо понимает, что происходит, хотя и ничего о происходящем не знает. Почему DARE работает? Если вы посмотрите, как работает вероятностный вывод в этой модели, и попытаетесь построить некую интуицию, вы обнаружите, что вывод работает примерно так.
Сначала мы рассмотрим тот факт, что если многие студенты ответили на вопрос одинаково, то, вероятно, все они ответили на него правильно, и этот вопрос прост. Если студент, ответивший на многие вопросы так же, как и остальные, ответил на эти вопросы, то этот студент, вероятно, знает, что делает, и обладает высокими способностями.
Тогда нам нужно присмотреться к остальным ответам этого ученика, в которых мы не так уверены – скорее всего, он тут как тут. Соответственно, если на какой-то вопрос плохой и хороший ученик отвечают на один и тот же вопрос, то, вероятно, у него достаточно низкая дискриминация.
И поэтому мы итеративно повторяем это рассуждение много раз, пока наши апостериорные распределения больше не перестанут меняться с использованием этой логики.
Модели просмотра результатов поиска.
Задача: у поисковых систем есть много информации о том, что мы показывали пользователям, куда они кликали, а куда нет, и мы хотим что-то понять об этих пользователях — что их интересовало, показывали ли мы им хорошие или плохие результаты.
.
Затем у нас есть задача изучить формулу ранжирования.
То есть обучение тех самых моделей, которые из двух миллионов результатов, найденных по вашему запросу, должны понимать, какие десять нужно показать.
Для обучения таких моделей необходимо много данных о том, какой документ какому запросу соответствует, а какой неактуален (обучающий набор).
У нас есть специальные люди – асессоры.
Их задача — сидеть весь день и отвечать на заданные пары документ-запрос по сложным инструкциям независимо от того, соответствует ли документ запросу или нет. Но работа оценщиков стоит денег; нанять их в большом количестве сложно, так как это будет довольно дорого.
А если для таких сложных задач использовать краудсорсинговые платформы, то получается, что задачи оказываются непомерно сложными для людей, которые туда приходят. Они просто не следуют таким инструкциям, и в итоге это очень похоже на случайное угадывание.
Тут возникает другая идея: если у нас есть клики пользователей на то, что мы им уже показали, то, может быть, по этим кликам мы сами сможем реконструировать, какие документы были релевантны, а какие нет, и использовать это для обучения наших формул ранжирования? Они решают эту проблему, моделируя каким-то образом то, как пользователь видит результаты.
Сделать это можно множеством способов разной степени сложности.
Здесь показан довольно простой метод, который, тем не менее, кое-где используется, например в Яндексе.
Это идея.
Пользователь просматривает результаты сверху вниз.
Итак он взял какой-то документ, и теперь ему нужно решить, кликать на этот документ или нет. Его решение зависит от того, насколько привлекательно краткое описание документа, которое находится на странице результатов поиска.
Даже если документ актуален, но описание не очень хорошее, пользователь никогда не узнает, что документ актуален, и не перейдет туда.
В этой модели пользователь сначала смотрит описание и, если оно ему не нравится, с некоторой вероятностью он решает просмотреть еще документы и перейти к следующим, и с некоторой вероятностью окажется, что он получает устает, разочаровывается в наших поисках и идет в Google. Если пользователь решает нажать на документ, то в этой модели он заходит, смотрит веб-страницу и решает, актуален документ или нет. Эта переменная сообщает, был ли документ релевантным.
Если документ был релевантным, то пользователь в некоторой степени удовлетворен этим документом и говорит, что завершил и удовлетворил свою информационную потребность, и с некоторой вероятностью проходит этот цикл еще раз и просматривает следующий документ. А если следующий документ оказался неактуален, то он снова может решить посмотреть еще раз или закончить.
Такие модели используются в некоторой модификации.
Здесь было бы слишком много кода, чтобы показать программы, но принцип понятен, как можно написать нечто подобное.
Как мы это применяем.
Если клики есть, то можно понять релевантность и привлекательность сниппетов.
Еще один интересный пример.
Допустим, у нас есть запрос, и на его основе мы показываем некий набор документов.
И вообще, было бы неплохо, чтобы у нас была какая-то метрика, которая говорит, хорош наш поиск или плох — некая цифра, которую мы можем отслеживать с течением времени и стараться всячески ее увеличивать.
Очень удобно иметь такой номер.
Как его построить? В качестве метрики можно использовать вероятность того, что среднестатистический пользователь удовлетворен результатами, и чем больше эта вероятность, тем лучше все работает. Как вычислить значение этой вероятности? Можно использовать ту же модель - рассчитывать ее параметры (вероятность устать, вероятность зайти в гугл и т.д.) можно либо по кликам, либо, что еще лучше, по реальной разметке ассессора, чтобы значения параметров были лучше.
и разница меньше.
А потом использовать это как формулу для расчета какой-то целевой метрики, которую мы отслеживаем в поиске.
Это еще один способ применения этой модели.
Вероятностное моделирование часто бывает довольно сложным, поскольку вам нужно уметь писать код вероятностного вывода.
Разбираться в этом интересно, но делать это постоянно не хочется.
и вероятностный Теги: #Машинное обучение #математика #программирование #Яндекс #Поисковые технологии #вероятностное программирование #Байесовский вывод
Введение Данная публикация представляет собой первую часть краткого введения с иллюстрациями к вероятностное программирование , которое является одной из современных прикладных областей машинного обучения и искусственного интеллекта.
Во время написания этой публикации я был рад обнаружить, что совсем недавно я уже посещал Хабрахабр.
статья о вероятностном программировании с рассмотрением прикладных примеров из области когнитивной теории , хотя, к сожалению, в русскоязычном Интернете пока мало материалов на эту тему.
Я, автор Юра Перов, уже два года занимаюсь вероятностным программированием в рамках своей основной образовательной и научной деятельности.
Плодотворное знакомство с вероятностным программированием у меня произошло, когда, будучи студентом Института математики и фундаментальной информатики Сибирского федерального университета, я проходил стажировку в Лаборатории компьютерных наук и искусственного интеллекта Массачусетского технологического института под руководством профессора Джошуа.
Тененбаум и доктор Викаш Мансингха, а затем продолжил на факультете инженерных наук Оксфордского университета, где в настоящее время учусь в магистратуре под руководством профессора Фрэнка Вуда.
Мне нравится определять вероятностное программирование как компактный , композиционный метод представления генеративные вероятностные модели и проведение статистические выводы в них с учетом данных с использованием обобщенных алгоритмов.
Хотя вероятностное программирование не привносит много фундаментального нового в теорию машинного обучения, этот подход привлекателен своей простотой: «вероятностные генеративные модели для масс!»
«Обычное» программирование
Чтобы познакомить вас с вероятностным программированием, давайте сначала поговорим об «обычном» программировании.В «обычном» программировании основой является алгоритм, обычно детерминированный, позволяющий получать выходные данные из входных данных по четко установленным правилам.
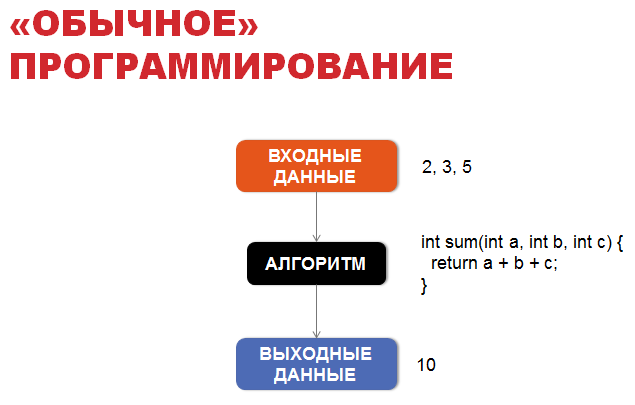
Например, если у нас есть мальчик Вася, и мы знаем, где он находится, куда бросает мяч и каковы внешние условия (например, сила ветра), мы будем знать, какое окно в здании школы он, к сожалению, разобьет. Для этого достаточно смоделировать простые законы школьной физики, которые легко записать в виде алгоритма.

А теперь вероятностное программирование
Однако зачастую мы знаем только результат, итог, и нам интересно знать, какие неизвестные значения привели к этому конкретному результату? Для ответа на этот вопрос с помощью теории математического моделирования создается вероятностная модель, некоторые параметры которой точно не определены.
Например, в случае мальчика Васи, зная, какое окно он разбил, и имея априорные знания о том, возле какого окна он и его друзья обычно играют в футбол, и зная прогноз погоды на этот день, мы хотим знать апостериорное распределение местонахождения мальчика Вася: откуда он бросил мяч? 
Итак, зная выходные данные, нас интересует наиболее вероятные значения скрытых, неизвестных параметров.
В рамках машинного обучения мы также рассматриваем создание вероятностные модели.
В рамках генеративно-вероятностных моделей модель описывается как алгоритм, но вместо точных однозначных значений скрытых параметров и некоторых входных параметров мы используем вероятностные распределения по ним.
Существует более 15 языков вероятностного программирования, список с кратким описанием каждого из них можно найти здесь.
Здесь .
В этой публикации приведен пример кода на вероятностных языках.
Риск / англиканский , которые имеют очень похожий синтаксис и происходят из вероятностного языка Церковь .
Чёрч, в свою очередь, основан на «обычных» языках программирования Lisp и Scheme. Заинтересованному читателю настоятельно рекомендуется прочитать книгу.
«Структура и интерпретация компьютерных программ» , что является одним из лучших способов начать работу с «обычным» языком программирования Scheme.
Пример байесовской линейной регрессии
Давайте рассмотрим задание простой вероятностной модели байесовской линейной регрессии на языке вероятностного программирования Venture/Anglican в виде вероятностной программы:Скрытые обязательные параметры - значения коэффициентов т1 И т2 линейная функция х = t1 + t2 * время .01: [ASSUME t1 (normal 0 1)] 02: [ASSUME t2 (normal 0 1)] 03: [ASSUME noise 0.01] 04: [ASSUME noisy_x (lambda (time) (normal (+ t1 (* t2 time)) noise))] 05: [OBSERVE (noisy_x 1.0) 10.3] 06: [OBSERVE (noisy_x 2.0) 11.1] 07: [OBSERVE (noisy_x 3.0) 11.9] 08: [PREDICT t1] 09: [PREDICT t2] 10: [PREDICT (noisy_x 4.0)]
Имеем априорные предположения об этих коэффициентах, а именно предполагаем, что они распределены по закону нормального распределения.
Нормальный(0, 1) со средним значением 0 и стандартным отклонением 1. Таким образом, в первых двух строках вероятностной программы мы определили априорную вероятность для скрытых переменных, П(Т) .
инструкции [ПРЕДПОЛАГАЕТ выражение имени] можно рассматривать как определение случайной величины с именем имя , принимая значение вычисляемого выражения (программного кода) выражение , который содержит неопределенность.
Вероятностные языки программирования (имеются в виду, в частности, Church, Venture, Anglican), такие как Lisp/Scheme, являются функциональными языками программирования и используют польскую нотацию при написании выражений для вычислений.
Это значит, что в выражении вызова функции первым ставится оператор, а уже потом аргументы: (+ 1 2) , а вызов функции заключен в круглые скобки.
В других языках программирования, таких как C++ или Python, это было бы эквивалентно коду 1 + 2 .
В языках вероятностного программирования выражения вызова функций обычно делятся на три разных типа:
- Вызов детерминированных процедур (примитивная процедура arg1… argN) , которые при одних и тех же аргументах всегда возвращают одно и то же значение.
К таким процедурам, например, относятся арифметические операции.
- Вызов вероятностных (стохастических) процедур (стохастическая процедура arg1… argN) , которые при каждом вызове случайным образом генерируют элемент из соответствующего распределения.
Этот вызов определяет новый случайная переменная .
Например, вызов вероятностной процедуры (нормальный 1 10) определяет случайную величину, распределенную по закону нормального распределения Нормальный(1, sqrt(10)) , и результатом выполнения каждый раз будет какое-то действительное число.
- Вызов составных процедур (составная процедура arg1… argN) , Где составная процедура — процедура, вводимая пользователем с использованием специального выражения лямбда : (лямбда (arg1… argN) тело) , Где тело — тело процедуры, состоящее из выражений.
В общем, составная процедура является стохастической (недетерминированной) составной процедурой, поскольку ее тело может содержать вызовы вероятностных процедур.
После первых двух строк мы хотим установить условную вероятность Р(Х | Т) , то есть условная вероятность наблюдаемых переменных х1 , х2 , х3 для заданных значений скрытых переменных т1 , т2 и параметр время .
Прежде чем вводить сами наблюдения, используя выражение [НАБЛЮДАТЬ.
] мы определяем общий закон для наблюдаемых переменных xi в рамках нашей модели, а именно, мы предполагаем, что эти наблюдаемые случайные величины для заданных т1 , т2 и заданный уровень шума шум распределяется по закону нормального распределения Нормальный(t1 + t2 * время, sqrt(шум)) со средним t1 + t2 * время и стандартное отклонение шум .
Эта условная вероятность определяется в строках 3 и 4 этой вероятностной программы.
шумный_x определяется как функция, принимающая параметр время и возвращаем случайное значение, определенное путем оценки выражения (нормальный (+ t1 (* t2 время)) шум) и обусловлено значениями случайных величин т1 И т2 и переменная шум .
Обратите внимание, что выражение (нормальный (+ t1 (* t2 время)) шум) содержит неопределенность, поэтому каждый раз, когда мы его вычисляем, мы обычно получаем другое значение.
В строках 5-7 непосредственно вписываем известные значения х1 = 10,3 , х2 = 11,1 , х3 = 11,9 .
Инструкция формы [значение выражения НАБЛЮДАТЬ] фиксирует наблюдение, что случайная величина принимает значение в соответствии с выполнением выражения выражение , взял значение ценить .
Давайте повторим на этом этапе все, что мы сделали.
В строках 1-4, используя такие инструкции, как [ПРЕДПОЛАГАТЬ.
] мы непосредственно указали саму вероятностную модель: П(Т) И Р(Х | Т) .
В строках 5-7 мы непосредственно указали значения известных нам наблюдаемых случайных величин.
Икс используя такие инструкции, как [НАБЛЮДАТЬ.
] .
В строках 8-9 мы запрашиваем у системы вероятностного программирования апостериорное распределение.
Р(Т | Х) скрытые случайные величины т1 И т2 .
Как уже говорилось, при большом объеме данных и достаточно сложных моделях невозможно получить точное аналитическое представление, поэтому инструкции вида [ПРЕДСКАЗЫВАТЬ.
] сгенерировать выборку значений случайной величины из апостериорного распределения Р(Т | Х) или его подход. Инструкция формы [выражение ПРЕДСКАЗАНИЕ] в общем случае генерирует один элемент выборки из значений случайной величины, принимающей значение в соответствии с выполнением выражения выражение .
Если перед такими инструкциями, как [ПРЕДСКАЗЫВАТЬ.
] инструкции по форме [НАБЛЮДАТЬ.
] , то выборка будет из апостериорного распределения (точнее, конечно, из аппроксимации апостериорного распределения), обусловленного ранее введенными перечисленными наблюдениями.
Обратите внимание, что в конце мы также можем предсказать значение функции х(время) в другом месте, например, в время = 4,0 .
В этом случае прогнозирование означает создание выборки из апостериорного распределения новой случайной величины с учетом значений скрытых случайных величин.
т1 , т2 и параметр время = 4,0 .
Чтобы создать выборку из апостериорного распределения Р(Т | Х) в языке программирования Venture в качестве основного используется алгоритм Метрополиса-Гастингса, который относится к методам Монте-Карло по схеме цепи Маркова.
Под обобщенный Вывод в данном случае означает, что алгоритм может быть применен к любым вероятностным программам, написанным на данном языке вероятностного программирования.
В прикрепленном ниже видео вы можете увидеть статистические выводы, происходящие в этой модели.
(В видео показан пример на основе вероятностного языка программирования Venture.) В самом начале у нас нет данных, поэтому мы видим априорное распределение линий.
Добавляя по точкам (таким образом, элементы данных), мы видим элементы выборки из апостериорного распределения.
На этом завершается первая часть введения в вероятностное программирование.
Материалы
Ниже приведены некоторые рекомендуемые ссылки для тех, кто хочет узнать больше о вероятностном программировании прямо сейчас:- Сайт вероятностного языка программирования Anglican, брата Venture и потомка Church. .
- Курс обучения английскому вероятностному языку программирования .
- Курс по вероятностному программированию, преподаваемый в одной из школ машинного обучения: часть 1 , часть 2 И часть 3 .
- Курс «Проектирование и реализация вероятностных языков программирования» .
- Курс «Вероятностные генеративные модели познания (одна из областей применения вероятностного программирования)» .
Заинтересованный читатель найдет в ней более подробное и формальное введение в вероятностное программирование.
В конце работы также содержится вся библиография, на основе которой написана данная публикация.
Теги: #Машинное обучение #вероятностное программирование #искусственный интеллект #программирование

-
Какой Домен Верхнего Уровня
19 Oct, 24 -
Взлом Базы Данных Из-За Lfi
19 Oct, 24 -
Амазонка: Вопросы И Ответы
19 Oct, 24 -
Золотые Медальоны
19 Oct, 24


