Мне когда-то понадобилось рассчитать изофоты (линии одинаковой интенсивности на изображениях), однако готовых библиотек я не нашел, а копаться в чужом коде (например, в том же Октаве или Ирафе) очень не хотелось.
.
В качестве простейшего алгоритма, который я нашел метод шагающего квадрата .
Однако этот метод сильно снижает пространственное разрешение при расчете узлов изофот, поэтому я решил его немного модифицировать и сделать квадраты перекрывающимися.
Первая реализация (кстати, довольно быстро) не удалось: т.к.
Я построил маску, общую для всех уровней, а для конкретного уровня пересчитал ее отдельно; в точках, через которые проходит несколько изолиний, имелись разрывы.
Ковыряние в коде приводило к появлению все большего количества взаимоблокировок и флагов, поэтому я решил пожертвовать производительностью и рассчитывать маски отдельно для каждого уровня интенсивности.
Итак, позвольте мне вкратце повторить, что такое метод «шагающих квадратов».
Построить изофоты уровня I я Сначала строится специальная маска: для каждого пикселя изображения кодируется относительное положение его «соседей» справа, снизу и справа снизу.
Это можно закодировать по-разному, я просто представил код в виде битовой маски 000abcd, где a,b,c и d — относительные интенсивности в соответствующих пикселях (a — наш текущий пиксель изображения).

Если значение в пикселе больше уровня изолинии, соответствующему биту присваивается единица; в противном случае ноль.
Если w — ширина изображения, а *in — указатель на пиксель a, то значение маски (*out) для этого пикселя вычисляется следующим образом:
В результате, в зависимости от конфигурации пикселя, мы получаем одно из 16 значений:*out = (unsigned char) ((in[0]>lvl)<<3) | ((in[1]>lvl)<<2) | ((in[w]>lvl)<<1) | (in[w+1]>lvl);
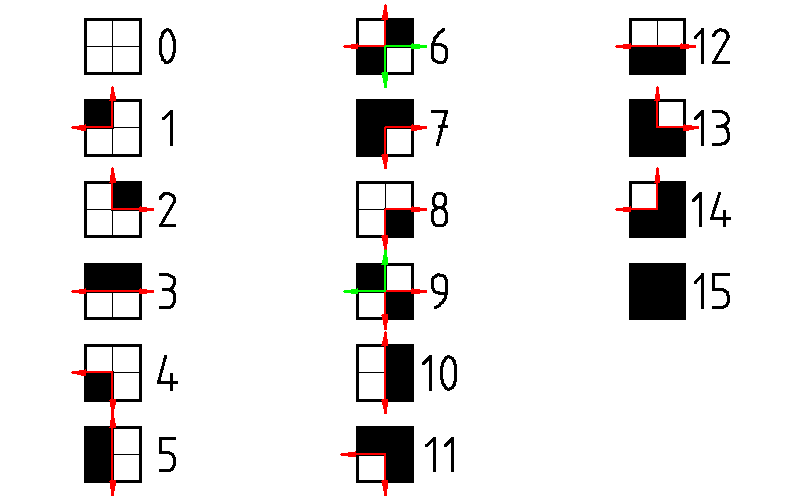
Размер маски в обоих измерениях на единицу меньше размера изображения.
Следующий шаг — проверка поочередно всех пикселей маски на неравенство между нулем и 15. Как только мы находим такой пиксель, начинаем строить по нему изолинию.
Чтобы правильно построить изолинии, нам необходимо запомнить направление, с которого мы подошли к данному пикселю.
На рисунке выше стрелками указаны возможные пути выхода из каждого пикселя маски.
Если мы не учтем запрещенное направление (откуда мы пришли), то нам придется либо проверять лишние пиксели маски, либо (в случае особых точек 6 и 9, но о них позже) мы можем совершенно неверно выбрать положение следующей точки изофоты.
Если мы просматриваем пиксели маски (слева направо и сверху вниз, если считать начало изображения в верхнем левом углу), пока не обнаружим только пустые ячейки, то «запрещенным» направлением является «левое» направление.
.
Как только мы находим ячейку, содержащую участок изолинии, мы в соответствии с заранее подготовленным массивом «направлений» выбираем следующее направление, отсекая «запрещенные».
Если таких направлений два, то выбираем вправо или вниз (с приоритетом «вправо») при движении по часовой стрелке и влево или вверх (с приоритетом «вверх») при движении против часовой стрелки (об этом позже).
После этого мы вычисляем положение узла изолинии для конкретного пикселя.
Это делается с помощью одной из функций массива в соответствии со значением маски в данном пикселе.
На рисунке ниже показано, как рассчитывается эта позиция.
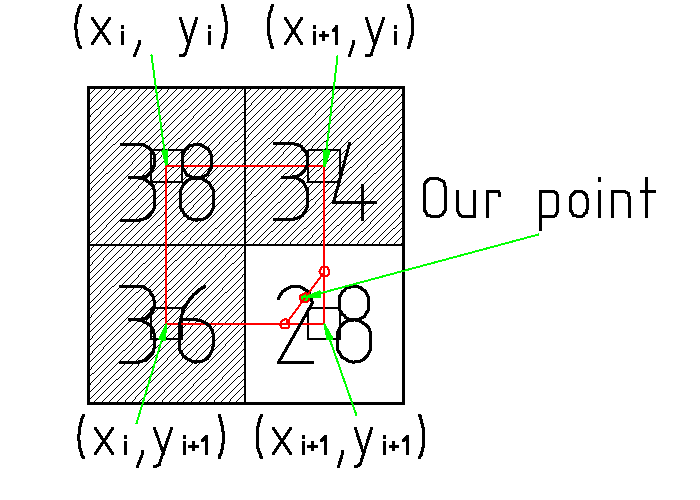
Итак, пусть изображение имеет интенсивности, показанные на рисунке (цифры внутри ячеек).
Изофоту проводим на уровне 30. Конфигурация соседей пикселей (x я , да я ) соответствует значению маски, равному семи.
Вызываем соответствующую функцию, которая с помощью линейной интерполяции вычисляет координаты опорных точек изолиний на прямых, соединяющих два правых пикселя по вертикали и два нижних по горизонтали.
Соответствующие точки отмечены незакрашенными красными кружками.
Соединив их прямой линией и найдя ее центр, мы получим искомый узел изофот (отмечен красным кружком с зеленой заливкой «Наша точка»).
Это, конечно, не очень правильный метод, но для большинства задач его достаточно.
Каждый узел добавляется в хвост соответствующего списка.
Как только соответствующее значение маски будет использовано, оно сбрасывается на ноль, и мы переходим к следующему соседнему пикселю маски.
Если его содержимое соответствует следующему узлу изофоты, продолжаем расчет, иначе «закрываем» изофоту.
Сразу после «замыкания» изофоты мы проверяем, во-первых, не слишком ли она коротка (скажем, в районе одного пикселя), а во-вторых, проверяем ее замыкание: лежат ли начало и конец изофоты не далее, чем, скажем, На расстоянии 2 пикселей мы считаем его закрытым.
Процедура «замыкания» изофоты заключается в проверке «на всякий случай», не продолжает ли изофота от своей первой точки в обратном направлении.
Для этого перемещаемся к нижнему пикселю маски от первого с запретом движения вверх.
Если мы находим там продолжение изофоты, то идем до ее конца, добавляя узлы в «голову» списка и выбирая приоритетными направления против часовой стрелки.
Все вышесказанное справедливо до тех пор, пока мы не «натолкнемся» на специальные пиксели: 6 и 9. Через эти пиксели маски проходят две изофотные линии, поэтому необходимо, исходя из «запрещенного» направления, выбрать правильное следующее направление.
Так, например, если мы «наткнемся» на цифру 6, идущую слева, следующим направлением будет «вверх».
Чтобы не «забыть» еще об одной точке изолинии при следующем проходе, заменяем специальное значение на «не специальное», просто «закрашивая» уже использованный пиксель (т.е.
, например, для случая попадания «шестерку» слева мы «закрашиваем верхний левый пиксель, т.е.
заменяем 6 на 7).
Этот метод, к сожалению, вызывает «промахи» в случае однопиксельных «провалов» в «горбах» интенсивности.
Но, к сожалению, исправление этого — очень сложная алгоритмическая задача, которая отнимет слишком много компьютерного времени для построения изофот. И для большинства изображений описанный метод прекрасно работает. Таким образом, «специальные» пиксели используются дважды, сбрасываясь только после второго прохода.
Расчет узлов в особых точках производится в обратном порядке: для этого берется функция, «закрашивающая» пиксель, противоположный используемому.
Работу алгоритма я проиллюстрирую на примере прохождения «пика» из двух пикселей, показанного на рисунке ниже.
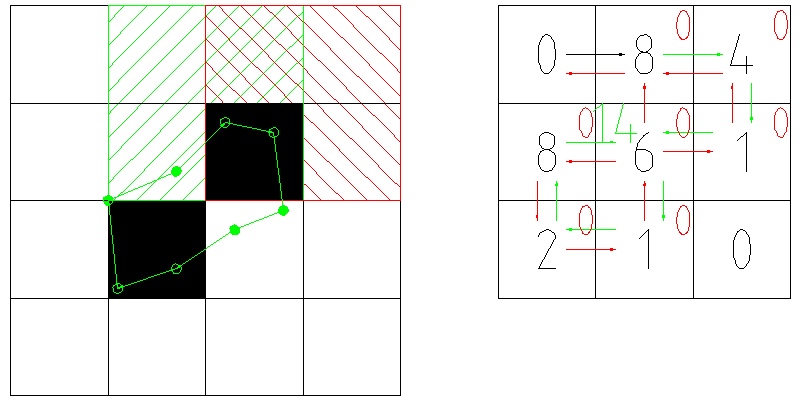
Данная область изображения размером 4х4 пикселя соответствует маске 3х3 пикселя (справа).
Начинаем движение с верхнего левого пикселя изображения.
Так как на маске ему соответствует ноль, то переходим к соседнему правому пикселю маски (помнив, что на «правом» направлении у нас «запрет»).
Запрещенные направления показаны на рис.
справа красными стрелками, «пустые» переходы — черной стрелкой, переходы с расчетом узлов изолиний — зелеными стрелками.
Итак, «натыкаемся» на восьмерку и используем соответствующую функцию для расчета положения первого узла изофоты.
Далее смотрим на заранее подготовленный массив и видим, что направление «вылета» от текущего пикселя либо «вправо», либо «вниз».
Выбираем «правое» направление и переходим к следующему пикселю (4), не забывая сбросить уже использованный пиксель маски (обнуление пикселей отмечается красными нулями в правом верхнем углу пикселя).
Далее переходим к значению 1, а после этого к специальной точке со значением 6. Поскольку мы пришли справа, то вычисляем значение узла с помощью функции для значения маски, равного семи, и заменяем шестерку на маска с 14. После этого спускаемся к единице.
После того, как мы пройдем один, два и восемь, мы вернемся к нашему «особому» пикселю, но там уже будет значение 14, т.е.
дальнейший расчет будет происходить «как ни в чем не бывало», после чего нам нужно будет двигаться вверх.
Однако наверху мы встречаем ноль.
В «голову» списка узлов мы также ничего добавить не можем, потому что значение под начальным пикселем изолинии также обнуляется.
Поэтому проверяем близость начального и конечного узлов линии.
Они расположены довольно близко, и мы можем отметить этот контур как замкнутый.
Все исходники алгоритма можно найти Здесь .
Также планирую добавить распараллеливание расчета изолиний разных уровней, чтобы запускать хотя бы 4.8 параллельных потоков.
Пока что в одном потоке для тестового изображения размером 3000х3000 пикселей построение изофот на 16 уровнях занимает около 1,2с.
Теги: #изолинии #изофоты #ходячие квадраты #Алгоритмы

-
Страх На Продажу: Тайна Поместья Макинроев
19 Oct, 24 -
Как Сдать Экзамен Istqb, Не Выходя Из Дома
19 Oct, 24 -
Apple Event Unleashed — Текстовая Трансляция
19 Oct, 24 -
Блеск И Нищета Российского Онлайн-Шопинга...
19 Oct, 24 -
Опубликован Топ-100 Студий От Tagline
19 Oct, 24


